Układ dwóch elektronów – Hamiltonian

Układ dwóch elektronów – Hamiltonian
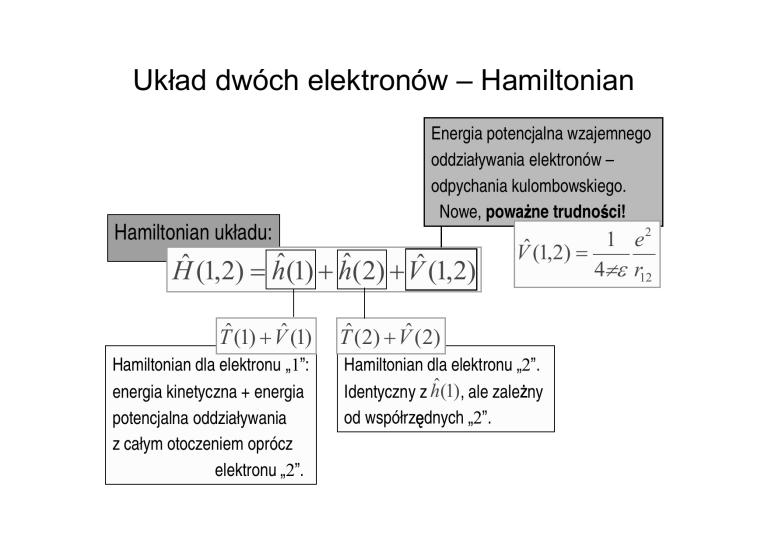
Energia potencjalna wzajemnego
oddziaływania elektronów –
odpychania kulombowskiego.
Nowe, powa ne trudno ci!
Hamiltonian układu:
Hˆ (1,2) = hˆ(1) + hˆ(2) + Vˆ (1,2)
Hamiltonian dla elektronu „1”:
energia kinetyczna + energia
potencjalna oddziaływania
z całym otoczeniem oprócz
elektronu „2”.
Tˆ (2) + Vˆ (2)
Hamiltonian dla elektronu „2”.
Identyczny z ĥ(1), ale zale ny
od współrz dnych „2”.
Tˆ (1) + Vˆ (1)
2
e
1
Vˆ (1,2) =
4πε r12
Układ dwóch elektronów
– przybli enie nieoddziałuj cych elektronów
Hamiltonian układu:
Hˆ (1,2) = hˆ(1) + hˆ(2) + Vˆ (1,2)
Pomijamy wzajemne oddziaływanie elektronów.
Jest to uzasadnione tylko wtedy, gdy energia ich
wzajemnego odpychania jest du o mniejsza od
energii potencjalnej jednoelektronowej (obu el.),
uwzgl dnionej w
Hamiltonian przybli ony
Hˆ o = hˆ(1) + hˆ(2)
przybli enie nieoddziałuj cych elektronów.
Nierelatywistyczny
– nie zawiera spinu.
Układ dwóch elektronów
– przybli enie nieoddziałuj cych elektronów
Trzeba rozwi za równanie
Hˆ o Ψ = EΨ
Hˆ o = hˆ(1) + hˆ(2)
Zmienne obu elektronów s od siebie odseparowane
w dwóch wyrazach Hamiltonianu. W takich przypadkach mo na znale rozwi zanie
równania własnego w postaci iloczynu
ϕ (r1 )ψ (r2 )
Taki iloczyn nie ma wła ciwej symetrii permutacyjnej, ale zajmiemy si tym pó niej.
[hˆ(1) + hˆ(2)]ϕ (r1 )ψ (r2 ) = Eϕ (r1 )ψ (r2 )
Dalej post pujemy tak jak zwykle przy separacji zmiennych.
Układ dwóch elektronów
– przybli enie nieoddziałuj cych elektronów
[hˆ(1) + hˆ(2)]ϕ (r1 )ψ (r2 ) = Eϕ (r1 )ψ (r2 )
1 ˆ
1 ˆ
h(1)ϕ (r1 ) = E −
h(2)ψ (r2 )
ϕ (r1 )
ψ (r2 )
hˆ(1)ϕ (r1 ) = ε 1ϕ (r1 )
ε1
hˆ(2)ψ (r2 ) = ( E − ε 1 )ψ (r2 )
Jest to w zasadzie jedno równanie – równanie Schrödingera dla jednego elektronu.
Zwykle umiemy takie równanie rozwi za . Załó my, e znamy rozwi zania:
hˆϕm = ε mϕm , m = 1,2,
E = εk + εn
W przybli eniu nieoddziałuj cych elektronów, energia dwuelektronowa jest sum energii poszczególnych elektronów, a odpowiadaj ca
jej funkcja falowa – iloczynem funkcji jednoelektronowych:
ϕk (r1 )ϕ n (r2 )
Układ dwóch elektronów
– przybli enie nieoddziałuj cych elektronów
Tej energii odpowiadaj dwie funkcje:
E = εk + εn
ϕk (r1 )ϕn (r2 ) ϕn (r1 )ϕk (r2 )
oraz dowolne ich kombinacje liniowe. W ród nich s równie te wła ciwe – antysymetryczne,
które mo na utworzy dopiero ze spinorbitali - po doł czeniu do orbitali wektorów spinowych.
k≠n
E = εk + εn
2 S +1
MS
Ψkn
Ogólne
oznaczenie.
k =n
singlet 10Ψkn = 12 (ϕkϕn + ϕnϕk )(αβ − βα )
Ψkn =
3
1
tryplet
E = 2ε k
1
2
(ϕkϕn − ϕ nϕk )αα
Ψkn = 12 (ϕkϕn − ϕnϕk )(αβ + βα )
3
0
Ψkn =
3
−1
Ψkk =
1
0
1
2
1
2
(ϕkϕn − ϕnϕk ) ββ
ϕkϕk (αβ − βα ) Tylko singlet.
Układ dwóch elektronów c.d
Wracamy do pełnego hamiltonianu z
oddziaływaniem mi dzyelektronowym.
Hˆ (1,2) = hˆ(1) + hˆ(2) + Vˆ (1,2)
Naszym celem jest znalezienie dozwolonych energii układu,
tzn. rozwi zanie równania Schrödingera H
ˆ Ψ = EΨ
E
E
Równania własnego dla pełnego hamiltonianu nie mo na rozwi za ci le.
W praktyce znajduje si przybli one rozwi zania:
przybli one funkcje i przybli one energie własne.
Układ dwóch elektronów c.d
W jakiej postaci poszukiwa rozwi zania równania
ĤΨ = EΨ
?
Ψ powinna by
antysymetryczna. W tym celu musi zawiera zmienne spinowe.
Jako „funkcja” spinowa mo e by funkcj własn operatorów kwadratu i rzutu
2 S +1
2
ˆ
ˆ
ˆ , S ] = 0, [ Hˆ , S ] = 0 . Wi c mo e to by M ΨE
całkowitego spinu, bo [ H
z
S
{ϕ (r )}
i
i∈I jest doskonstruowana z funkcji jednoelektronowych. Je li
woln baz w przestrzeni jednoelektronowej, to iloczyny ϕ k ( r1 )ϕ n ( r2 ) stanowi baz
w przestrzeni funkcji dwuelektronowych. Trzeba je jeszcze skojarzy ze wszystkimi mo liwymi wektorami spinowymi i antysymetryzowa – doprowadzi do postaci funkcji 2 S +1
Ψ mo e by
(patrz dwie strony wcze niej)
Ms
kn
I w takiej postaci mo na by go poszukiwa .
Ψkn
Niestety rozwini cie
jest niesko czone.
Konieczne s przybli enia
c
=
2 S +1
kn M S
Rozwi zanie r-nia Schrödingera
2 S +1
mo na ci le przedstawi jako M ΨE
S
Ψkn
Układ dwóch elektronów – przybli enie jednoelektronowe
Je li przybli enie nieoddziałuj cych elektronów nie było zupełnie bez sensu, to uwzgl dnienie pełnego hamiltonianu i przybli enie dwuelektronowej funkcji falowej przez jeden
wyraz rozwini cia (jedn par funkcji jednoelektronowych kn) powinno by lepsze.
Jest to przybli enie jednoelektronowe.
Przyporz dkowanie dwóm (N) elektronom pary (Nki) orbitali nazywa si konfiguracj dwu(N-) elektronow . Przybli enie jednoelektronowe mo na nazywa jednokonfiguracyjnym.
ckn 2 SM+1S Ψkn
ΨE =
kn
2 S +1
MS
ΨE ≈ 2 SM+1S Ψkn
przybli enie jednoelektronowe
2 S +1
MS
(
2 S +1
MS
2 S +1
ˆ
Ψkn , H M SΨkn )
Przybli ona energia odpowiadaj ca
takiej przybli onej funkcji jest warto ci oczekiwan energii.
Przekonamy si , e zale y nie tylko od pary kn funkcji
jednoelektronowych, lecz tak e od spinu, od liczby S.
Układ dwóch elektronów – przybli enie jednoelektronowe
S
2 S +1
2 S +1
Mamy przybli on funkcj M S Ψkn = Φ kn ( r1 , r2 ) χ M S
Obliczmy odpowiadaj c
2 S +1
ˆ 2 S +1Ψ ) =
E
=
(
Ψ
,
H
kn
M S kn
M S kn
jej energi
S
S
S
S
= (Φ kn
, Hˆ Φ kn
)( χ 2 SM+S1, χ 2 SM+S1) = (Φ kn
, Hˆ Φ kn
)
k≠n
Ekn =
{
S
Φ kn
=
(
1
ϕ kϕn + (−1) S ϕ nϕ k
2
)
[
=1
]
}
C
B
D
1 A
S
= (ϕ kϕ n , Hˆ ϕ kϕ n ) + (−1) (ϕ kϕ n , Hˆ ϕ nϕ k ) + (ϕ nϕ k , Hˆ ϕ kϕ n ) + (ϕ nϕ k , Hˆ ϕ nϕ k )
2
A = D i B = C bo Hˆ (r1 , r2 ) = Hˆ (r2 , r1 )
Ekn = (ϕ kϕ n , Hˆ ϕ kϕ n ) + (−1) S (ϕ kϕ n , Hˆ ϕ nϕ k )
Układ dwóch elektronów – przybli enie jednoelektronowe
E = (ϕ ϕ , Hˆ ϕ ϕ ) + (−1) S (ϕ ϕ , Hˆ ϕ ϕ )
kn
k
n
k
n
k
n
n
k
Hˆ (1,2) = hˆ1 + hˆ2 + Vˆ12
(ϕ kϕ n , (h1 + h2 + V12 )ϕ kϕ n ) = (ϕ k , h1ϕ k )(ϕ n ,ϕ n ) + (ϕ k ,ϕ k )(ϕ n , h2ϕ n ) +
e2
+
4
Całka kulombowska
1
= h k+ h n+
4
J kn
ϕ k* (r1 )ϕ n* (r2 )
1
ϕ k (r1 )ϕ n (r2 )dV1dV2 =
r12
e|ϕ k (r1 )|2e|ϕ n (r2 )|2
dV1dV2 = h k + h n + J kn
r12
(ϕ kϕ n , (h1 + h2 + V12 )ϕ nϕ k ) = (ϕ k , h1ϕ n )(ϕ n , ϕ k ) + (ϕ k , ϕ n )(ϕ n , h2ϕ k ) +
e2
1
*
*
+
ϕ k (r1 )ϕ n (r2 ) ϕ n (r1 )ϕ k (r2 )dV1dV2 =
r12
4πε
e2
1 *
*
Całka wymienna
=
ϕ k (r1 )ϕ n (r1 ) ϕ n (r2 )ϕ k (r2 )dV1dV2
K kn
r12
4πε
Układ dwóch elektronów – przybli enie jednoelektronowe
„Energie
jednoelektronowe”
„Energia
oddziaływania”
Ekn = h k + h n + J kn + (−1) S K kn
Efekt kulombowski
Efekt wymienny
Przybli ona energia układu dwuelektronowego odpowiadaj ca przybli onej funkcji 2 SM+1S Ψkn
skonstruowanej z pary ró nych orbitali ϕ k , ϕ n – zale y od kwadratu całkowitego spinu (S),
ale nie zale y od rzutu całkowitego spinu (MS).
Układ dwóch elektronów – przybli enie jednoelektronowe
2 S +1
MS
k=n
S
Ψkn = Φ kn
(r1 , r2 ) χ M2 SS+1
Mamy przybli on funkcj
Obliczmy odpowiadaj c
jej energi
Ekn =( 2 SM+1S Ψkn , Hˆ 2 SM+1SΨkn ) =
S
S
S
S
= (Φ kn
, Hˆ Φ kn
)( χ 2 SM+S1, χ 2 SM+S1) = (Φ kn
, Hˆ Φ kn
)
=1
S =0
Φ kk
= ϕ kϕ k
Ekk = (ϕ kϕ k , Hˆ ϕ kϕ k ) =
= (ϕ kϕ k , h1ϕ kϕ k ) + (ϕ kϕ k , h2ϕ kϕ k ) + (ϕ kϕ k ,V12ϕ kϕ k ) =
= 2(ϕ k , hϕ k )(ϕ k ,ϕ k ) + (ϕ kϕ k ,V12ϕ kϕ k ) = 2 h k + J kk
W oddziaływaniu
wyst puje tylko całka kulombowska.
W przypadku konfiguracji zbudowanej z jednego (tego samego) orbitala dla
obu elektronów – równowa nych elektronów – nie pojawia si efekt wymienny.
Układ dwóch elektronów – przybli enie jednoelektronowe
Jak wybra funkcje jednoelektronowe?
Jako punkt wyj cia do przybli enia jednoelektronowego mo na wybra
przybli enie nieoddziałuj cych elektronów – jako orbitale wybra rozwi zania
problemu jednoelektronowego
A
hˆϕm = ε mϕm , m = 1,2,
Wtedy przybli ona energia
Ekk = 2ε k + J kk
Mo na stara si wybra mo liwie najlepsze funkcje jednoelektronowe, takie
które optymalnie (w ramach opisu jednego elektronu jedn funkcj )
uwzgl dniaj wzajemny wpływ elektronów na siebie.
Ale jakie jest kryterium „optymalno ci”?
Odpowied daje zasada wariacyjna mechaniki kwantowej
i wynikaj ca z niej metoda Hartree’go-Focka.
B
Ekn = ε k + ε n + J kn + (−1) S K kn