1
Elektrony i dziury w
półprzewodnikach
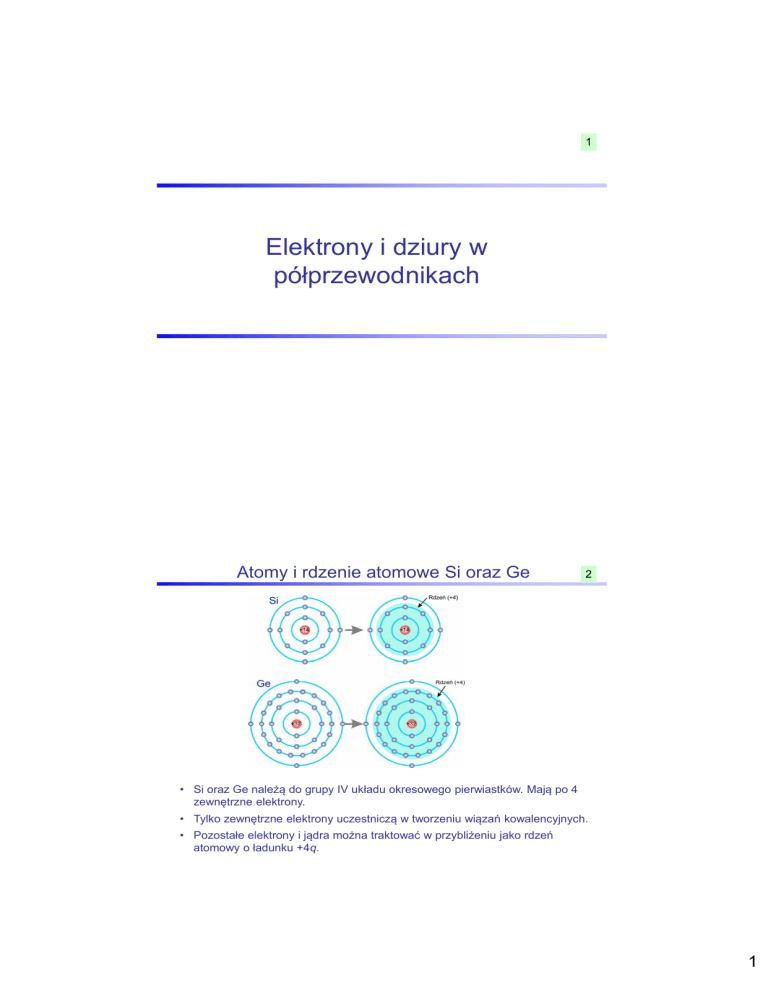
Atomy i rdzenie atomowe Si oraz Ge
2
• Si oraz Ge należą do grupy IV układu okresowego pierwiastków. Mają po 4
zewnętrzne elektrony.
• Tylko zewnętrzne elektrony uczestniczą w tworzeniu wiązań kowalencyjnych.
• Pozostałe elektrony i jądra można traktować w przybliżeniu jako rdzeń
atomowy o ładunku +4q.
1
Wiązania kowalencyjne w krysztale Si
3
Atom Si w sieci krystalicznej dzieli się swoimi 4
elektronami walencyjnymi z 4 otaczającymi go
atomami, tworząc wiązanie kowalencyjne.
Energia
Energetyczny model pasmowy półprzewodnika
4
Kryształ jako zbiór
periodycznie rozłożonych
studni potencjału.
położenie
• W półprzewodniku, w wyniku oddziaływania rdzeni atomowych, dochodzi do
utworzenia pasma przewodnictwa.
• Jest ono oddzielone przerwą energetyczną od pasma walencyjnego.
• Elektrony pasma walencyjnego i niższych nie mogą poruszać się swobodnie
po krysztale.
W. Marciniak, „Przyrządy półprzewodnikowe i układy scalone”, WNT, 1979
2
Krzem krystalizuje w strukturze diamentu
5
Si
α
Si Si
Si
Si
ostrosłup
Krzem jest czterowartościowy, więc w sieci
krystalicznej tworzy atom w środku
ostrosłupa trójkątnego regularnego ze
związanymi z nim atomami Si w
wierzchołkach
Wiązania między ostrosłupami dają sieć
z komórką regularną, powierzchniowo
centrowaną – Si, Ge, C (diament)...
S.M.Sze, Kwok K.Ng, Physics of
Semiconductor Devices, 3 ed, Wiley,
2006
GaAs krystalizuje w strukturze blendy cynkowej
6
Atom jednej grupy jest w środku
ostrosłupa trójkątnego regularnego
tworzonego przez atomy innej grupy
GaAs, GaP, InP, InAs....
3
Równanie Schrödingera dla elektronu w sieci krystalicznej
7
a – niech będzie wielkością komórki sieci kryształu o strukturze regularnej (kubicznej).
Równanie Schrödingera dla pojedynczego elektronu w sieci krystalicznej po wielu
przybliżeniach:
2 2
∇ + V (r ) Ψ (r , k ) = E (k )Ψ (r , k )
−
2m
gdzie
=
h
2π
h – stała Plancka;
r = (x,y,z)T - wektor współrzędnych położenia w przestrzeni XYZ;
k - wektor falowy;
m - masa elektronu;
V(r) – przestrzennie periodyczny rozkład energii potencjalnej pola elektrycznego sieci
krystalicznej;
E(k) – dozwolone wartości energii elektronu (wartości własne);
Ψ(r,k) – funkcja falowa elektronu.
Zależność dyspersji pomiędzy wektorem falowym, energią elektronu 8
E(k)
S.M.Sze, Kwok K.Ng, Physics of
Semiconductor Devices, 3 ed, Wiley, 2006
Si
GaAs
Energia (eV)
Energia (eV)
dno pasma przewodnictwa
schematycznie zaznaczono elektrony -
szczyt pasma walencyjnego
schematycznie zaznaczono dziury +
ka=−π
ka=0
ka=π
zredukowany wektor falowy k·a
ka=−π
ka=0
ka=π
zredukowany wektor falowy k·a
4
Masa efektywna, prędkość grupowa i pseudopęd elektronu
S.M.Sze, Kwok K.Ng, Physics of
Semiconductor Devices, 3 ed, Wiley, 2006
9
W pobliżu ekstremów pasm zależność E(k)
można aproksymować parabolą
Si
E ( k ) = E0 +
dno pasma
przewodnictwa
2k 2
2m*
gdzie masa efektywna elektronu m*
Energia (eV)
1
1 ∂ 2 E (k )
=
m* 2 ∂k 2
W przypadku ogólnym masa efektywna jest
tensorem mij*
1
1 ∂ 2 E (k )
≡ 2
*
mij ∂ki ∂k j
szczyt pasma
walencyjnego
Prędkość grupową elektronu określamy jako
vg =
ka=−π
ka=0
ka=π
zredukowany wektor falowy k·a
1 dE
dk
Pseudopęd elektronu określamy jako
p = ħk
10
Przerwa energetyczna Eg
S.M.Sze, Kwok K.Ng, Physics of
Semiconductor Devices, 3 ed, Wiley, 2006
Elektrony (ani dziury) nie mogą obsadzać
stanów energetycznych w przerwie
energetycznej (paśmie zabronionym)
Si
Ev < E < Ec
Energia (eV)
dno pasma
przewodnictwa
gdzie
Eg = Ec - Ev
szerokość przerwy energetycznej.
Zależność Eg(T) dla
Si oraz GaAs
szczyt pasma
walencyjnego
ka=−π
ka=0
ka=π
zredukowany wektor falowy k·a
5
Z okresowym ułożeniem atomów w krysztale wiąże się struktura pasmowa
11
• Elektrony, te które są, mogą się swobodnie (prawie) poruszać w paśmie przewodnictwa
• Dziury – braki elektronów, mogą się swobodnie (prawie) poruszać w paśmie
walencyjnym
Strukt_pasmowa_2
amorficzny Si – 1
Struktura energetyczna półprzewodników amorficznych
12
H
H
H
H
H
H
Schematyczna reprezentacja
amorficznego Si. Struktura ma
defekty - brakujące atomy,
„wiszące” wiązania.... Nie ma
uporządkowania dalekiego
zasięgu.
Schematyczna reprezentacja
ułożenia atomów w krysztale
Si
Dwuwymiarowa schematyczna
reprezentacja amorficznego Si
z „wiszącymi” wiązaniami
zakończonymi atomami
wodoru. Liczba atomu wodoru
- zawyżona
Półprzewodnik amorficzny:
• Brak uporządkowania dalekiego zasięgu.
• Uporządkowanie bliskiego zasięgu - na
odległość typowo 1 nm.
• Duża koncentracja defektów.
Kasap, Capper, Springer Handbook of
Electronic and Photonic Materials, 2006
S.O.Kasap, Principles of Electronic
Materials and Devices, McGraw-Hill, 2002
6
Struktura energetyczna półprzewodników amorficznych
amorficzny Si - 2
Dwuwymiarowa schematyczna
reprezentacja amorficznego Si
H z „wiszącymi” wiązaniami
zakończonymi atomami
wodoru. Liczba atomu wodoru
- zawyżona
H
H
H
H
E
Ec
H
13
stany związane z brakiem
uporządkowania dalekiego
zasięgu
stany związane z defektami
Ev
stany związane z brakiem
uporządkowania dalekiego
zasięgu
N(E)
Rozkład gęstości stanów w funkcji energii N(E)
Gęstość stanów w zakresie energii Ev < E < Ec nie jest zerowa jak
dla idealnego kryształu
M.Polowczyk, E.Klugmann, Przyrządy
Półprzewodnikowe", Wyd.PG, 2001
Półprzewodnik samoistny - monokryształ
e–
h+
14
W idealnym krysztale półprzewodnika,
bez defektów – również bez domieszek,
w temperaturze zera bezwzględnego
pasmo walencyjne powinno być pozbawione dziur,
a w paśmie przewodnictwa nie powinno być elektronów
Dla T > 0 K termiczne drgania atomów prowadzą do
zerwania niektórych wiązań i generacji par elektron-dziura
o koncentracji odpowiednio ni = pi.
Elektrony w paśmie przewodnictwa i dziury w paśmie
walencyjnym mogą przewodzić prąd elektryczny.
Thermal vibrations of atoms can break
bonds and thereby create electron-hole
pairs.
S.O.Kasap, Principles of Electronic
Materials and Devices, McGraw-Hill, 2002
T.Floyd, Electronic Devices,
Prentice-Hall, 1999
7
Temperaturowa zależność koncentracji nośników
samoistnych ni w GaAs, Si oraz Ge
ni(Eg, T)
600°C 400°C 200°C
27°C 0°C
Intensywność generacji termicznej
par elektron-dziura zwiększa się ze
wzrostem T.
1018
Koncentracja samoistna ni [cm-3]
15
2,4·1013 cm-3
1015
Zależy również wykładniczo od
szerokości przerwy energetycznej Eg.
Ge
1012
EgGe=0,7 eV
1,45·1010
109
EgSi=1,1 eV
Si
106
103
cm-3
2,1·106 cm-3
efektywne gęstości stanów
EgGaAs=1,4 eV
GaAs
1
1,5
2,5
2
3
1000/T [1/K]
S.O.Kasap, Principles of Electronic
Materials and Devices, McGraw-Hill, 2002
Eg
ni = pi = N *c N *v ⋅ exp −
2 k BT
3,5
4
Dla Si w temperaturze 300 K
ni(300K) = pi(300K) ≈ 1,45·1010 cm-3
kB – stała Boltzmanna, 1,38·10-23 J/K
Ruch dziury w paśmie walencyjnym
T.Floyd, Electronic Devices,
Prentice-Hall, 1999
16
„Oswobodzenie” elektronu –
przejście do pasma przewodnictwa
zostawia dziurę w paśmie
walencyjnym
ruch elektronu
pasma walencyjnego
odpowiadający mu
ruch dziury
Bariera energetyczna pomiędzy dziurą, a elektronami walencyjnymi sąsiednich atomów Si jest niewielka.
Termiczne drgania atomów w sieci krystalicznej wystarczają do jej pokonania i prowadzą do
przemieszczania się dziury swobodnie po krysztale w paśmie walencyjnym.
8
Półprzewodnik typu n
17
• Dodajmy atomy z grupy V układu okresowego do
krzemu, tak aby wbudowały się w jego sieć
krystaliczną.
• Atomy z grupy V – P, As, Sb - mają po 5 elektronów
w zewnętrznych powłokach.
• Tylko 4 z nich uczestniczą w tworzeniu wiązań sieci
krystalicznej krzemu.
P, As, Sb – domieszki
donorowe w krzemie
Koncentrację donorów, ich
ilość w jednostkowej
objętości, oznaczamy jako
ND
T.Floyd, Electronic Devices,
Prentice-Hall, 1999
• Piąty elektron związany jest słabo z rdzeniem atomu
domieszki.
• Termiczne drgania atomów w sieci krystalicznej
prowadzą do uwolnienia tego elektronu – może się
poruszać swobodnie po krysztale jako elektron
pasma przewodnictwa.
• Dodatnio zjonizowany atom domieszki donorowej,
np. As+, pozostaje nieruchomy.
Półprzewodnik typu p
18
• Dodajmy atomy z grupy III układu okresowego do
krzemu, tak aby wbudowały się w jego sieć
krystaliczną.
• Atomy z grupy III – B, Al, Ga - mają po 3 elektrony w
zewnętrznych powłokach.
• To o jeden elektron za mało z punktu widzenia
wiązań sieci krystalicznej krzemu.
B, Al, Ga – domieszki
akceptorowe w krzemie
Koncentrację akceptorów,
ich ilość w jednostkowej
objętości, oznaczamy jako
NA
T.Floyd, Electronic Devices,
Prentice-Hall, 1999
• Powstaje dziura w paśmie walencyjnym krzemu.
• Bariera energetyczna pomiędzy tą dziurą, a
elektronami walencyjnymi sąsiednich atomów Si jest
niewielka.
• Termiczne drgania atomów w sieci krystalicznej
wystarczają do jej pokonania i prowadzą do
przemieszczania się dziury swobodnie po krysztale
w paśmie walencyjnym.
• Ujemnie zjonizowany atom domieszki
akceptorowej, np. B-, pozostaje nieruchomy.
9
Koncentracja elektronów
koncentracja n -1
19
Koncentracja elektronów zależy od gęstości dozwolonych poziomów
energetycznych N(E) oraz prawdopodobieństwa ich obsadzenia f(E).
∞
n = N C ( E ) f ( E )dE
Ec
gdzie
NC(E)dE – gęstość stanów elektronowych (ilość na jednostkę objętości) w przedziale
energii elektronów od E do E+dE.
Gęstość stanów elektronowych NC(E) wyznacza się z zależności dyspersji E(k):
NC (E) = M C
3/ 2
2 mde
( E − Ec )1/ 2
⋅
π2
3
gdzie MC – ilość równoważnych minimów pasma przewodnictwa
mde – masa efektywna gęstości stanów pasma przewodnictwa.
Rozkład Fermiego-Diraca - prawdopodobieństwo obsadzenia stanów elektronowych f(E)
silnie zależy od temperatury
f (E) =
koncentracja n -2
1
E − EF
1 + exp
k BT
EF – poziom energii Fermiego; średnia wartość energii
elektronu w równowadze termodynamicznej
kB - stała Boltzmanna, kB = 1,38·10-23 J/K
Koncentracja elektronów
20
Koncentracje elektronów i dziur zależą od gęstości dozwolonych poziomów
energetycznych N(E) oraz prawdopodobieństwa ich obsadzenia f(E).
∞
n = N C ( E ) f ( E )dE
Ec
p = NV ( E )[1 − f ( E )]dE
Ev
−∞
10
Poziom Fermiego EF - 1
Poziom Fermiego EF
E − EF
n ≈ N C* exp − c
k BT
21
E − Ev
p ≈ NV* exp − F
k BT
E − Ev
pn ≈ N C* NV* exp − c
k BT
Dla półprzewodnika w stanie równowagi termodynamicznej iloczyn
koncentracji dziur i elektronów pn nie zależy od koncentracji donorów ND
lub akceptorów NA .
Poziom Fermiego EF - 2
Poziom Fermiego EF
22
Ec – Ev = Eg
Dla półprzewodnika w stanie równowagi termodynamicznej iloczyn
koncentracji dziur i elektronów pn nie zależy od koncentracji donorów ND
lub akceptorów NA i jest równy:
Eg
pn ≈ N C* NV* exp −
k BT
W szczególnym przypadku półprzewodnika samoistnego,
ND = NA = 0
oraz
ni = pi
Eg
= ni2
pn = N C* NV* exp −
k BT
Eg
ni = pi = N *c N *v ⋅ exp −
2 k BT
Dla półprzewodnika w stanie równowagi termodynamicznej iloczyn
koncentracji dziur i elektronów pn jest równy kwadratowi samoistnej
koncentracji elektronów ni2 .
pn = ni2
Iloczyn ten nie zależy od domieszkowania, silnie zależy od T.
11
Poziom Fermiego EF
Poziom Fermiego EF - 3
23
W stanie równowagi ładunek elektryczny elektronów i zjonizowanych
akceptorów NA- jest równoważony przez ładunek dziur i zjonizowanych
donorów ND+ :
n + NA- = p + ND+
Przy niezbyt wysokich koncentracjach, w krzemie, w temperaturze
pokojowej
NA- = NA oraz ND+ = ND
Koncentracje równowagowe elektronów n i dziur p oraz poziom energii
Fermiego EF wyznacza się z warunku równowagi elektrycznej
podstawiając:
E − EF
n ≈ N C* exp − c
k BT
Poziom Fermiego n-Si
E − Ev
p ≈ NV* exp − F
k
T
B
Poziom Fermiego EF w krzemie typu n
24
W stanie równowagi, w krzemie z przewagą donorów nad akceptorami,
ND > NA
nośniki większościowe
nośniki mniejszościowe
1
(N D − N A ) +
2
ni2
pn 0 =
nn 0
(N D − N A )2 + 4ni2
nn 0 =
E − EF
n ≈ N C* exp − c
k BT
Poziom energii Fermiego EF wyznacza się z:
Dla
N D − N A >> ni
oraz
N D >> N A
wyrażenia na koncentracje upraszczają się:
nn 0 ≈ N D
ni2
pn 0 =
ND
12
Poziom Fermiego EF w krzemie typu p
Poziom Fermiego p-Si
25
Podobnie, w stanie równowagi, w krzemie z przewagą akceptorów nad
donorami, NA > ND
1
(N A − N D ) +
2
n2
= i
p p0
nośniki większościowe
p p0 =
nośniki mniejszościowe
n p0
(N A − N D )2 + 4ni2
E − Ev
p ≈ NV* exp − F
k BT
Poziom energii Fermiego EF wyznacza się z:
Dla
N A − N D >> ni
oraz
N A >> N D
wyrażenia na koncentracje upraszczają się:
p p0 ≈ N A
Poziom Fermiego
EF
Poziom Fermiego EF - 4
n p0
ni2
=
NA
26
S.M.Sze, Kwok K.Ng, Physics of
Semiconductor Devices, 3 ed, Wiley, 2006
półprzewodnik samoistny
półprzewodnik typu n
(domieszkowany donorami)
półprzewodnik typu p
(domieszkowany akceptorami)
pasma
energetyczne
gęstości
stanów
rozkład
prawdopodobieństwa obsadzenie pasm
elektronami i dziurami
dla elektronów
13
Położenie poziomu Fermiego wewnątrz przerwy energetycznej
Si oraz GaAs w zależności od domieszkowania
Si
27
GaAs
S.M.Sze, Kwok K.Ng, Physics of
Semiconductor Devices, 3 ed, Wiley, 2006
Wpływ temperatury na koncentrację elektronów w krzemie typu n
Zakres wysokich T.
Wszystkie atomy
domieszki donorowej
zjonizowane ND+ ≈ ND.
Ale ni >> ND
n ≈ ni
28
Si
ND = 1015 cm-3
Wszystkie atomy
domieszki donorowej
zjonizowane ND+ ≈ ND.
n ≈ ND
Zakres niskich T. Nie
wszystkie atomy
domieszki donorowej
zjonizowane.
Koncentracja atomów
domieszek
zjonizowanych ND+
maleje ze zmniejszaniem
T.
S.M.Sze, Kwok K.Ng, Physics of
Semiconductor Devices, 3 ed, Wiley, 2006
14
Ruch termiczny
nośników -1
Ruch termiczny nośników ładunku w półprzewodniku
29
krzem typu n
rozkład energii
elektronów i dziur
Pseudopęd elektronu p jest związany
bezpośrednio z wektorem falowym k:
energia elektronu
p = ħk
potencjalna
przy czym
*
p = m n ·v
mn*v 2
2
kinetyczna
Średnia energia kinetyczna ruchu termicznego elektronu
gdzie
Emnth =
*
mn - masa efektywna elektronu
v – wektor prędkości elektronu
ħ = h/2π
h – stała Plancka = 6,62·10-34 J·s
Ruch termiczny
nośników -2
E = Ec +
mn*v mnth
2
2
Emnth =
3
k BT
2
Średnia wartość prędkości ruchu termicznego elektronu:
vmnth =
3k BT
mn*
(kB – stała Boltzmanna)
(Si, 300 K – vthav = 200 km/s)
Ruch termiczny nośników ładunku w półprzewodniku
30
krzem typu n
rozkład energii
elektronów i dziur
Średnia energia kinetyczna
ruchu termicznego elektronu
Emnth =
3
k BT
2
Średnia wartość prędkości
ruchu termicznego elektronu:
vmnth =
3k BT
mn*
(kB – stała Boltzmanna)
λmn = vmnthτ mn
Obliczone wartości są średnie
dla chaotycznego co do kierunku
i wartości prędkości ruchu
termicznego elektronów.
Ustalają się one w wyniku
rozpraszania E oraz v w licznych
kolizjach elektronów z
drganiami sieci krystalicznej
(fononami), atomami domieszek,
innymi elektronami, dziurami ...
Analogicznie jest dla dziur!
λmn – średnia droga
swobodna elektronu między
rozproszeniami (kolizjami)
w sieci krystalicznej
τmn – średni czas
swobodnego przelotu
elektronu między
rozproszeniami (kolizjami)
w sieci krystalicznej
τ mn =
λmn
vmnth
=
λmn
3k BT
mn*
15
Średnia droga
swobodna
Średnia droga swobodna nośników ładunku w półprzewodniku
31
L >> λmn
λmn = vmnthτ mn
W krzemie, przy T = 300 K
λmn = 7 nm - średnia droga
swobodna elektronu między
rozproszeniami (kolizjami)
w sieci krystalicznej wynosi
około 7 nm.
λmn – średnia droga
swobodna elektronu między
rozproszeniami (kolizjami)
w sieci krystalicznej
τmn – średni czas
swobodnego przelotu
elektronu między
rozproszeniami (kolizjami)
w sieci krystalicznej
τ mn =
λmn
vmnth
=
Dla modelowania przyrządów
półprzewodnikowych o długości
ścieżki przepływu elektronów L
dużo większych od λmn wygodnie
jest rozpatrywać ruch elektronów
wywołany przyłożeniem napięć na
tle uśrednionego ruchu
termicznego elektronów.
W GaAs, przy T = 300 K
λmn = 100 nm.
W GaAs, przy T = 4,2 K, w
temperaturze ciekłego helu,
λmn > 1 µm.
λmn
3k BT
mn*
L << λmn
• Dla modelowania przyrządów
półprzewodnikowych o długości
L mniejszych od λmn nie możemy
tak zrobić.
• Kolizje elektronów w sieci są
nieliczne na drodze L. Można je
pomijać w analizie.
• Taki transport elektronów
nazywamy balistycznym.
Możliwe mechanizmy transportu dziur i elektronów
32
Dyfuzja i unoszenie w polu elektrycznym
L >> λmn
Si, T = 300 K
L >> 7 nm
Dla modelowania przyrządów
półprzewodnikowych o długości
ścieżki przepływu elektronów L
dużo większych od λmn wygodnie
jest rozpatrywać ruch elektronów
wywołany przyłożeniem napięć na
tle uśrednionego ruchu
termicznego elektronów.
W krzemie, przy T = 300 K
λmn = 7 nm - średnia droga
swobodna elektronu między
rozproszeniami (kolizjami)
w sieci krystalicznej wynosi
około 7 nm.
źródło
dren
• W obecnie produkowanych przyrządach odległość dren –
źródło jest tak duża, że elektrony doznają wielokrotnego
rozpraszania. Ich energie i pędy relaksują.
• Wprowadza się pojęcie średniej prędkości unoszenia w polu E
na drodze między rozproszeniami.
• Transport nośników opisywany jest przy pomocy pojęć:
dyfuzji,
i unoszenia w polu E z uśrednioną prędkością.
mechanizmy transportu – drift-dif
16
mechanizmy transportu – ballistic - 1
Możliwe mechanizmy transportu dziur i elektronów
L << λmn
Transport balistyczny
• Dla modelowania przyrządów
półprzewodnikowych o długości
L mniejszych od λmn nie możemy
rozpatrywać ruchu elektronów
wywołanego przyłożeniem
napięć na tle uśrednionego ruchu
termicznego elektronów.
• Kolizje elektronów w sieci są
nieliczne na drodze L. Można je
pomijać w analizie.
• Taki transport elektronów
nazywamy balistycznym.
33
Si, T = 300 K
L << 7 nm
źródło
dren
• Elektrony nie doznają rozpraszania na drodze źródło - dren.
Ich energie i pędy nie relaksują.
• Ich energie całkowite nie zmieniają się.
W GaAs, przy T = 300 K
λmn = 100 nm, przy T = 4,2 K
λmn > 1 µm.
W krzemie, przy T = 300 K λmn
= 7 nm
mechanizmy transportu – ballistic - 2
• W polu E na drodze bariera-dren wzrasta pęd elektronu, a
zatem jego energia kinetyczna.
• Energia kinetyczna może być bardzo wysoka, więc czas
przelotu – bardzo krótki.
• Aby uniknąć rozpraszania odległość źródło-dren powinna być
w GaAs < 20 nm, w krzemie < 5 nm.
• Takie tranzystory mogłyby działać przy f > 1012 Hz (f > 1 THz)
Możliwe mechanizmy transportu dziur i elektronów
34
Kiedy przyrząd jest tak krótki, że można pominąć rozpraszanie elektronów - transport balistyczny
Si, T = 300 K
L << 7 nm
L << λmn
• Kolizje elektronów w sieci są
nieliczne na drodze L. Można je
pomijać w analizie.
• Taki transport elektronów
nazywamy balistycznym.
W GaAs, przy T = 300 K
λmn = 100 nm, przy T = 4,2 K
λmn > 1 µm.
W krzemie, przy T = 300 K λmn
= 7 nm
źródło
dren
Transport elektronów opisujemy zgodnie z zasadami dynamiki
Newtona, używając masy efektywnej mn*. Na elektron działa siła
F wywołana przez zewnętrzne pole elektryczne E.
F = − qE
Elektron doznaje przyspieszenia a
a=−
qE
mn*
Czyli w stałym polu elektrycznym E. prędkość elektronu vn
zmienia się od wartości vn0 jak
v n (t ) = v n 0 −
qE
t
mn*
17
32 nm CMOS - driftdiffusion
Transport z rozpraszaniem elektronów czy balistyczny?
35
Charakterystyki statyczne tranzystorów z kanałami o
długości 32 nm, CMOS - FUJITSU - 2007
FUJITSU - T.Miyashita et
al. IEDM 2007 S10P03
nMOS
pMOS
We współczesnych przyrządach krzemowych
elektrony doznają wielokrotnego rozpraszania.
Si, T = 300 K
Lch = 32 nm >> λmn = 7 nm
Transport elektronów nie jest balistyczny.
HEMT 2008 ft 600
GHz - overshoot
Transport z rozpraszaniem elektronów czy balistyczny?
36
Tranzystor HEMT (high electron mobility transistor) o rekordowo wysokiej częstotliwości
granicznej fT = 628 GHz (2008 r.)
- z kanałem z InAs
- oraz In0.52Al0.48As jako materiałem bramki o dużej szerokości przerwy energetycznej – w
roli izolatora bramki
Au – metal bramki
Au – metal drenu
pasywacja
Bramka o długości
LG = 30 - 50 nm.
źródło
In0.52Al0.48As jako
izolator bramki
kanał
In0.53Ga0.47As/InAs/In0.53Ga0.47A
s
2/5/3 nm
- na podłożu InP
Obraz przekroju z transmisyjnego
mikroskopu elektronowego
MIT - Kim, Alamo, IEEE Electron Dev. Lett, v.29, p830, 2008
18
HEMT 2008 ft 600
GHz – overshoot -2
Transport z rozpraszaniem elektronów czy balistyczny?
37
HEMT o rekordowo wysokim fT = 628 GHz (2008 r.)
- z kanałem z InAs , oraz In0.52Al0.48As jako materiałem bramki, LG = 30 – 50 nm
Au – metal bramki
Au – metal drenu
pasywacja
Bramka o długości
LG = 30 - 50 nm.
źródło
In0.52Al0.48As jako
izolator bramki
kanał
In0.53Ga0.47As/InAs/In0.53Ga0.47A
s
2/5/3 nm
- na podłożu InP
MIT - Kim, Alamo, IEEE Electron Dev. Lett,
v.29, p830, 2008
• W półprzewodnikach III-V, w temperaturze pokojowej λmn > 100 nm.
• Ale tylko dla niewielkich napięć dren – źródło.
• Ocenia się, że dla realnie pracujących przyrządów transport balistyczny
powinien dominować przy długości kanału Lg < 20 nm.
• Jesteśmy blisko!
HEMT 2008 ft 600
GHz – overshoot - 3
HEMT o rekordowo wysokim fT = 628 GHz (2008 r.)
- z kanałem z InAs , oraz In0.52Al0.48As jako materiałem bramki, LG = 30 – 50 nm
38
fmax – graniczna częstotliwość przy której tranzystor może wzmacniać moc,
to jest przy której Pwy / Pwe > 1
fT – graniczna częstotliwość przy której tranzystor może wzmacniać prąd, to
jest przy której, dla składowej zmiennej Id / Ig > 1
MIT - Kim, Alamo, IEEE Electron Dev. Lett, v.29, p830, 2008
19
HF transistors fmax-fT
Rekordowe częstotliwości fT i fmax tranzystorów oraz częstotliwości pracy układów fcircuit
39
(2015 r)
fmax – graniczna częstotliwość przy której tranzystor może wzmacniać moc,
to jest przy której, dla składowej zmiennej Pout / Pin > 1
fT – graniczna częstotliwość przy której tranzystor może wzmacniać prąd, to
jest przy której, dla składowej zmiennej Id / Ig > 1
Półprzewodnik w polu elektrycznym
40
E – energia
E – natężenie pola elektrycznego
Ψ – potencjał elektryczny
q – ładunek elementarny, q = -e ≈ 1,6·10-19 C = 1,6·10-19 A·s
E = − q⋅Ψ
dΨ 1 dE
= ⋅
E =−
dx q dx
EC
EC
EV
EV
kierunek pola elektrycznego E
kierunek pola elektrycznego E
20
pojecie ruchliwości
Ruchliwość nośników ładunku elektrycznego w półprzewodniku
41
Kiedy przyrząd jest tak długi, że nie można pominąć rozpraszania elektronów
L >> λmn
• Elektrony (dziury) doznają wielokrotnego rozpraszania. Ich
energie i pędy zmieniają się podlegając regułom statystycznym.
• Na tle tego ruchu termicznego rozważa się ich średnie
prędkości unoszenia vdrift w zewnętrznym polu elektrycznym E.
λmn = vmnthτ mn
λmn – średnia droga
swobodna elektronu między
rozproszeniami (kolizjami)
w sieci krystalicznej
τmn – średni czas
swobodnego przelotu
elektronu między
rozproszeniami (kolizjami)
w sieci krystalicznej
τ mn =
λmn
vmnth
=
λmn
3k BT
mn*
ruch i rozpraszanie elektronu (średnio)
bez zewnętrznego
pola elektrycznego
z zewnętrznym
polem elektrycznym
J.-P. Colinge, C.A. Colinge, "Physics of Semiconductor Devices", Springer 2002
pojecie ruchliwości
Ruchliwość nośników ładunku elektrycznego w półprzewodniku
42
Kiedy przyrząd jest tak długi, że nie można pominąć rozpraszania elektronów
L >> λmn
• Elektrony (dziury) doznają wielokrotnego rozpraszania. Ich
energie i pędy zmieniają się podlegając regułom statystycznym.
• Na tle tego ruchu termicznego rozważa się ich średnie
prędkości unoszenia vdrift w zewnętrznym polu elektrycznym E.
λmn = vmnthτ mn
• Dla niewielkich natężeń E średnia prędkość unoszenia
elektronów vdriftn:
v driftn = − μ nE
λmn – średnia droga
swobodna elektronu między
rozproszeniami (kolizjami)
w sieci krystalicznej
τmn – średni czas
swobodnego przelotu
elektronu między
rozproszeniami (kolizjami)
w sieci krystalicznej
τ mn =
λmn
vmnth
=
λmn
3k BT
mn*
• Dla niewielkich natężeń E średnia prędkość unoszenia dziur
vdriftp:
v driftp = μ pE
• ponieważ ruchliwość określana jest przez rozpraszanie, jej
wartość związana jest ze średnim czasem przelotu τmn i średnią
drogą swobodną λmn:
μn =
qτ mn
qλmn
=
*
mn
3k BTmn*
21
ruchliwość domieszkowanie
Ruchliwość nośników ładunku elektrycznego w półprzewodniku
43
W krzemie ruchliwości elektronów i dziur, µn oraz µp, wynikają
głównie z rozpraszania na:
• drganiach cieplnych sieci krystalicznej.
• atomach domieszkek – na donorach i akceptorach.
ruchliwość [cm2/(Vs)]
Si, Ge, GaAs
T = 300 K
koncentracja domieszek (cm-3)
J.-P. Colinge, C.A. Colinge, "Physics of Semiconductor Devices", Springer 2002
ruchliwość - T
Zależność ruchliwości od temperatury
44
W krzemie ruchliwości elektronów i dziur, µn oraz µp, wynikają
głównie z rozpraszania na:
• atomach domieszek – na donorach i akceptorach.
• drganiach cieplnych sieci krystalicznej
ruchliwość [cm2/(Vs)]
Si
S.M.Sze, Kwok K.Ng, Physics of
Semiconductor Devices, 3 ed, Wiley, 2006
temperatura (K)
22
Prąd unoszenia elektronów w polu elektrycznym
45
Wytwórzmy w próbce Si pole elektryczne o
natężeniu Ex i zwrocie jak na rys. Elektrony
są unoszone na prawo ze średnią prędkością
vnx. W czasie
Δt = Δx / vnx
przez prawą ścianę elementu ΔxΔyΔz
przepłyną wszystkie elektrony z tego
elementu. Elektronowy prąd unoszenia
możemy zapisać jako:
ΔI n = −
Gęstość prądu elektronowego Jnx
obliczamy jako:
J driftnx =
ΔI n
= − qnvnx
ΔyΔz
J driftnx = qnμ nEx
czyli
elektronowy i
dziurowy prąd
unoszenia
ΔQ
qnΔxΔyΔz
=−
= − qnvx ΔyΔz
Δt
Δt
Prąd unoszenia w polu elektrycznym
46
Gdy koncentracje elektronów w próbce półprzewodnika są stałe:
J driftnx = qnμ nEx
J driftpx = qpμ pEx
gdzie Jdriftnx i Jdriftpx są elektronową i dziurową składową gęstości prądu unoszenia Jdriftx w
kierunku x.
J driftx = qnμ nEx + qpμ pEx
Konduktywność σ (przewodność właściwa, odwrotność rezystancji
właściwej – rezystywności ρ)
σ=
1
ρ
=
J drifx
Ex
= qnμ n + qpμ p
Dla półprzewodnika typu n często
nn ≈ N D >> pn ≈
ni2
nn
23
elektronowy prąd
unoszenia
Prąd unoszenia w polu elektrycznym
47
Dla półprzewodnika typu n często
nn ≈ N D >> pn ≈
czyli
ni2
nn
J driftnx >> J driftpx
J driftx ≈ J driftnx = qnμ nEx
Konduktywność σ (przewodność właściwa, odwrotność rezystancji
właściwej – rezystywności ρ)
σ=
dziurowy prąd
unoszenia
1
ρ
≈ qnμ n
Prąd unoszenia w polu elektrycznym
48
Dla półprzewodnika typu p często
p p ≈ N A >> n p ≈
czyli
ni2
pp
J driftpx >> J driftnx
J driftx ≈ J driftpx = qpμ pEx
Konduktywność σ (przewodność właściwa, odwrotność rezystancji
właściwej – rezystywności ρ)
σ=
1
ρ
≈ qpμ p
24
rezystywność
półprzewodnika
Rezystywność półprzewodnika
49
Dla ND, NA >> ni:
Si
300 K
ρp ≈
rezystywność [Ωcm-3]
1
ρn ≈
qnn μ n
1
qp p μ p
koncentracja domieszek (cm-3)
S.M.Sze, Kwok K.Ng, Physics of
Semiconductor Devices, 3 ed, Wiley, 2006
vdrift vs. E
Prędkość unoszenia nośników w zależności od natężenia pola elektrycznego
50
Dla niewielkich natężeń
pola elektrycznego E
prędkość unoszenia
nośników [cm/s]
S.M.Sze, Kwok K.Ng, Physics of
Semiconductor Devices, 3 ed, Wiley, 2006
v driftn = − μ nE
natężenie pola elektrycznego E [V/cm]
v driftp = μ pE
Dla dużych natężeń
pola elektrycznego E, w krzemie E > 104 V/cm
vdriftn = vsatn
vdriftp = vsatp
25
Jonizacja zderzeniowa
– mechanizm przebicia lawinowego
impact ionization-1
51
Przy bardzo dużych natężeniach pola
elektrycznego E, w krzemie rzędu 106 V/cm,
mimo rozpraszania niektóre nośniki zyskują na
tyle duże energie, że dochodzi do jonizacji
zderzeniowej
współczynnik jonizacji zderzeniowej [cm--1]
- elektron z pasma przewodnictwa przekazuje
elektronowi walencyjnemu energię
wystarczającą by go wprowadzić do pasma
przewodnictwa; generowana jest dodatkowa
para elektron-dziura;
- proces ten może zachodzić lawinowo –
przebicie lawinowe.
S.M.Sze, Kwok K.Ng, Physics of
Semiconductor Devices, 3 ed, Wiley, 2006
impact ionization-2
Jonizacja zderzeniowa – mechanizm przebicia lawinowego
S.M.Sze, Kwok K.Ng, Physics of
Semiconductor Devices, 3 ed, Wiley, 2006
52
- Współczynnik jonizacji zderzeniowej mniejszy dla
większych szerokości przerwy energetycznej Eg ;
współczynnik jonizacji zderzeniowej [cm--1]
współczynnik jonizacji zderzeniowej [cm--1]
współczynnik jonizacji zderzeniowej [cm--1]
- Współczynnik jonizacji zderzeniowej maleje ze
wzrostem T.
Si
26
Dyfuzja dziur i
elektronów - 1
Prądy dyfuzji dziur i elektronów
53
Kiedy przyrząd jest tak długi, że nie można pominąć rozpraszania elektronów
L >> λmn
• Załóżmy, że w próbce wpółprzewodnika, np. Si, występuje nierównomierny rozkład koncentracji
elektronów lub dziur.
• W takiej sytuacji konsekwencją skończonej gęstości stanów funkcji energii nośników są strumienie
dyfuzji elektronów lub dziur, czyli prądy dyfuzyjne – „próbujące wyrównać koncentracje”.
• Koncentracje elektronów lub dziur, ustalają się w wielu cyklach przepływu i rozpraszania.
• Prądy dyfuzyjne płyną nawet jeżeli natężenie pola elektrycznego E jest zerowe.
Dyfuzja dziur i
elektronów - 2
Prądy dyfuzji dziur i elektronów
54
• Załóżmy, że w próbce wpółprzewodnika, np. Si, występuje nierównomierny rozkład koncentracji
elektronów lub dziur.
• W takiej sytuacji konsekwencją skończonej gęstości stanów funkcji energii nośników są strumienie
dyfuzji elektronów lub dziur, czyli prądy dyfuzyjne – „próbujące wyrównać koncentracje”.
• Koncentracje elektronów lub dziur, ustalają się w wielu cyklach przepływu i rozpraszania.
• Prądy dyfuzyjne płyną nawet jeżeli natężenie pola elektrycznego E jest zerowe.
J difnx = qDn
dn
dx
J difpx = − qD p
dp
dx
gdzie stałe dyfuzji Dn oraz Dp
określają zależności Einsteina:
Dn = μ n
k BT
q
Dp = μ p
k BT
q
27
prad przewodzenia
Gęstość prądu przewodzenia J w półprzewodniku
55
Gęstość składowej elektronowej prądu przewodzenia Jn jest sumą składowej unoszenia w
polu elektrycznym E oraz składowej dyfuzyjnej:
J nx = J driftnx + J difnx
dn
dx
J nx = qnμ nEx + qDn
Gęstość składowej dziurowej prądu przewodzenia Jp
J px = J driftpx + J difpx
J px = qpμ pEx − qD p
dp
dx
Gęstość prądu przewodzenia J w półprzewodniku:
J x = J nx + J px
Natężenie pola elektrycznego w niejednorodnie domieszkowanym półprzewodniku 56
• Załóżmy, że próbka półprzewodnika, np. Si, jest nierównomiernie domieszkowana donorami lub
akceptorami.
• Niech próbka znajduje się w stanie równowagi termodynamicznej, czyli:
2
i
pn = n
J nx = 0
0 = qnμ nEx + qDn
czyli
Ew
niejednorodnym
polprzewodniku
-1
dn
dx
Równanie to oznacza, że w stanie równowagi termodynamicznej składowe unoszenia i
dyfuzyjna są równe co do wartości, ale mają przeciwne znaki – wypadkowo znoszą się.
Przy uwzględnieniu zależności Einsteina na stałą dyfuzji Dn :
Dn = μ n
k BT
q
Natężenie pola elektrycznego Ex w niejednorodnym półprzewodniku w stanie równowagi
wynosi:
k T 1 dn( x)
k T 1 dp ( x)
Ex = −
B
q
⋅
n( x) dx
W półprzewodniku typu n, gdy n ≈ ND >> ni :
Ex = −
1 dN D ( x)
k BT
⋅
q N D ( x) dx
Ex =
B
q
⋅
p ( x) dx
W półprzewodniku typu p, gdy p ≈ NA >> ni :
Ex =
1 dN A ( x)
k BT
⋅
q N A ( x) dx
28
generacja rekombinacja - 1
Generacja i rekombinacja elektronów i dziur
57
• W półprzewodnikach zachodzą procesy generacji i rekombinacji par elektron-dziura;
• samorzutnie – pod wpływem drań termicznych sieci krystalicznej,
• lub wymuszone, np. przez oświetlenie.
Modele generacji i rekombinacji
pośredniej w Si, Ge, SiC ...
bezpośredniej w GaAs, GaN ...
Niech generacja i rekombinacja par elektron-dziura zachodzi równomiernie i niech przez półprzewodnik
nie płynie prąd.
generacja rekombinacja - 2
Generacja i rekombinacja elektronów i dziur
58
Niech generacja i rekombinacja par elektron-dziura zachodzi równomiernie i niech przez półprzewodnik
nie płynie prąd.
n − n0
∂n
= Gn − U n = G −
∂t
τ
generacja spowodowana
czynnikiem zewnętrznym
p − p0
∂p
= Gp −U p = G −
∂t
τ
zanik koncentracji
nadmiarowej w warunkach
równowagi
n0 , p0 - koncentracje równowagowe elektronów i dziur.
Gn , Gp - szybkości generacji elektronów i dziur.
Un , Up - szybkości rekombinacji elektronów i dziur.
G - szybkość generacji (lub rekombinacji jeśli ujemna) spowodowana czynnikiem zewnętrznym.
τn = τp = τ - czas życia nośników nadmiarowych.
29
generacja rekombinacja - 3
Generacja i rekombinacja elektronów i dziur - przykład
59
Próbkę krzemu typu n oświetlono równomiernie światłem o energii kwantu promieniowania większej od
Eg. W chwili t = 0 oświetlenie wyłączono. Jak zmienia się w czasie koncentracja dziur pn?
p − pn 0
∂p
=G− n
τ
∂t
G(t<0) > 0
G(t≥ 0) = 0
pn0 ≈ ni2/ND - koncentracja równowagowa dziur.
τn = τp = τ - czas życia nośników nadmiarowych.
G - szybkość generacji spowodowana oświetleniem.
p n − pn 0
pn 0
Rozwiązanie dla dwóch różnych wartości czasów
życia nośników nadmiarowych
τ = τp1 oraz τ = τp2 = 10τp1
ciaglosc ladunku
Prawo ciągłości ładunku
60
Zaniedbajmy generację i rekombinację.
Do elementu ΔxΔyΔz wpływa prąd elektronowy Inx = Jnx ΔxΔyΔz
a wypływa z niego Inx + ΔInx = (Jnx + ΔJnx)ΔxΔyΔz
Różnica ΔInx ładuje element ΔxΔyΔz:
ΔQ = −ΔI n ⋅ Δt
ΔQ = − q∂nΔxΔyΔz
− ΔI n ⋅ ∂t = −ΔJ n ⋅ ΔyΔz ⋅ ∂t
∂n 1 ∂J n
=
∂t q ∂x
Po uwzględnieniu dodatkowo szybkości generacji Gn i rekombinacji Un otrzymujemy prawo ciągłości
ładunku elektronów:
1 ∂J n
∂n
= Gn − U n +
∂t
q ∂x
Podobnie - prawo ciągłości ładunku dziur:
∂p
1 ∂J p
= Gp −U p −
∂t
q ∂x
30
podstawowe
rownania
Podstawowe równania dla analizy działania przyrządów
∂ Ψ q (n − p + N − N
=
∂x 2
εε 0
−
A
2
Równanie Poissona – na
rozkład potencjału Ψ :
Równanie ciągłości ładunku
elektronów:
Równanie ciągłości ładunku
dziur:
1 ∂J n
∂n
= Gn − U n +
∂t
q ∂x
∂p
1 ∂J p
= Gp −U p −
∂t
q ∂x
Równanie na gęstość prądu
przewodzenia elektronów:
J nx = qnμ nEx + qDn
dn
dx
Równanie na gęstość prądu
przewodzenia dziur:
J px = qpμ pEx − qD p
dp
dx
Równanie na całkowitą
gęstość prądu przewodzenia:
J x = J nx + J px
+
D
)
61
UWAGA:
Można stosować
tylko gdy długość
ścieżki przepływu
nośników ładunku
elektrycznego jest
dużo większa niż
średnia droga
swobodna nośników
pomiędzy
rozproszeniami.
L >> λmn
Ten układ równań z odpowiednimi warunkami brzegowymi i początkowymi jest rozwiązywany przez
cyfrowe symulatory przyrządów elektronicznych. Rozwiązania analityczne wymagają uproszczeń.
62
Dziękuję za uwagę!
31