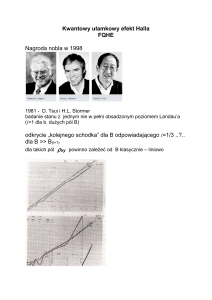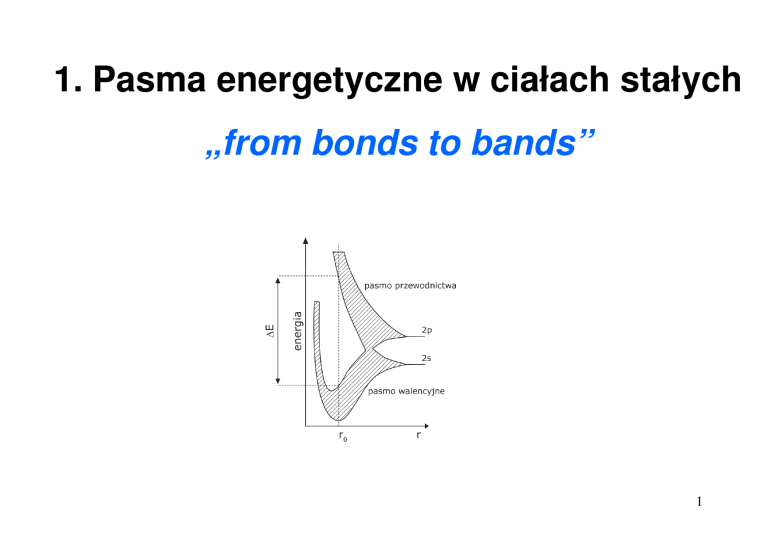
1. Pasma energetyczne w ciałach stałych
„from bonds to bands”
1
Atomy wieloelektronowe
poziomy energetyczne, maksymalna liczba elektronów
stan
główna liczba
kwantowa
orbitalna
liczba
kwantowa
magnetyczna
liczba
kwantowa
1s
1
0
0
1
1
+ , −
2
2
2
2s
2
0
0
1
1
+ , −
2
2
2
-1, 0, +1
1
1
+ , −
2
2
6
0
1
1
+ , −
2
2
2
-1, 0, +1
1
1
+ , −
2
2
6
-2,-1,0,1,2
1
1
+ , −
2
2
10
2p
3s
3p
3d
2
3
3
3
1
0
1
2
spinowa
liczba
kwantowa
maksymlana
liczba
elektronów
2
BIIICVI2
8 elektronów – zamknięta powłoka
3
Krzem i german
1s22s22p63s23p2
14 elektronów
1s22s22p63s23p63d104s24p2
32 elektrony
4
Pasma energetyczne w ciałach stałych
Poziomy energetyczne
w pojedynczym atomie
oddziaływanie z sąsiednimi atomami -
rozszczepienie poziomów w pasma
liczba poziomów w paśmie: (2l+1)*Natomów
5
Rozszczepienie poziomów energetycznych w ciele stałym cd
energia
puste
pełne
pełne
6
Wiązania kowalencyjne
(cząsteczka H2 )
7
Szerokość przerwy energetycznej zależy m.in.
od odległości między atomami w krysztale!
8
Pasmo walencyjne, przewodnictwa i przerwa energetyczna
rozszczepienie poziomow energetycznych zależy od siły oddziaływania
między elektronami z danej powłoki:
wiekszy atom
słabsze oddziaływanie
węższa przerwa energetyczna
9
III-V
Eg [eV]
GaN
GaP
GaAs
GaSb
3.4
2.25
1.52
0.81
InP
InAs
InSb
1.42
0.43
0.24
II-VI
ZnS
ZnSe
ZnTe
CdTe
HgTe
Eg [eV]
3.54
2.7
2.25
1.56
-0.01
10
Półprzewodniki mieszane – Hg1-xCdxTe
Część atomów jednego pierwiastka jest zastępowana
przez atomy innego pierwiatka z tej samej grupy układu okresowego
11
Półprzewodniki mieszane – sposób na regulację
szerokości przerwy energetycznej
AlxGa1-xAs
GaAs
Al
0.5Ga 0.5As
AlAs
12
Rodzaje struktury ciał stałych
Symetria translacyjna
R =n1 a1 + n2 a2 + n3 a3
Komórka elementarna
podstawowa cegiełka, może
zawierać więcej niż jeden atom
Komórka prosta
wyznaczona przez wektory a1, a2, a3
Np. sieć regularna przestrzennie centrowana
Sieć regularna powierzchniowo centrowana komórka elementarna i komórka prosta
(zakreskowana)
Symetria wiazania
kowalencyjnego
Struktura diamentu (dwie przesunięte
względem siebie o a/4 sieci regularne
powierzchniowo centrowane)
Struktura blendy cynkowej
(ZnS, GaAs)
Opis kwantowy elektronu w sieci periodycznej
Elektron w pustej przestrzeni
− h2 2
∆ Ψ = EΨ
2m
Ψ k = Ae
rr
ik r
2π
λ
h hk
p= =
= hk
λ 2π
k≡
relacja de Broghlie’a
Elektron w potencjale periodycznym
r r
r
− h2 2
∆ Ψ + UΨ = EΨ
U( r ) = U( R + r )
2m
rr
r
r
ik r
uk(r) = uk(r+R)
Ψ( r ) = Ψ( R + r)
⇒ Ψ k = u k (r)e
Funkcja Blocha – funkcja falowa
k - wektor quasi-falowy
opisująca elektron w polu periodycznym, odpowiada quasi-pędowi elektronu
wektor k określa stan elektronu
p=ħk
W idealnej sieci bez zewnętrznych zaburzeń elektron nie zmienia swojego stanu
k=const
Zależność E(k) to ekwiwalent zależności E(p)!
E(k) dla elektronu w periodycznej
sieci
Periodyczność w przestrzeni:
x=x+a: Ψ= uk(x)eikx = uk(x+a)eik(x+a)
periodyczność quasi-pędu:
k=k+2π
π/a
Ψ= uk(x)eikx = uk+2π/a(x)ei(k+2π/a)x
E(k) dla swobodnego
elektronu
E(k)=E(k+2π
π/a)
Energia elektronu w periodycznej sieci
jest periodyczną funkcją pędu (czyli k)
Ograniczony zakres quasi-pędu
(-π/a, π/a)
wystarczy żeby w pełni opisać elektron
I strefa Brillouine’a
-π/a
0
π/a
-π/a
π/a
k
Struktura pasmowa półprzewodników
swobodny elektron w próżni:
elektron w sieci
periodycznej
p2
E (p ) =
2m
E(k)
Pasmo
przew
p2
h 2k 2
E(p) =
=
2m * 2m *
m* - masa efektywna elektronu w pasmie
Prędkość elektronu
r
r hk
v=
m*
Dynamika elektronu:
r
r
r
r
dp
dk
dv
= h
= m *
= F zew
dt
dt
dt
k
Pasmo
walenc
Przerwa prosta i przerwa skośna
przerwa prosta
GaAs, CdS, CdSe, ZnS,
InSb, HgTe, GaN
przerwa skośna
Si, Ge, GaP, AlAs
19
Elektrony i dziury
generacja termiczna pary elektron-dziura
EF
+
CB
CB
VB
VB
energia elektronów
CB
VB
energia dziur
Struktura pasmowa - przykłady
Si
GaAs
K
Przerwa skośna
k
wave vector k
k
Przerwa prosta
Struktura pasmowa - przykłady
p. przew
p. walenc.
22