Wykład VII pasma energetyczne

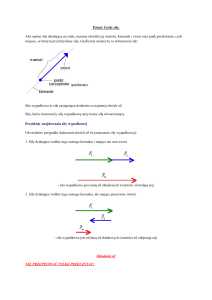
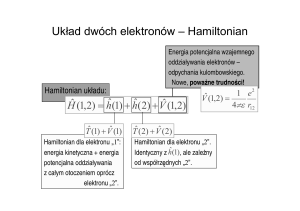
Wykład VIII. Pasma energetyczne.
Aby otrzymać strukturę elektronową kryształu możemy posłużyć się dwoma modelami: modelem
elektronów silnie zlokalizowanych ( model ciasnego wiązania ) i modelem elektronów prawie swobodnych.
W modelu ciasnego wiązania w tzw. zerowym przybliżeniu zakładamy, że mamy elektrony
znajdujące się w stanach atomowych, określonych przez potencjał pojedynczego jonu ( atomu) zaś efekt
kryształu pojawia się jako zaburzenie pochodzące od pozostałych jonów ( atomów) sieci krystalicznej.
Elektron jest więc przede wszystkim elektronem związanym z konkretnym atomem, a jego ruch jest
dodatkowo zaburzony przez pozostałe atomy sieci.
W modelu prawie swobodnych elektronów w zerowym przybliżeniu zakłada się, że elektrony w
krysztale są elektronami swobodnymi, nie związanymi z żadnym konkretnym atomem , zaś periodyczny
potencjał jonów ( wszystkich) może być traktowany jako zaburzenie. Elektron jest więc przede wszystkim
elektronem swobodnym , którego ruch jest zaburzony przez atomy sieci.
Jeśli rozważa się bardziej zaawansowane wersje obu modeli i przeprowadza w ich ramach obliczenia
to otrzymuje się lepsze wyniki gdy używa się modelu ciasnego wiązania do opisu elektronów w rdzeniach
atomowych atomów sieci. Jednak, jeśli interesujemy się elektronami walencyjnymi, odpowiedzialnymi za
wiązania krystaliczne i własności elektryczne kryształów to nieco lepsze wyniki otrzymuje się stosując model
słabego wiązania. Ogólnie trudno jest jednak przedstawić jednoznacznie kiedy jaki model będzie poprawniej
opisywał rzeczywistość. Fakt, że otrzymuje się taki sam lub prawie taki sam wynik stosując różne modele, i że w
obu przypadkach całkowicie poprawnie opisujemy rzeczywistość jest jednym z bardziej interesujących
przykładów zastosowania metod przybliżonych do opisu zjawisk fizycznych . W naszym przypadku ta pozorna
sprzeczność ma stosunkowo proste wyjaśnienie. Kryształ stanowi dla elektronów walencyjnych środowisko ,
które jest czymś pośrednim pomiędzy atomem a próżnią (ze względu na osłabienie oddziaływania atomu
macierzystego przez pozostałe atomy sieci) . Nie znając ścisłych rozwiązań musimy posługiwać się metodami
przybliżonymi, biorąc za punkt wyjścia znane nam układy ( atom lub jego brak). W gruncie rzeczy jest
obojętne czy do wyniku, którym jest struktura pasmowa dochodzimy od strony silnie zlokalizowanych
elektronów, zmniejszając potencjał atomu macierzystego na korzyść pozostałych atomów, czy od strony
swobodnych elektronów wprowadzając i zwiększając stopniowo potencjał sieci. W obu przypadkach wynik
powinien być w przybliżeniu taki sam. W trakcie tego wykładu zostanie przedstawiony model prawie
swobodnych elektronów.
Wprowadźmy potencjał krystaliczny , który jest dany przez funkcję V (r ) , periodyczną z okresem
sieci , tzn. spełniającą warunek V (r  R )  V (r ) , gdzie R jest dowolnym wektorem translacji. Energię
elektronu otrzymujemy rozwiązując następujące, niezależne od czasu równanie Schrodingera:
{
  2 2
 V (r )} k (r )  E (k ) k (r) ,
2m
(VIII-1)
W przypadku tego równania skorzystaliśmy z wyniku otrzymanego już dla elektronów swobodnych a
mianowicie z faktu, że energia elektronu jest funkcją wektora falowego. Jeśli potencjał krystaliczny nie jest zbyt
silny energia elektronu w krysztale również powinna zależeć od wektora falowego.
1
Tak jak to się na ogół zdarza i w tym przypadku nie potrafimy znaleźć ścisłych rozwiązań równania
(VIII-1). Istnieje co najmniej kilkanaście przybliżonych metod rozwiązywania równania (VIII-1). We
wszystkich przypadkach podstawowym zagadnieniem jest właściwy wybór ogólnej postaci funkcji falowej,
będącej jego rozwiązaniem.
Wydaje się oczywiste ,że ponieważ potencjał kryształu jest niezmienniczy względem translacji
sieci prostej, tę samą cechą powinna się charakteryzować każda inna wielkość fizyczna, w szczególności
gęstość elektronów, lub inaczej gęstość prawdopodobieństwa znalezienia elektronu wewnątrz kryształu,
dana przez
 k* (r)   k (r) . Powyższe stwierdzenie jest jednym z możliwych sformułowań tzw.
twierdzenia Blocha.
Inne sformułowanie tego twierdzenia mówi, że rozwiązania równania Schrődingera z
potencjałem periodycznym mają postać fal płaskich modulowanych przez funkcje periodyczne z
okresem sieci krystalicznej. Zgodnie z tym przyjmuje się następującą postać rozwiązań równania (VIII-1):
 k (r)  h(r)  exp[ i(kR)]
(VIII-2)
gdzie h(r ) jest funkcją periodyczną z okresem sieci prostej, czyli spełniającą warunek niezmienniczości
względem translacji sieci; R: h(r )  h(r  R ) . Funkcja (VIII-2) nazywana jest często funkcja Blocha.
Przykład funkcji Blocha znajduje się na rysunku VIII-1.
Rys.VIII-1 Konstrukcja funkcji Blocha.
Odległość jest w jednostkach stałych sieci
●
●
●
●
●
położenia atomów
Funkcja periodyczna h(r )
Obwiednia exp(kR)
Funkcja Blocha h(r )  exp( kR)
2
Łatwo zauważyć, że funkcja taka będzie również niezmiennicza ze względu na przekształcenia translacji w sieci
odwrotnej ( przesunięcie o wektor G )
 k G (r)  h(r )  exp[ i(k  G )R]  h(r )  exp[ ikR]  exp[ iGR ] 
h(r )  exp[ ikR]   k (r )
Skorzystano tu z faktu, że
(VIII-3)
GR  n2 , gdzie n jest dowolną liczbą całkowitą. Jeśli wektor r zostanie
przedstawiony przy pomocy sumy r  R  ρ , gdzie ρ jest położeniem wewnątrz komórki elementarnej
(patrz Rys VIII-2) to funkcję Blocha (VIII-2) daje się przedstawić następująco:
 k (r)  h(ρ)  exp[ ikρ]  exp[ ikρ]  exp[ ikR]  uk (r)  exp[ ikr]
gdzie funkcja,
(VIII-4)
uk (r)  uk (ρ)  h(ρ)  exp[ ikρ] , ponieważ zależy tylko od ρ , jest z definicji
niezmiennicza ze względu na operację translacji. Wzór (VIII-4) jest najczęstszym przedstawieniem funkcji
Blocha.
Rysunek (VIII-2)
Przedstawienie
położenia sieci
krystalicznej,
kwadratami
zaznaczono
poszczególne
komórki
elementarne
ρ
r
R
Bardzo pouczające jest rozpoczęcie analizy elektronowej struktury pasmowej od granicznego przypadku gdy
potencjał krystaliczny jest równy lub bliski zeru. Dla zerowego potencjału sieci zależność energii elektronów
swobodnych od pędu (lub od wektora falowego) dana jest przez zależność
2k 2
,
E (k ) 
2m
(VIII-5)
Dołączenie bardzo małego periodycznego potencjału sieci, nie powinno w istotny sposób zmienić wartości
energii, zmienia jednak w sposób jakościowy typ rozwiązań. Przede wszystkim pojawienie się potencjału
niezmienniczego ze względu na translację sieci prostej powoduje konieczność niezmienniczości rozwiązań
równania Schrődingera , ze względu na translacje sieci odwrotnej.
Rozważmy przykład jednowymiarowej sieci o stałej a . Potencjał krystaliczny V (x ) musi spełniać
warunek V ( x)  V ( x  a ) . Stała sieci odwrotnej jest równa g 
2
. Nawet w granicy V ( x )  0
a
wszystkie wielkości fizyczne zależne od wektora falowego muszą spełniać warunek
Dotyczy to również energii. Tak więc E (k )  E (k  g ) ( patrz rys. VIII-3).
3
 (k )   (k  g ) .
Rys. VII-3. Zależność
energii od wektora
falowego dla przypadku
V(r)  0. Wektor falowy
wyrażony jest w
jednostkach g 
2
a
Równanie Schrődingera dla naszego jednowymiarowego kryształu będzie maiło postać:
[
 2 d 2
 V ( x)] k ( x)  E (k )   k ( x)
2m dx 2
Łatwo zauważyć, że każda funkcja w postaci
(VIII-6)
 k  exp[ i(k  ng ) x] , gdzie n jest dowolną liczbą całkowitą
jest rozwiązaniem tego równania. Odpowiadająca jej wartość własna energii jest dana przez wzór:
E (k  ng ) 
2
(k  ng ) 2
2m
(VIII-7)
Odpowiedni wykres przedstawiający zależność energii od wektora falowego znajduje się na rysunku (VIII-3).
Na rysunku tym przedstawiono wartości własne energii dla n  1,
i
n  2 . Łatwo zauważyć, że
funkcja typu (VIII-7) reprezentuje wartości własne równania (VIII-6) dla V ( r )  0 dla dowolnych n i g. Jest
to oczywiste bowiem stały potencjał V=0 jest niezmienniczy względem dowolnej transformacji.
Powróćmy do krzywych dyspersji ( czyli zależności energii od wektora falowego, E(k)). Możemy rozważać
energię elektronu w układzie strefy rozwiniętej co odpowiada ciągłej linii na rysunku VIII-3. Tę samą
informację o energii uzyskamy gdy analizujemy dyspersję w układzie strefy zredukowanej. Odpowiada to
analizie krzywych dyspersji znajdujących w pierwszej strefie Brillouina. Widzimy , że w pierwszej strefie E(k)
nie jest określone jednoznacznie , jednej wartości wektora falowego odpowiadają dwie wartości energii.
Pojawiły się pasma energetyczne. Zależność dyspersyjna w najniższym paśmie jest dana przez funkcję
4
g
g
2 2
k , gdzie wektor falowy spełnia warunek   k  . Energia elektronów w wyższych
2
2
2m
E0 (k ) 
pasma dana jest przez
E n (k ) 
2
(k  ng ) 2 dla wektora k spełniającego warunek
2m
g
g
k .
2
2
Powyższe rozważania dotyczyły szczególnego przypadku tzw. pustej sieci i miały na celu pokazanie
jak tworzą się pasma energetyczne. Obecnie zajmiemy się przypadkiem bardziej realnym, gdzie potencjał
krystaliczny jest różny od zera.
Pozostańmy nadal przy jednowymiarowym krysztale. Jeśli potencjał V (x ) jest periodyczny z
okresem sieci prostej to w jego rozwinięciu w szereg Fouriera występować będą tylko fale o wektorach
falowych G równych wielokrotności stałej sieci odwrotnej G   ng
V ( x)  U G  e iGx
(VIII-8)
G
gdzie
U G są współczynnikami rozwinięcia. W najprostszej postaci wystarczy wziąć tylko jeden wektor
Gg
2
. Potencjał będzie miał wówczas postać kosinusoidy
a
V ( x)  2U g cos( gx)  U g {e igx  e igx }
(VIII-9)
Widać ,że część rzeczywista ma postać kosinusoidy o okresie stałej sieci prostej . W dalszym ciągu korzystać
będziemy z potencjału wyrażonego przez funkcję zespoloną
V ( x)  U g [e igx  e igx ] Równanie
Schrődingera będzie miało postać
(
 2 d 2
 U g [e igx  e igx ] k ( x)  E (k )   k ( x)
2m dx 2
(VIII-10)
Funkcja Blocha będąca rozwiązaniem powyższego równania dana jest przez relację
Periodyczna funkcja
 k ( x)  u k ( x)e ikx .
u k (x) daje się rozwinąć w szereg Fouriera. Co więcej, jeśli potencjał krystaliczny jest
dany przez (VIII-9) to przy rozwinięciu funkcji
u możemy uwzględnić tylko dwie składowe odpowiadające
wektorom sieci odwrotnej 0 i g. Ostatecznie więc mamy następującą postać funkcji Blocha :
 k ( x)  u k ( x)e ikx  C (k )e ikx  C (k  g )e ikx e igx
(VIII-11)
Podstawiamy funkcję (VIII-11) do równania (VIII-10) i wykonujemy różniczkowanie ;
2 2
2
k C (k )e ikx 
(k  g ) 2 C (k  g )e ikx e igx  U g [e igx  e igx ]{C (k )e ikx  C (k  g )e ikx e igx } 
2m
2m
E (k ){C (k )e ikx  C (k  g )e ikx e igx }
(VIII-12)
5
Aby obliczyć wartości własne energii mnożymy lewostronnie powyższe równanie przez e
 ikx
oraz przez

e  ikx e igx i wykonujemy całkowanie po x . Korzystając z następującej równości  e i ( k  k ') x dx   (k  k ' )

trzymuje się następujący układ równań:
2 2
k  E (k )}C (k )  U g C (k  g )  0
2m
2
U g C (k )  {
(k  g ) 2  E (k )}C (k  g )  0
2m
{
(VIII-13)
Układ ten ma nietrywialne rozwiązania jeśli znika jego wyznacznik. Ostatni warunek pozwala na obliczenie
wartości własnych energii:
{
2 2
2
k  E (k )}{ (k  g ) 2  E (k )}  U g2  0
2m
2m
implikuje
2 2
2 2
2
{
[k  (k  g ) 2 ]}2  4U g2
[k  (k  g ) ]
2m
E ( k )   2m

2
2
(VIII-14)
Otrzymujemy dwa rozwiązania + i - . Wykresy zależności energii od wektora falowego w obu przypadkach
przedstawione są na rysunku VIII-4.
Rys (VII-4) Struktura
pasmowa. Wektor falowy k
przedstawiony jest w
jednostkach g
Eg= 2Ug
Łatwo zauważyć ,że gdy k zbliża się do
g
g
energia przyjmuje odpowiednio wartości E ( )   U g i
2
2
6
g
E ( )   U g . Pojawia się więc przerwa energetyczna, lub inaczej mówiąc pasmo energii wzbronionej o
2
szerokości 2U g .
W rzeczywistych kryształach potencjał krystaliczny nie może być przybliżony przez pojedynczą
sinusoidę, nadal jednak możemy rozwinąć go w szereg Fouriera:
V (r)  U G e iGr
(VIII-15)
G
i użyć funkcji Blocha w postaci analogicznego rozwinięcia :
 k (r)   C (k  G )e i (k G )r
(VIII-16)
G
W rezultacie aby otrzymać wartości własne energii musimy diagonalizować układ równań , który ma wymiar
równy ilości wziętych pod uwagę w rozwinięciu (VIII-15) i (VIII-16) wektorów sieci odwrotnej. Kształt pasm
energetycznych będzie bardziej skomplikowany niż poprzednio. Wyniki obliczeń struktury pasmowej dla
kryształów krzemu i germanu przedstawione są na rysunku VIII-5. Przedstawiono tu najniższe pasma
energetyczne.
Rys.VII-5. Struktura pasmowa
Si i Ge. Na rysunku mamy
pasma o najniższej energii.
Należy zwrócić uwagę, że
dodatnia i ujemna oś odciętych
reprezentują różne kierunki
krystalograficzne Każda
krzywa odpowiada pasmu
energetycznemu.
Oba półprzewodniki są
półprzewodnikami o przerwie
skośnej, tzn. minimum pasma
przewodnictwa znajduje się w
innym punkcie pierwszej strefy
Brillouina niż maksimum
pasma walencyjnego.
Pomimo znacznych uproszczeń wiele spośród własności ciała stałego można wytłumaczyć posługując
się modelową strukturą przedstawioną na rysunku VIII-4. Mamy tu do czynienia z dwoma pasmami
7
energetycznymi. To o niższej energii zwane jest pasmem walencyjnym , to o wyższej energii pasmem
przewodnictwa. Istnienie pomiędzy nimi obszaru energii wzbronionej ( przerwy energetycznej) decyduje w
zasadniczy sposób o wielu właściwościach, w szczególności o przewodnictwie materiału.
Elektrony jako fermiony zajmują kolejno stany energetyczne, od stanu o najniższej energii do stanu o
energii Fermiego. Jeśli elektronów walencyjnych jest tyle samo ile jest stanów w paśmie walencyjnym ,
wówczas pasmo walencyjne zostaje całkowicie zapełnione a pasmo przewodnictwa jest puste. Co stanie się,
jeśli do takiego materiału przyłożymy zewnętrzne napięcie. Rozpatrzmy elektrony z pasma walencyjnego.
Dodatkowy ruch tych elektronów w kierunku pola powodowałby wzrost ich prędkości , a co za tym idzie wzrost
energii. Nie jest to jednak możliwe bowiem ponad pasmem walencyjnym brak jest wolnych stanów
energetycznych. Z kolei pasmo przewodnictwa jest całkowicie puste. W rezultacie przyłożone pole nie wywoła
ruchu elektronów. Materiał taki nie będzie przewodził prądu. Tak dzieje się w bardzo niskich temperaturach. W
wyższych temperaturach elektrony z pasma walencyjnego mogą być wzbudzane do pasma przewodnictwa gdzie
zachowywać się będą jak elektrony swobodne i będą mogły przyczyniać się do przewodnictwa.
Zależnie od wartości przerwy energetycznej mamy do czynienia z izolatorem lub półprzewodnikiem.
Jeśli E g  k B T , (w temperaturze pokojowej) , wówczas nawet w wysokich temperaturach wzbudzana będzie
znikoma ilość elektronów i materiał będzie izolatorem. Jeśli E g  () k B T wówczas mamy do czynienia z
półprzewodnikiem. W praktyce własności półprzewodnikowe mają materiały o przerwie energetycznej
mniejszej niż 3 eV. Cechą charakterystyczną półprzewodników jest to ,że ich opór elektryczny maleje
exponencjalnie z temperaturą .
Przewodnictwo typu metalicznego pojawia się gdy pasmo walencyjne jest lub pasmo przewodnictwa
jest częściowo zapełnione przez elektrony. Sytuacja obrazowana jest na rysunku VIII-6.
Rys VIII-6 Przykłady struktur pasmowej. Stany obsadzone są zacieniowane. a) izolator ( półprzewodnik), b)
metal powstały w wyniku nakładania się pasm, c) metal.
8
9