Cechy siły.

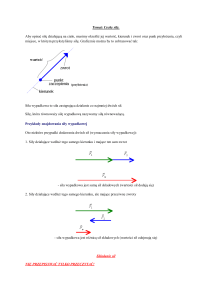
Temat: Cechy siły.
Aby opisać siłę działającą na ciało, musimy określić jej wartość, kierunek i zwrot oraz punk przyłożenia, czyli
miejsce, w którym przyłożyliśmy siłę. Graficznie można by to zobrazować tak:
Siła wypadkowa to siła zastępująca działanie co najmniej dwóch sił.
Siłę, która równoważy siłę wypadkową nazywamy siłą równoważącą.
Przykłady znajdowania siły wypadkowej
Oto niektóre przypadki dodawania dwóch sił (wyznaczania siły wypadkowej):
1. Siły działające wzdłuż tego samego kierunku i mające ten sam zwrot
- siła wypadkowa jest sumą sił składowych (wartości sił dodają się)
2. Siły działające wzdłuż tego samego kierunku, ale mające przeciwne zwroty
- siła wypadkowa jest różnicą sił składowych (wartości sił odejmują się)
Składanie sił
NIE PRZEPISYWAĆ TYLKO PRZECZYTAĆ!
W celu graficznego dodania wektorów (czyli wektorów narysowanych jako strzałki), powinniśmy zastosować
jedną z dwóch metod (można wybrać tę, która wygodniejsza w danej sytuacji):
reguła równoległoboku
Załóżmy, że początkowo mamy dwa różne wektory
- niebieski i czerwony:
Za chwilę dodamy je graficznie omawiając kolejne etapy postępowania:
Etap 1: wektory zaczepiamy we wspólnym początku (kierunek, zwrot i długość obu wektorów nie mogą ulec
zmianie). Trzeba przenieść (zachowując jego kierunek i zwrot) jeden z wektorów do początku drugiego
Etap 2: przez koniec pierwszego wektora prowadzimy prostą równoległą do drugiego wektora, a następnie przez
koniec drugiego wektora prowadzimy równoległą do pierwszego wektora.
Etap 3 (kończący dzieło): wspólny początek wektorów (początek wektora-sumy) łączymy z punktem przecięcia
prostych z utworzonych na etapie poprzednim (będzie to koniec wektora-sumy)
reguła trójkąta
Załóżmy znowu, że, jak poprzednio, początkowo mamy dwa wektory:
Aby dodać je metodą trójkąta posłużymy się następującą metodą:
Etap 1: początek jednego wektora zaczepiamy w końcu drugiego wektora. Musimy po prostu przenieść jeden
wektor zachowując jego kierunek, zwrot i długość.
Etap 2: początek pierwszego wektora (będzie to początek wektora-sumy) łączymy z końcem drugiego wektora
(będzie to koniec wektora-sumy).
Gotowe! – wektor zielony jest sumą wektorów – niebieskiego i czerwonego