Wykład 23 Baza i wymiar przestrzeni. Liniowa niezależność

Wykład 23
Baza i wymiar przestrzeni. Liniowa niezależność wektorów.
Definicja 23.1
Wektory a1, a2, …, ak  Rn nazywamy liniowo niezależnymi, jeśli ich kombinacja liniowa
jest równa wektorowi zerowemu wtedy i tylko wtedy, gdy wszystkie współczynniki tej
kombinacji są równe zeru, tzn.
l1a1 + l2a2 + … + lkak = 0  l1 = l2 = … = lk = 0
Jeśli choć jeden z tych współczynników jest różny od zera, mówimy, że wektory a1, a2, …, ak
są liniowo zależne.
Twierdzenie 23.1
Układ wektorów a1, a2, …, ak jest liniowo zależny, jeśli jeden z nich jest kombinacją liniową
pozostałych.
W takim wypadku każdy z wektorów a1, a2, …, ak jest kombinacją liniową pozostałych.
Twierdzenie 23.2
W przestrzeni Rn układ wektorów liniowo niezależnych może liczyć co najwyżej n wektorów.
Każdy układ zawierający więcej niż n wektorów jest liniowo zależny.
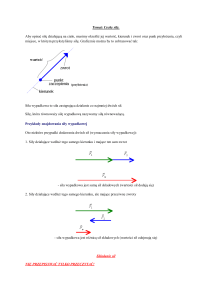
Przykład 23.1
Zbadać liniową zależność wektorów
 2
1
 3
1. a    , b    , c   
0 
5
 4
3
1
9




2. a   2  , b  1 , c   7 
 4 
5
23
3
1
2




3. a   2  , b  1 , c  2
 4 
5
1 
Rozwiązanie
ad 1
Wektory te są zależne, gdyż należą do przestrzeni R2, zatem układ wektorów niezależnych w
tej przestrzeni może liczyć co najwyżej dwa wektory.
ad 2
Zależność i niezależność układu wektorów sprawdzamy badając równanie l1a + l2b + l3c = 0.
 3
1
 9  0 
l1 2  l2 1  l3  7   0
4
5
23 0
Wykonując mnożenie i porównując współrzędne wektorów po lewej i prawej stronie
równości otrzymujemy układ równań:
 3l1  l2  9l3  0

 2l1  l2  7l3  0
4l  5l  23l  0
2
3
 1
Z pierwszego równania mamy l2 = -3 l1 - 9 l3.
 l2  3l1  9l3

Podstawiamy l2 do równania drugiego i trzeciego   l1  2l3  0
 11l  22l  0
1
3

Widzimy, że równanie trzecie jest równaniem drugim pomnożonym przez 11, zatem nie
wnosi nic do układu równań i można je pominąć. Ostatecznie otrzymujemy nieskończenie
wiele rozwiązań:
l1 = -2l3 oraz l2 = -3l3
Podstawiając np. l3 = 1 otrzymujemy -2a - 3b + c = 0
3 1  9  0
Sprawdzenie:  22  31   7   0
       
4 5 23 0
Zatem badane wektory są liniowo zależne.
Ponieważ z równości -2a - 3b + c = 0 wynika:
3
1
2
1
c = 2a + 3b, a   b  c , b   a  c
2
2
3
3
Zatem każdy z tych wektorów jest kombinacją liniową pozostałych.
ad 3
Postępując podobnie jak poprzednio otrzymujemy układ równań;
3l1  l2  2l3  0

2l1  l2  2l3  0
 4l  5l  l  0
2
3
 1
Układ ten ma jedno rozwiązanie: l1 = l2 = l3 = 0. Zatem jest to układ wektorów niezależnych.
Definicja 23.2
Bazą przestrzeni wektorowej nazywamy zbiór B wektorów tej przestrzeni taki, że:
- każdy wektor przestrzeni jest kombinacją liniową wektorów należących do B,
- wektory należące do B są liniowo niezależne.
Przykład 23.2
 2
1
Bazą przestrzeni R2 są wektory a   , b    .
 3
1
1
0
Inną bazę stanowią wersory i   , j    .
0 
1
1
0


Wektory a  3 , b  1 R3 nie stanowią bazy tej przestrzeni. Są wprawdzie liniowo
 
 
0
0
niezależne, ale generują wszystkich wektorów przestrzeni R3. Poza tym baza przestrzeni R3
musi zawierać trzy wektory.
Widzimy więc, że przestrzeń wektorowa może mieć różne bazy. Jednak wszystkie bazy tej
samej przestrzeni składają się z jednakowej liczby wektorów.
Definicja 23.3
Liczbę wektorów w bazie przestrzeni liniowej nazywamy wymiarem tej przestrzeni.
Przestrzeń R2 ma wymiar 2, R3 ma wymiar 3.