Fizyczna interpretacja rotacji

Trochę matematyki
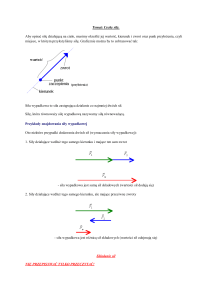
Przepływ cieczy nieściśliwej – zamrozimy ciecz w całej objętości z
wyjątkiem wąskiego kanalika o stałym przekroju – kontur . Ciecz w
kanaliku jest nieruchoma lub przepływa wzdłuż konturu .

Cyrkulacja (krążenie) wektora
wzdłuż konturu
 
Cv  v  l   vl  dl

Dla dowolnego wektora
 
Ca   a  dl


v
Cyrkulacja właściwa – stosunek cyrkulacji C do powierzchni A
„obmywanej” przez cyrkulację. Wielkość
Ca
lim
A 0 A
zachowuje się jak rzut pewnego wektora na kierunek normalnej do
płaszczyzny konturu, wzdłuż którego następuje cyrkulacja. Wektor

ten nosi nazwę rotacji wektora a

Ca
1  
rota n  lim
 lim  adl
A 0 A
A 0 A

W prostokątnym układzie współrzędnych

i
   
rota    a 
x
ax

j

y
ay

k

z
az
Twierdzenie Stokesa
  
 
 a  dl     a  dA

Cyrkulacja wektora

rot a

a
A
wzdłuż konturu  równa się strumieniowi wektora
przez dowolną powierzchnię A ograniczoną tym konturem.
Fizyczna interpretacja rotacji
W polu wektorowym o nieznikającej rotacji występują wiry – jeśli jest
to pole prędkości, to muszą wystąpić zamknięte linie (wiry), które
mogą być nałożone na jednokierunkowy przepływ.
Zmienny strumień magnetyczny generuje siłę elektromotoryczną.
Siła elektromotoryczna = praca wykonana nad jednostkowym
ładunkiem, który przemieszcza się wzdłuż obwodu
 
 
 
W   F  dl  qE  dl  q  E  dl

 
 B   B  dA
A

d B
 
dt

 
W
    E  dl
q 

 
d  
dB 
 E  dl   dt A B  dA  A dt  dA

 
d  
dB 
 E  dl   dt A B  dA  A dt  dA
Pole elektrostatyczne jest polem zachowawczym. Praca po krzywej
zamkniętej
 
 qE  dl  0

 
 E  dl  0

Otrzymany wynik jest sprzeczny z tym stwierdzeniem



d  
dB 
 EB  dl   dt A B  dA  A dt  dA
to nie jest pole statyczne



dB 
 EB  dl  A dt  dA



 
 EB  dl     EB  dA

A




 
dB 
 EB  dl  A   EB  dA  A dt  dA

 
B
  EB  
t
 

E  EB  Es
  
 
 a  dl     a  dA

A
pochodna cząstkowa, bo w
 
ogólności B  B x, y, z , t 

   

 
 
B
  E    E B  Es    E B    Es  

t


wirowe pole elektryczne
0
Zmienne pole magnetyczne wytwarza wirowe pole elektryczne.
Umieśćmy w tym polu obwód kołowy.
dB
0
dt
Strumień B rośnie – zgodnie z
regułą Lenza prąd płynący w
obwodzie kołowym
przeciwstawia się tej zmianie –
pole wytworzone przez ten prąd
ma kierunek przeciwny do zmian
pola zewnętrznego - jest
skierowane w dół
dB
0
dt
Strumień B maleje – zgodnie z
regułą Lenza prąd płynący w
obwodzie kołowym przeciwstawia się
tej zmianie – pole wytworzone przez
ten prąd ma kierunek przeciwny do
zmian pola zewnętrznego - jest
skierowane w górę
Prawo Ampere’a raz jeszcze
 
 B  dl  0 I
  
 
 a  dl     a  dA
 
I   j  dA


A
  
 
   B  dA  0  j  dA
A
A
 

  B  0 j
A
Obliczymy dywergencję:


  
 
    B  0  j
= 0 zawsze!!!
pole jest albo źródłowe albo wirowe
?
Prawo Ohma


  
 
    B  0  j


j  E
Obliczmy dywergencję tego równania
 

E 
 
 
  j    E
 
 j  0
 0 r

prawo Gaussa

  
 
    B  0  j
=0
0
Mamy sprzeczność – nierówność dwóch stron równania
dodał Maxwell do
prawa Ampere’a

 

E 

  B  0  j   0


t


 

E 
Obliczymy dywergencję:


  
  
 
    B  0    j   0   E 
t


=0
=?


  
 
1 
E 

 ?
t
t  0  0 t
 0 r
Natężenie prądu
 
I   j  dA
dq
d
I 
   dV
dt
dt V
A
 
d
A j  dA  V dt dV
 
 
 C  dA     C dV
A
 
d
V   j dV  V dt dV
V
 

 j  
t
 

 j  
t


  
1 
1  
E 
   j
t
 0 t
0
otrzymaliśmy wcześniej
Prawo Ampere’a + składnik Maxwella


  
  
 
    B  0    j   0   E  
t


 
1  
  0    j   0   j   0
0


lewa strona = prawa strona
gęstość prądu przewodzenia

 

E 

  B  0  j   0


t


gęstość prądu przesunięcia
S=l
Równania Maxwella w postaci różniczkowej i
całkowej
  
 
  Q
E  Es  EB

E 
E  dA 

 
 0 r

0
A
  Es  0
 
 
 B  0
 B  dA  0

 
B
 E  
dt
A
 
  
 E  dl   dt A B  dA

 
 


E 
  
 I   0  E  dA 

  B  0  j   0
B

d
l


0





t

t



A


Pola statyczne
 

E 
 
 B  0

 
B
 E  
dt

 

E 

  B  0  j   0


t


 0 r
x
 

E 
 0 r
 
 E  0
elektrostatyka
x
 
 B  0
 

  B  0 j
magnetostatyka
Fale elektromagnetyczne
 

E  X
 
 B  0
 0 r

 
B
 E  
dt

 

E 

  B  0  X
j  0


t


Założenie – nie ma ładunków i prądów
 
 E  0
 
 B  0

 
B
 E  
dt 
 
E
  B  0 0
t
Fala elektromagnetyczna spełnia równania:
 1
 E 2
c
 1
2
 B 2
c
2

 E
0
2
t

2
 B
0
2
t
2
c
1
0 0
prędkość fali elektromagnetycznej
  
E Bc
Pole elektryczne ma tylko składową Ey, pole magnetyczne ma
tylko składową Bz, fala rozchodzi się w kierunku osi x.
E y  f ( x, t ),
Bz  f ( x , t )
Monochromatyczna fala płaska opisana jest równaniami
E y ( x, t )  E0 cosqx  t   
Bz ( x, t )  B0 cosqx  t   
2Ey
2

1 Ey
 2
0
2
2
x
c t
 2 Bz 1  2 Bz
 2
0
2
2
x
c t
c

q

 
B
 E  
dt

i
 

 E 
x
0

j

y
Ey

k
   E y
 i  
z
 z
0

E y ( x, t )   E0 q sin qx  t   
x

 Bz ( x, t )   B0 sin qx  t   
t
   E y
  k 
  x



=0
E0 q  B0

E0

c
q B0

 
E
  B  0 0
t

i
  
 B 
x
0

j

y
0

k
  Bz   Bz 
  j  
 i 

z
 y   x 
Bz
=0

 Bz ( x, t )  B0 q sin qx  t   
x

E y ( x, t )  E0 sin qx  t   
t
B0 q   0 0 E0

B0 1
 0 0 

q E0 c

c
c
1
 0 0
Potencjał wektorowy
Potencjał pola elektrostatycznego pochodzącego od ciągłego rozkładu
ładunku w danym punkcie pola jest równy
r12
dV2
1(x1,y1,z1)
 (1) 
1
40

 (2)dV2
r12
Związek natężenia pola z potencjałem:
2(x2,y2,z2)


E  
Czy pole magnetyczne możemy również opisać takim potencjałem?
 
 E  0
ale
 
 B  0
lub
 
 B  0
Wektor indukcji magnetycznej możemy przedstawić jako rotację
pewnego wektora
  
B   A
Przez analogię do pola elektrostatycznego nazwiemy go potencjałem
wektorowym.
Prawo Gaussa dla magnetyzmu jest spełnione:
 
B  0


  
  A  0
zawsze!!!
Ponieważ
 

  B  0 j


  

    A  0 j

i
   
B   A 
x
Ax

j

y
Ay

k


z
Az
 Az Ay   Ax Az   Ay Ax 
  j 

 i 



  k 
y
z  
z 

x   x
y 


 


 

By
Bx


  
  A 

i

x
Az Ay

y
z
Bz

j

y
Ax Az

z
x
Ay

k

z
Ax

x
y
Składowa x równania


  

    A  0 j
  Ay Ax    Ax Az 

  


  0 j x
y  x
y  z  z
x 
Zakładamy, że można zmienić kolejność różniczkowania:
 2 Ax  2 Ax  Az  Ay
 2  2 

 0 j x
y
z
x z x y
 2 Ax  2 Ax  2 Ax  2 Ax  Az  Ay

 2 



 0 jx
2
2
2
y
z
x

x
x z x y

 
0
 2 Ax  2 Ax  2 Ax  2 Ax  Az  Ay

 2 



 0 jx
2
2
2
y
z
x

x
x z x y

 
0


  2 Ax  2 Ax  2 Ax    Ax Az Ay 

  2 



 0 jx
2
2 
y
z
x  x  x
z
y 












 
 A


 2 Ax
może być dowolna, w
szczególności = 0
Spośród możliwych rozwiązań rozważymy tylko takie, dla których
 
 A  0
Otrzymamy więc:
 2 Ax  2 Ax  2 Ax
 2  2   0 j x
2
y
z
x
Równanie to ma postać taką jak równanie Poissona dla potencjału
pola elektrostatycznego
 2  2  2

 2  2 
2
x
y
z
0
 (1) 
1
40

 (2)dV2
r12
rozwiązanie równania
Poissona
Składowa x potencjału wektorowego musi spełniać zależność
0
A( x1 , y1 , z1 ) 
4

j x ( x2 , y2 , z 2 )dV2
r12
Dla pozostałych składowych otrzymamy podobne związki. Potencjał
wektorowy możemy zapisać w postaci wektorowej

0
A( x1 , y1 , z1 ) 
4

V

j ( x2 , y2 , z 2 )dV2
r12
Całkowanie przeprowadza się po całej objętości, w której płyną prądy
wytwarzające pole.
Jeśli znamy rozkład prądów wytwarzających pole możemy obliczyć
potencjał wektorowy a następnie – obliczając rotację potencjału –
indukcję pola magnetycznego.