Precesja P ( |P|=P=mg ) ω LR ∆ω xyz

Precesja
Ruch precesyjny jest skutkiem działania momentu sił na wirującą bryłę. Obliczmy okres
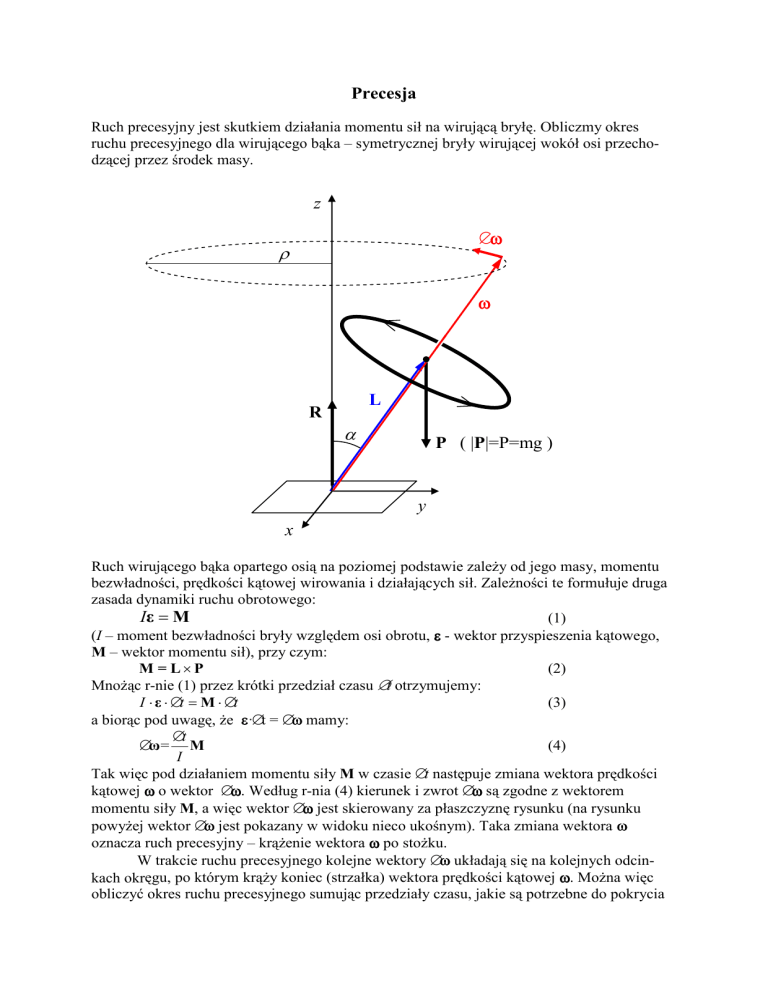
ruchu precesyjnego dla wirującego bąka – symetrycznej bryły wirującej wokół osi przechodzącej przez środek masy.
z
∆ω
ω
ρ
ω
L
R
α
P ( |P|=P=mg )
y
x
Ruch wirującego bąka opartego osią na poziomej podstawie zależy od jego masy, momentu
bezwładności, prędkości kątowej wirowania i działających sił. Zależności te formułuje druga
zasada dynamiki ruchu obrotowego:
Iε = M
(1)
(I – moment bezwładności bryły względem osi obrotu, ε - wektor przyspieszenia kątowego,
M – wektor momentu sił), przy czym:
M = L×P
(2)
Mnożąc r-nie (1) przez krótki przedział czasu ∆t otrzymujemy:
I ⋅ ε ⋅ ∆t = M ⋅ ∆t
(3)
a biorąc pod uwagę, że ε·∆t = ∆ω
ω mamy:
∆t
∆ω = M
(4)
I
Tak więc pod działaniem momentu siły M w czasie ∆t następuje zmiana wektora prędkości
kątowej ω o wektor ∆ω
ω. Według r-nia (4) kierunek i zwrot ∆ω
ω są zgodne z wektorem
momentu siły M, a więc wektor ∆ω
ω jest skierowany za płaszczyznę rysunku (na rysunku
powyżej wektor ∆ω
ω jest pokazany w widoku nieco ukośnym). Taka zmiana wektora ω
oznacza ruch precesyjny – krążenie wektora ω po stożku.
W trakcie ruchu precesyjnego kolejne wektory ∆ω
ω układają się na kolejnych odcinkach okręgu, po którym krąży koniec (strzałka) wektora prędkości kątowej ω. Można więc
obliczyć okres ruchu precesyjnego sumując przedziały czasu, jakie są potrzebne do pokrycia
całego okręgu (linia przerywana) odcinkami o długości |∆ω
ω|. Liczba takich odcinków na
ω|:
okręgu wynosi tyle, co stosunek długości okręgu do |∆ω
2πρ 2πω sin α
liczba odcinkow =
=
(5)
∆ω
∆ω
Każdemu z tych odcinków odpowiada czas ∆t. Zatem na pełny okres precesji T mamy
wyrażenie:
2πω sin α
2πω sin α
T = (liczba odcinkow) ⋅ ∆t =
⋅ ∆t =
⋅ ∆t
(6)
∆t
∆ω
M
I
Biorąc pod uwagę że M=|M|=mgL·sinα, otrzymujemy ostatecznie:
2π I ω
T=
(7)
mgL
Wprowadzając prędkość kątową precesji Ω możemy zapisać:
2π mgL
Ω=
=
(8)
T
Iω
Prędkość kątowa precesji jest więc niezależna od kąta odchylenia bąka od pionu (α) i
odwrotnie proporcjonalna do jego momentu bezwładności i prędkości kątowej wirowania.
Pytanie dodatkowe: jaki jest kierunek i wartość wektora momentu pędu bryły J,
gdy bryła wykonuje jednocześnie ruch wirowy (ω) i ruch precesyjny (Ω) ?
Inne, bardziej sformalizowane matematycznie rozwiązanie powyższego zadania jest
przedstawione poniżej.
Wprowadźmy współrzędne środka masy X, Y, Z, które zarazem stanowią składowe wektora L
(położenia środka masy) w układzie kartezjańskim na rysunku powyżej:
L = [ X ,Y , Z ]
(1a)
Z kolei wektor ciężaru bąka P ma postać:
P = [ 0,0, − mg ]
(2a)
Równanie (1) z wektorem przyspieszenia kątowego ε wyrażonym przez jego składowe εx, εy,
εz, można teraz jawnie zapisać w postaci:
 I ε x , I ε y , I ε z  = [ X , Y , Z ] × [ 0,0, − mg ]
(3a)
Obliczając iloczyn wektorowy po prawej stronie i zastępując składowe wektora ε po lewej
stronie pochodnymi odpowiednich składowych wektora ω mamy:
 I ωɺ x , I ωɺ y , I ωɺ z  = [ − mgY , mgX ,0]
(4a)
Przyrównując do siebie odpowiednie składowe wektorów po lewej i prawej stronie tego
równania otrzymujemy układ równań:
I ωɺ x = − mgY
I ωɺ y = mgX
(5a)
I ωɺ z = 0
Są to trzy równania różniczkowe, w których niewiadomymi są funkcje ωx(t), ωy(t), ωz(t).
Z trzeciego z tych równań wynika, że ωz nie zależy od czasu, a więc rzut wektora ω na oś z
układu współrzędnych pozostaje stały.
Zajmijmy się pierwszymi dwoma równaniami. Ponieważ wektory L oraz ω są współliniowe,
to można zapisać ω w postaci:
ω
L
ω = ⋅ω = ⋅ω
(6a)
ω
L
(wykorzystaliśmy tu fakt, że ten sam wektor jednostkowy można utworzyć z ω jak i z L).
Zróżniczkujmy obie strony powyższej równości względem czasu biorąc pod uwagę
niezmienną wartość prędkości kątowej wirowania ω, a otrzymamy:
Xɺ
Yɺ
Zɺ
Lɺ
ɺ = ⋅ω
ω
czyli: ωɺ x = ω ωɺ y = ω ωɺ z = ω
L
L
L
L
Wstawiając pochodne ωx oraz ωy do równań (5a) otrzymujemy:
Xɺ
I ω = − mgY
L
(7a)
Yɺ
I ω = mgX
L
Jest to układ równań różniczkowych, z którego można wyznaczyć funkcje X(t) i Y(t), czyli
współrzędne środka masy bąka. Wyznaczając z drugiego z tych równań funkcję X(t) a
następnie jej pochodną względem czasu:
Iω ɺ
I ω ɺɺ
X =
Y
→
Xɺ =
Y
mgL
mgL
i podstawiając jej pochodną do pierwszego r-nia w układzie (7a) otrzymujemy:
2
 mgL 
Yɺɺ = − 
 Y
 Iω 
Po wprowadzeniu oznaczenia:
mgL
Ω=
Iω
ostateczna postać równania na Y(t) jest:
(8a)
(9a)
Yɺɺ = −Ω 2Y
(10a)
Jest to równanie, którego rozwiązaniem są funkcje sin(Ωt) oraz cos(Ωt), a ogólnie:
Y ( t ) = A sin ( Ωt + ϕ )
Postać funkcji Y(t) mówi, że środek masy bąka wykonuje ruch periodyczny wzdłuż osi Y
układu wspólrzędnych z częstością kołową Ω − tą samą, którą otrzymaliśmy prostszą metodą
w postaci wzoru (8).
Podobnie, wyznaczając z pierwszego r-nia (7a) funkcję Y, różniczkując ją i wstawiając jej
pochodną do drugiego równania otrzymamy równanie analogiczne do (10a) ale dla funkcji X:
Xɺɺ = −Ω 2 X
Dalsza analiza rozwiązań Y(t) i X(t) prowadzi do wniosku, że współrzędne środka masy
zależą od czasu w sposób następujący:
Y ( t ) = A sin ( Ωt + ϕ )
X ( t ) = A cos ( Ωt + ϕ )
a więc środek masy o współrzędnych X i Y krąży po okręgu o promieniu A z prędkością
kątową Ω.