Sukając wzoru na elastyczność możemy odwołać się do nachylenie
advertisement
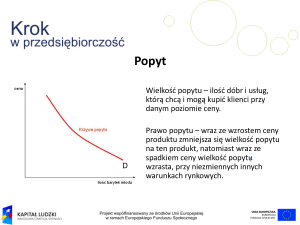
Szukając wzoru na elastyczność możemy odwołać się do nachylenie krzywej D, tj q . Niemniej napotykamy tu problem, np. jak p porównać wzrost popytu o 10 samochodów do spadku ceny samochodów o 500 zł. Kategorie popyt i cena mają inne jednostki, dlatego q pq q q posłużymy się wartościami względnymi , inaczej . Dla liniowej funkcji popytu w formie q a bp , = - b , co p qp p p p pq q można wykorzystać w obliczeniach E , gdzie w wcześniejszym wzorze , wymienimy = - b. Ostatecznie E = b , czyli q qp p bp bp , a gdy q zastąpimy częścią wzoru funkcji popytu ( q a bp ), wtedy E = . q a bp Przychód w takich warunkach będzie maksymalizowany jeśli E = bp = -1. Gdy rozwiążemy równanie względem p, to okaże się, a bp a bp . Jeśli będziemy obliczać q wychodząc od E = = -1, a z wcześniejszego równania q a bp wyliczymy p, wtedy 2b q a podstawiając do poprzedniego wzoru i rozwiązując równanie względem q otrzymamy wynik q = . Reasumując jeśli mamy do 2 a a czynienia z funkcją liniową popytu, to cena maksymalizująca PC wynosi p = , zaś ilość q = . 2b 2 że p = Sytuacja bardziej się komplikuje, jeśli będziemy rozważać inne funkcje, wtedy przydaje się rachunek różniczkowy, ponieważ wyrażenie q określa nam nachylenie funkcji a to oznacza, że możemy posłużyć się pochodną funkcji, aby tę wielkość wyznaczyć. p Zadanie 1. Dla poniższych funkcji popytu określ wzór na elastyczność: a) q = 30 – 6p; b) q = 60 – p; c ) q = 12 – 3p; d) q = 10-p; f) q = a – bp; g) *q = 40p-2; h)*q = Ap-b; i)*q = (p+3)-2; g)*q = (p+a)-b *dla zaawansowanych W przypadku liniowych funkcji określ p i q maksymalizujące PC Zadanie 2. W miejscowości Sokółka mieszkają konsumenci, którzy posiadają albo maluchy albo duże Land Rovery (LR). Popyt na benzynę dla właściciela malucha wyraża się wzorem q = 20-5p, dla p 4 zł i q=0, dla p 4 zł. Popyt właściciela LR wyraża się wzorem q = 15 -3p, dla p 5 zł, i q>0 dla p>5. (ilość w litrach na tydzień, cena w zł). W Sokółce mieszka 100 właścicieli maluchów i 50 właścicieli LR. a) Jeśli p = 3zł, to na jaką ilość zgłosi zapotrzebowanie właściciel malucha a na jaką właściciel LR? b) Na jaką ilość zgłoszą zapotrzebowanie wszyscy właściciele maluchów a na jaką właściciele LR? c) Jaka jest ilość całkowita zapotrzebowania na benzynę? d) Jeśli cena benzyny kształtuje się na poziomie 1 zł/l , to o ile spadnie popyt jeśli cena wzrośnie o 10 groszy? Zadanie 3. Jaka jest funkcja odwrotna do funkcji popytu, jeśli funkcja popytu jest dana wzorem q= 100-0,5p ? Zadanie 4. Jeśli funkcja popytu określona jest wzorem q= 12- 2p, to jaka cena będzie maksymalizować przychód? Zadanie 5. Jeśli funkcja popytu wyraża się wzorem q = 100/p, to przy jakiej cenie PC będzie maksymalny? Zadanie 6. Funkcja odwrotna popytu na korepetycje wyraża się wzorem p = 20- q A) przy jakiej cenie PC będzie maksymalny B) ile przy tej cenie będzie można sprzedać korepetycji? Zadanie 7. Funkcja popytu na bilety na typowy mecz piłkarski na stadionie Valencia Mestalla wynosi q = 200 000 – 10 000p. Stadion ten ma dobrego menedżera, który ustala ceny biletów, aby maksymalizować przychód. Stadion mieści 100 000 widzów. a) określ funkcję odwrotną do funkcji popytu b) napisz wyrażenie na PC (i przychód krańcowy) jako funkcję sprzedanych biletów c) Jaka P maksymalizuje PC? Jaka liczba biletów będzie sprzedana po tej cenie? d) Przy tej liczbie biletów, jaki jest przychód krańcowy oraz elastyczność cenowa popytu? Czy stadion będzie pełny? e) Seria bardzo udanych spotkań piłkarskich doprowadziła do zwiększenia popytu na bilety. Nowa funkcja popytu wygląda następująco: q = 300 000 – 10 000 p. Jaka jest funkcja odwrotna do nowej funkcji popytu? f) Pomijając wielkość stadionu, jaka cena maksymalizowałaby PC? Ile biletów można by było przy tej cenie sprzedać?
