Prąd elektryczny 9.1 Natężenie prądu, wektor gęstości prądu

Wykład 12
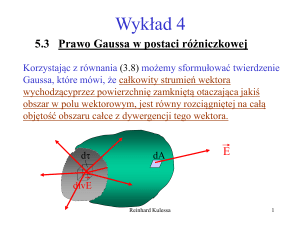
8.10 Gęstość energii pola elektrycznego
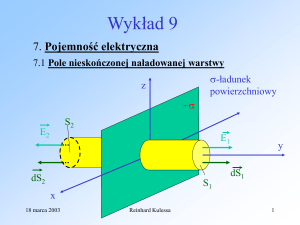
9. Prąd elektryczny
9.1 Natężenie prądu, wektor gęstości prądu
9.2 Prawo zachowania ładunku
9.3 Model przewodnictwa elektrycznego
27 marca 2003 r.
Reinhard Kulessa
1
8.10 Gęstość energii pola elektrycznego
-Q
Rozważmy jednorodne pole elektryczne zawarte pomiędzy
okładkami kondensatora płaskiego naładowanego ładunkiem
Q. Przeniesienie z okładki na okładkę ładunku dQ wymaga
wykonania pracy dW.
A powierzchnia
L
Jeżeli przeniesiemy z ujemnej płyty
ładunek +dQ na dodatnią płytę, to

wykonamy pracę przeciwko polu
+Q
elektrycznemu równą
dQ+
V
 
V
dW  dQ   E  dl  dQ   L  dQ  V
l
L
Na wskutek przeniesienia ładunku z okładki ujemnej
na dodatnią napięcie na kondensatorze wzrośnie o dV.
27 marca 2003 r.
Reinhard Kulessa
2
L

-(Q+dQ)
+(Q+dQ)
Wobec tego dQ = C dV. Możemy
więc napisać:
dW = C V dV .
Po wycałkowaniu, otrzymujemy:
dQ+
V
V+dV
W 
0
1 2 1 Q2
C  V  dV  CV 
2
2 C
Wykonana praca została zmagazynowana w kondensatorze jako
energia potencjalna (W = U ). Może ona zostać wykorzystana do
wykonania pracy przez kondensator.
Czyli,
Pamiętając, że C =0 A/L, a V=L E,
1
2
U
27 marca 2003 r.
2
C V
2
1
U   0  { A  L}  E
2
Reinhard Kulessa
3
Możemy więc wyliczyć gęstość energii pola elektrycznego,
która wynosi:
 
1
U 
 0 E  E
A L 2
Ep
1  
U  DE
2
i dalej:
(8.28)
Ponieważ dowolne pole można na małym obszarze traktować
jako jednorodne, wzór ten stosuje się również do pól
niejednorodnych.
d mikro-objętość pola , którą można
uważać za mały kondensator.
Linie
ekwipotencjalne
27 marca 2003 r.
Reinhard Kulessa
4
Rozważmy dwa zastosowania energii pola elektrycznego.
A). Pomiędzy okładkami kondensatora działają siły, które można
wykorzystać do dokładnego pomiaru napięcia.
Wirtualne rozsunięcie okładek
o dx powoduje zmniejszenie
dx
energii pola. Ładunek spływa z
+Q
V
powrotem do baterii.
x
F
Wiemy, że energia pola jest
-Q
równa
1
2
U

C

V
A
.
2
Pamiętamy, że C = 0 A/x. Otrzymamy więc:
1
A
U   0   V 2
2
x
1
dx
2
dU   0  A  V (  2 )
2
x
27 marca 2003 r.
Reinhard Kulessa
5
Obliczona strata energii dU związana z rozsunięciem okładek o
dx jest równoważona przez wykonana pracę mechaniczną na
rozsunięcie tych okładek.
1
2 dx
 F  dx   0  A  V  2
2
x
Siła działająca pomiędzy płytkami kondensatora jest więc
równa:
1
V2
F  0 A 2
2
x
Wyrażenie to może służyć do dokładnego pomiaru różnic
potencjałów. Służy do tego tzw. Waga Thomsona.
27 marca 2003 r.
Reinhard Kulessa
6
A
Waga Thomsona
L
V
B). Zmiana energii pola elektrycznego może również posłużyć
do wyznaczania stałej dielektrycznej dielektryków ciekłych.
b
x
27 marca 2003 r.
a
Jeśli poziom cieczy podniesie
się o dx wtedy objętość
wypełniona dielektrykiem
wzrasta o a·b·dx.
Reinhard Kulessa
7
Przyrost energii pola elektrycznego wynosi jest równy;
1 2
dU E  E  0  ab  dx  (  1)
2
Praca na podniesie nie poziomu cieczy jest równa:
dWg    g  ab  dx  x
Praca, którą musi wykonać bateria aby dostarczyć dodatkowego
ładunku dQ jest równa: dW  V  dQ  2  dU
B
Z porównania:
E
dWB  dU E  dWg
.
oraz wiedząc, że E=V/a, otrzymujemy następujące wyrażenie na
wysokość słupa cieczy wciągniętej pomiędzy, okładki
2
kondensatora:
1 V 
x
    0 (  1)
(8.30)
2 g  a 
27 marca 2003 r.
Reinhard Kulessa
8
9. Prąd elektryczny
9.1 Natężenie prądu, wektor gęstości prądu
Opuszczamy rozważanie stabilnych rozkładów ładunków i od
tej chwili pozwalamy im się poruszać.
W elektrostatyce:
1. Powierzchnie przewodników są powierzchniami
ekwipotencjalnymi,
2. Ładunki są rozmieszczone na powierzchni i spoczywają,
3. Wewnątrz przewodników natężenie pola E jest równe zero,
Połączmy przewodnikiem dwa naładowane elektroskopy i
zobaczmy co się dzieje.
27 marca 2003 r.
Reinhard Kulessa
9
+Q
-Q
V3
V1
V2
Po połączeniu elektroskopów następuje w krótkim czasie
wyrównanie ładunków. Co natomiast dzieje się z potencjałem?
t=0
V0 = V1 – V2
Przypadek statyczny
2 powierzchnie
ekwipotencjalne
t=
V0 = 0
Przypadek statyczny
1 powierzchnia
ekwipotencjalna
t=t’
V0 maleje
27 marca 2003 r.
Przypadek niestatyczny Potencjał zależy od
miejsca pomiaru
Reinhard Kulessa
10
Oznacza to, że w czasie przepływu ładunku mamy do czynienia
ze spadkiem potencjału, czyli, że w przewodniku pojawia się
pole elektryczne.
Przepływ ładunków przewodniku zarówno dodatnich jak i
ujemnych nazywamy prądem elektrycznym.
Na rysunku na poprzedniej stronie poruszają się elektrony i
zachodzi to z prawej strony na lewą.
Prąd elektryczny charakteryzowany jest przez swoje natężenie,
które definiujemy jako całkowity ładunek przepływający przez
daną powierzchnię w jednostce czasu.
dQ
I 
dt
(9.1)
Jednostką natężenie prądu jest amper. [1 A=1C/1sek].
27 marca 2003 r.
Reinhard Kulessa
11
Do pomiaru natężenia prądu wykorzystuje się wszelkie efekty
wywoływane przez płynący prąd. Nośnikami prądu w metalach
są elektrony, a w gazach i elektrolitach – jony.
dA
A
Ważną wielkością
charakteryzującą prąd
elektryczny jest wektor
j
gęstości prądu j. Jego
kierunek jest określony
przez ruch ładunków dodatnich.
Wartość wektora j ,| j | jest równa ładunkowi
przepływającemu przez jednostkę powierzchni
dA prostopadłej do j na jednostkę czasu.
Przez element powierzchni dA przepływa w czasie dt ładunek
27 marca 2003 r.
Reinhard Kulessa
12
 
 
dQ  j  dA  cos( j , dA)  dt  j  dA  dt

dQ
dI
| j |

dAn dt dAn
Przy czym
(9.2)
(9.3)
 
dAn  dA cos( j , dA)
Jednostką gęstości prądu w układzie SI jest [A/m2].
W oparciu o wzór (9.2) znajdujemy na natężenie prądu
przepływającego przez całą powierzchnię A wyrażenie;
dQ
I 

dt
27 marca 2003 r.

A
Reinhard Kulessa
 
j  dA
(9.4)
13
9.2 Prawo zachowania ładunku
W jaki sposób sformułować prawo zachowania ładunku, kiedy
mamy przepływ prądu.
Zgodnie z wzorem (9.4) wiemy ile na
dA j
j
sekundę przepływa ładunku przez
j
całą powierzchnie przewodnika,
mianowicie
 


A
j
j
A
27 marca 2003 r.
W oparciu o twierdzenie Gaussa
mamy:
j
j
j  dA

A
  Gauss

j  dA  div j d
Reinhard Kulessa

14

Na jednostkę czasu w przewodniku ubywa 
t
ładunku.
  d
Bilans ładunku wynosi więc:


 div j d   t   d
(9.5)
Wyrażenie to jest ważne dla każdej objętości , a więc również
dla objętości d. Otrzymujemy więc równanie, które
nazywamy równaniem ciągłości:
 
div j 
0
t
(9.6)
Dla prądu o stałym natężeniu I=0 wektor gęstości też jest

niezależny od czasu. div j  0 Tyle samo ładunku wpływa
co wypływa z danej
objętości.
27 marca 2003 r.
Reinhard Kulessa
15
9.3 Model przewodnictwa elektrycznego
Pamiętamy, że nośnikami ładunków mogą być elektrony, jak
również jony dodatnie i ujemne. Najlepszymi przewodnikami są
metale w których znajduje się wiele swobodnych elektronów.
Zastanówmy się nad mechanizmem przewodzenia prądu w
metalicznym przewodniku.
• Każdy atom siatki oddaje średnio jeden elektron do całej sieci
(elektrony przewodnictwa). Elektrony te zachowują się jak gaz.
Gęstość tego gazu jest bardzo wysoka. Do elektronów jako
fermionów stosuje się statystyka Fermiego- Diraca.
• Przyjmuje się, że prędkość elektronu przed zderzeniem nie
wpływa na prędkość po zderzeniu. Oznacza to, że zderzenia
„wymazują pamięć” elektronów. Oznaczmy średni czas
pomiędzy dwoma kolejnymi zderzeniami przez .
27 marca 2003 r.
Reinhard Kulessa
16
Co zachodzi w czasie przepływu prądyw przewodniku. W
przewodniku istnieje pole elektryczne E . Elektrony w czasie
ruchu w polu elektrycznym zderzają się głównie z elektronami
związanymi w atomach. Tor przypadkowego elektronu jest
przedstawiony na poniższym rysunku.
E
Jądro
atomowe


Na elektrony działa siła F  e  E .
27 marca 2003 r.
Reinhard Kulessa
17
Na ukierunkowany ruch elektronów pod wpływem pola
elektrycznego nakładają się izotropowe ruchy termiczne
E
1/
vx0
v0
1/
2
b
2
v2
v1
1/
x0
2
b
2
2b
2
x1
x2
x
x3
Pomiędzy kolejnymi zderzeniami następującymi po średnim czasie
 elektron porusza się w kierunku osi x ruchem jednostajnie
przyśpieszonym.
27 marca 2003 r.
Reinhard Kulessa
18
Ruch elektronu odbywa się zgodnie z II zasada dynamiki
Newtona,
.
d 2x
m
 eE
2
dt
d 2x
eE
b
2
dt
m
Licząc kolejne odcinki przebyte między zderzeniami, otrzymujemy,
x1  x0   v x 0  12 b  2
x2  x1   v x1  12 b  2
x N  x N 1   v x ( N 1)  12 b  2
Sumujemy te równania po N zdarzeniach, przy czym N>>1.
27 marca 2003 r.
Reinhard Kulessa
19
W wyniku otrzymujemy:
N
x N  x0    v xi  N 12 b  2
i 0
Ze względu na izotropowy rozkład kierunków ruchów termicznych,
pierwszy wyraz po prawej stronie jest równy zero, gdyż tyle samo
cząstek może mieć prędkości –vx jak i +vx. Średnia prędkość
elektronów w kierunku x (prędkość dryfu) jest więc równa:

x N  x0 1
e 
 vD  
 2 b    E.
N
m 2
Zdefiniujmy jeszcze czas relaksacji jako <R> = /2. Wtedy


e
vD 
R E
m
27 marca 2003 r.
Reinhard Kulessa
(9.7)
20
Ruchliwością nośników prądu nazywamy:
e
  R
m

vD
 
E
.
Mimo, że ruch pod wpływem siły eE powinien być przyśpieszony,
ze względu na występujące zderzenia, nie ma przyśpieszenia.
Średnia prędkość dryftu jest stała. Ruch elektronu wygląda tak,
jakby istniała siła tarcia. Wpływ zderzeń na ruch ilustruje poniższa
animacja.
W rzeczywistości poprzez zderzenia sieci dostarczana jest
energia, tzw. „ciepło Joule’a” . Cdn.
27 marca 2003 r.
Reinhard Kulessa
21
Równanie (9.7) możemy też interpretować następująco. W sieci
w której poruszają się elektrony działa na nie poza siłą

przyspieszającą F = eE, również siła tarcia

m v
R
Zachodzi więc równowaga F + R =0.
Z tego faktu wynika jednostajny ruch elektronów.
D
R
.
Na podstawie definicji wektora gęstości prądu (r. (9.3) ), oraz
średniej prędkości dryfu, możemy wyrazić wektor gęstości prądu
jako:

dAn
dV
dI
dl = <vD> dt
27 marca 2003 r.
dI
dQ dl
j 

 
dAn dAn dt dl

dQ 
 vD   vD
d V
Reinhard Kulessa
22