Sformułowanie Kelvina – Plancka

Wykład 7
5.13 Mikroskopowa interpretacja ciepła i pracy.
5.14 Entropia
5.15 Funkcja rozdziału
6 II zasada termodynamiki
6.1 Sformułowanie Clausiusa oraz Kelvina-Plancka II zasady
termodynamiki
6.2 Procesy odwracalne oraz cykle
2011-04-11
Reinhard Kulessa
1
5.13 Mikroskopowa interpretacja ciepła i pracy.
Pamiętamy, że I zasadę termodynamiki dla układu
zamkniętego możemy napisać w następującej postaci:
dU  d ' Q  d ' W
(5.42)
Zgodnie z równaniem (5.20) U  i i N i  const zmiana
energii wewnętrznej może zostać napisana jako:
dU   i dN i   N i d i
i
(5.43)
i
Rozważmy prosty układ nie oddziaływujących cząstek.
Załóżmy, że jedynym oddziaływaniem dla tego układu może
być praca związana z kompresją. Z rozważań kwantowomechanicznych można pokazać, że dozwolone stany energii
translacyjnej takiego układu są proporcjonalne do V-2/3 , gdzie
V jest objętością układu.
2011-04-11
Reinhard Kulessa
2
Dla stałej objętości stany energetyczne są ustalone. Możemy
więc napisać, że Єi = f(V), oraz
d i
dU   i dN i   N i (
) dV
dV
i
i
(5.44)
Zastanówmy się co można wywnioskować z tego równania jeśli
zastosujemy je do kwazistatycznego procesu któremu poddamy
ściśliwą substancję, której objętości nie zmienimy.
Praca na ściskanie tej substancji jest więc równa zeru. Energia
wewnętrzna układu musi więc wzrosnąć kosztem
oddziaływania cieplnego. Stwierdzimy wobec tego, że
d ' Q   i dN i
(5.45)
i
Jeśli natomiast wykonamy pracę na sprężenie układu lecz bez
wymiany ciepła, wtedy
2011-04-11
Reinhard Kulessa
3
d i
d 'W   Ni (
) dV   N i d i
dV
i
i
(5.46)
Omówiony proces kwazistatyczny możemy zinterpretować w
następujący sposób w oparciu o model mikroskopowy.
Dostarczanie ciepła przy zachowaniu stałej objętości
uwidacznia się w zmianie populacji poziomów Ni, , lecz
wartości energii dozwolonych stanów energetycznych nie
zmieniają się.
Dodanie energii cieplnej powoduje wzrost populacji poziomów
o wyższych energiach kosztem obniżenia populacji stanów o
niższych energiach.
Natomiast adiabatyczne sprzężenie substancji nie zmienia
populacji poziomów, powoduje natomiast wzrost ich energii.
2011-04-11
Reinhard Kulessa
4
Sytuacja ta jest przedstawiona na poniższych rysunkach.
Dodanie ciepła
Є
Єi
Adiabatyczne sprężenie
Stan
końcowy
i
Stan
końcowy
Stan
początkowy
Stan
początkowy
Ni
Ni
2011-04-11
Reinhard Kulessa
5
5.14 Entropia
Pamiętamy z naszych rozważań jak przytłaczająca jest
dominacja najbardziej prawdopodobnego stanu. Będziemy
wobec tego chcieli określić maksymalne prawdopodobieństwo
termodynamiczne max jako makroskopową własność układu.
Dla wygody wybierzmy ln max , a nie samo max i
zdefiniujmy;
(5.47)
S  k ln  max .
k jest wielkością stałą, a S jest makroskopową własnością
stanu równowagi zwaną entropią.
Dla dużej liczby cząstek stany reprezentowane przez , inne
niż max , są znacznie mniej prawdopodobne, lecz wciąż
przedstawiają możliwy stan układu. Dla takiego stanu
S  k ln 
2011-04-11
Reinhard Kulessa
.
(5.48)
6
Porównanie dwóch ostatnich równań wskazuje na to, że gdy
izolowany układ (N = U = const), dąży do swojego najbardziej
prawdopodobnego stanu, jego entropia dąży do swojej
maksymalnej wartości. Równocześnie jest mało prawdopodobne,
że entropia osiągnie wartość mniejszą niż maksymalną, ze
względu na dominujący charakter maksymalnego
prawdopodobieństwa max. Należy zaznaczyć, że zmniejszenie
entropii nie jest niemożliwe, jest prawdopodobne.
W układzie izolowanym zachowanie się entropii jest inne niż
zachowanie energii wewnętrznej. Energia wewnętrzna w układzie
izolowanym zgodnie z I zasadą termodynamiki nie może się
zmieniać.
Inne sformułowanie tego co powiedzieliśmy do tej pory, jest takie,
że w każda zmiana układu izolowanego powoduje
najprawdopodobniej wzrost entropii, czyli
Sizol  0
2011-04-11
Reinhard Kulessa
(5.49)
7
jest najbardziej prawdopodobne.
Równanie (5.49) jest jednym ze sformułowań II zasady
termodynamiki. Problem ten będzie jeszcze tematem naszych
rozważań. Nasza obecna interpretacja tego równania jest taka,
że układ izolowany dąży do stanu o maksymalnej entropii.
5.15 Funkcja rozdziału
Zgodnie z równaniem (5.33) możemy dla rozkładu MaxwellaBolzmanna napisać następującą zależność;
1
  i
N i  gi e
A
,
(5.50)
w której jak pamiętamy, że gi oznacza liczbę stanów
kwantowych posiadających energię Єi.. W modelu klasycznym,
o ciągłym rozkładzie energii możemy napisać:
2011-04-11
Reinhard Kulessa
8
1   i
Ni  e
A
(5.51)
1
  i
N   Ni   e
A i
i
(5.52)
Wiemy, że
Sumę występującą po prawej stronie tego równania nazywamy
sumą stanów lub sumą statystyczną lub funkcją rozdziału Z.
Z 
e
u

(5.53)
i
W oparciu o równania (5.51), (5.52) i (5.53) możemy napisać:
Ni
1   i

e
N
Z
2011-04-11
Reinhard Kulessa
(5.54)
9
Funkcja rozdziału określa nam więc sposób w jaki cząstki są
rozłożone pomiędzy różne dostępne dla nich stany energetyczne.
Pamiętamy tabelę w rozdziale 5.4 podającą stopień degeneracji
stanów energetycznych cząstki posiadającej tylko kinetyczną
energię translacyjną. Możemy w tej chwili policzyć funkcję
rozdziału Z dla poszczególnych poziomów.
Musimy tutaj jednak użyć ogólnej funkcji rozdziału dla
nieciągłego rozkładu poziomów energetycznych. Musimy
posumować po wszystkich stanach energetycznych dostępnych
dla cząstki.
  i
gi e
Z
(5.55)
N   Ni  

A
A
i
i
gdzie
Z   gi e

 i
(5.56)
i
2011-04-11
Reinhard Kulessa
10
Mamy więc dla rozkładu Maxwella-Bolzmanna bez
ograniczenia, że gi = 1 następujące wyrażenie rozkład cząstek
pomiędzy stany Ni ;
Ni
1
  i
 gi e
N
Z
(5.57)
Policzmy w oparciu o równania (5.56) i (5.57) funkcję rozdziału
dla rozkładu translacyjnej energii kinetycznej, którą
rozważaliśmy w Rozdziale 5.4, zakładając, że  = 1. Otrzymamy
wtedy;
Z   gi e

 i
0
 g o e  g1 e

 1
 g2e

 2
 g 3e

 3

i
 1  e 0  3  e 1  6  e 2  10  e 3 
 3.415
2011-04-11
Reinhard Kulessa
11
W oparciu o równanie (5.57) otrzymujemy;
N0
N
N1
N
N2
N
N3
N
1

 0.293
3.415
1.104

 0.323
3.415
0.813

 0.238
3.415
0.498

 0.146
3.415
Ni/N
0.4
0.3
0.2
0.1
0
1
2
3
Єi
W oparciu o równanie (5.55) i (5.56) możemy wyznaczyć stałą
A. Stałą  będziemy w stanie wyznaczyć po dokładniejszej
dyskusji II zasady termodynamiki. Teraz podamy tylko, że;
2011-04-11
Reinhard Kulessa
12
1

kT
.
(5.58)
k jest stałą Boltzmanna i
k = 1.3807 10-23 J/mol·K.
Stała k w definicji entropii (r. (5.47)) jest również stałą
Boltzmanna.
2011-04-11
Reinhard Kulessa
13
6 II zasada termodynamiki
W rozdziale 1.9 podaliśmy kilka sformułowań II zasady
termodynamiki, oraz stwierdziliśmy, że zasada ta określa
kierunek transferu i przemiany ciepła.
Przy omawianiu I zasady termodynamiki stwierdziliśmy, że
wszystkie rodzaje energii są równie użyteczne, żadna z nich nie
jest preferowana, tylko, że dla układu izolowanego musi ona
zostać zachowana.
Możemy jednak rozróżnić różne rodzaje energii, np.. pracę
mechaniczną i energię wewnętrzną, którą można zmienić przez
pracę. Rozróżniamy również ciepło, które definiujemy przez
energię wewnętrzna i pracę.
Z równania (2.14) które mówi o zmianie energii wewnętrznej dla
2011-04-11
Reinhard Kulessa
14
cyklu zamkniętego
 d ' Q   d 'W  0
(6.1)
można by wyciągnąć wniosek, że dwa człony tego równania są
równoważne. II zasada termodynamiki przyjmuje fakt, że
ciepło i praca nie są równoważne i podaje szereg relacji, które
uzupełniają I zasadę w badaniu układów termodynamicznych.
Przypomnijmy sobie te cztery sformułowania. Przyjrzyjmy się
bliżej pierwszemu i czwartemu.
1. Ciepło przepływa od temperatury wyższej do
temperatury niższej, a nie odwrotnie.
Czyli ciało ciepłe ochłodzi się w kontakcie z chłodnym
ciałem a nie odwrotnie.
2011-04-11
Reinhard Kulessa
15
2. Dwa gazy umieszczone w izolowanym naczyniu
wymieszają się jednorodnie w całym naczyniu i nie będą w
stanie spontanicznie się rozdzielić.
3. Bateria rozładuje się przez opornik wydzielając pewną
ilość ciepła, przy czym proces odwrotny jest niemożliwy.
4. Nie jest możliwe skonstruowanie maszyny pracującej
w sposób ciągły przez pobór ciepła z pojedynczego
zbiornika i wykonującej równoważną ilość pracy.
Pierwsze sformułowanie sprowadza się do tego, że np. naczynie
z wodą włożone do lodówki nie zagotuje się, mimo, że z punktu
widzenia zachowania energii jest to możliwe. Przepływ ciepła
odbywa się tylko w jedną stronę, co nie jest wynikiem zasady
zachowania energii.
2011-04-11
Reinhard Kulessa
16
Stwierdzenie 4 mówi o niemożności zbudowania perpetuum
mobile drugiego rodzaju.
Perpetuum mobile pierwszego rodzaju byłoby urządzeniem, które
wytwarza energię bez brania pod uwagę I zasady termodynamiki.
Konkludując, możemy powiedzieć, że II zasada
termodynamiki przyjmuje jednokierunkowy przepływ ciepła
i pewne określone typy przemiany energii.
Będziemy chcieli sformułować II zasadę termodynamiki
przez podanie zależności analitycznych, bazując na
argumentach makroskopowych i przyjmując czwarte
sformułowanie jako doświadczalny aksjomat.
2011-04-11
Reinhard Kulessa
17
6.1 Sformułowanie Clausiusa oraz Kelvina-Plancka II zasady
termodynamiki
Sformułowanie Clausiusa:
T2
Nie można skonstruować
urządzenia działającego
cyklicznie, którego
jedynym efektem będzie
transport ciepła od ciała
zimniejszego do
cieplejszego.
T2 > T1
Q1 = Q2
Q2

Q1
T1
2011-04-11
Reinhard Kulessa
18
Sformułowanie Kelvina –
Plancka:
Nie można skonstruować
urządzenia działającego
cyklicznie, którego jedynym
efektem jest produkcja pracy
i wymiana ciepła z
pojedynczym zbiornikiem.
T

Q=W
W
2011-04-11
Reinhard Kulessa
19
6.2 Procesy odwracalne oraz cykle
Zdefiniujmy najpierw proces kwazistatyczny. Jest to proces
przebiegający tak wolno, że układ stale pozostaje dowolnie blisko
stanu równowagi.
Kiedy proces można nazwać odwracalnym?
Otóż jeżeli weźmiemy gaz w cylindrze, zauważymy, że
kwazistatyczne rozprężanie tego gazu związane jest z wykonaniem
pracy i oddaniem ciepła. Jeśli jesteśmy w stanie przywrócić
warunki początkowe przez dodanie dokładnie tej samej ilości
ciepła, oraz wykonanie tej samej pracy, to gaz w cylindrze możemy
sprężyć do warunków początkowych. Można więc powiedzieć, że
proces kwasistatyczny jest procesem odwracalnym.
Inaczej mówiąc proces odwracalny jest to taki proces, po zajściu
którego można przywrócić warunki początkowe tylko przez
narzucenie warunku ograniczającego usuniętego na początku
procesu.
2011-04-11
Reinhard Kulessa
20
I jeszcze jedno sformułowanie:
Jeśli jesteśmy w stanie przeprowadzić proces tak, aby nie
była naruszone II zasada termodynamiki, to mówimy, że
proces jest odwracalny.
Procesem nieodwracalnym nazywamy proces, który nie jest
odwracalny.
Cyklem odwracalnym nazywamy ciąg następujących po sobie
procesów odwracalnych takich, że układ w sposób
periodyczny wraca do stanu początkowego.
2011-04-11
Reinhard Kulessa
21
T
T2
Q
Q=W

T2 > T1
T1
W
Konwersja pracy w ciepło
jest procesem
nieodwracalnym.
Sytuacja odwrotna narusza
sformułowanie KelvinaPlancka II zasady
termodynamiki
2011-04-11
Transport ciepła przez
skończoną różnicę
temperatury jest procesem
nieodwracalnym.
Sytuacja odwrotna narusza
sformułowanie KelvinaPlancka II zasady
termodynamiki
Reinhard Kulessa
22
Należy jeszcze zdefiniować cykl mocy, czyli cykl
dostarczający pracę kosztem dostarczanego ciepła, oraz cykl
chłodniczy, który kosztem dostarczanej pracy oddaje ciepło.
Odwracalny cykl mocy może zostać zamieniony na odwracalny
cykl chłodniczy przez odwrócenie strumienia ciepła i pracy.
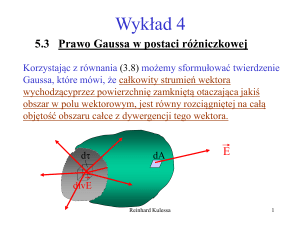
Równoważność sformułowania Clausiusa ze sformułowaniem
Kelvina-Plancka II zasady termodynamiki możemy pokazać
następująco.
Załóżmy, że jest możliwy transfer ciepła wbrew stwierdzeniu
Clausiusa, czyli bezpośrednio z chłodnicy do zbiornika ciepła.
Do tego procesu możemy dodać odwracalny silnik taki jak na
środkowym obrazku. Wynikiem dodania takich procesów jest
powstanie silnika, który wykonuje pracę korzystając tylko z
jednego zbiornika ciepła. A taki proces jest wykluczony przez
2011-04-11
Reinhard Kulessa
23
sformułowanie Kelvina-Plancka II zasady termodynamiki
T2
Q2
T2
T2
Q2
+

W=Q2-Q1
T1
T1
=

W=Q2-Q1
T1
Q2Q1
Pokazaliśmy więc, że złamanie sformułowania Clausiusa II
zasady termodynamiki pociąga za sobą złamanie
sformułowania Kelvina – Plancka II zasady termodynamiki.
2011-04-11
Reinhard Kulessa
24
Dla kompletu zdefiniujmy
sobie jeszcze cykl chłodzący.
T2
Q2

W=Q2-Q1
Q1
T1
2011-04-11
Jeśli chodzi o konwencję
znakową dla ciepła i pracy,
to mówimy:
Energia dodana do systemu
=
Energia akumulowana w
systemie
+
Energia usunięta z systemu.
Reinhard Kulessa
25