Zależność pomiędzy magnetyzacją M a prądem

Wykład 19
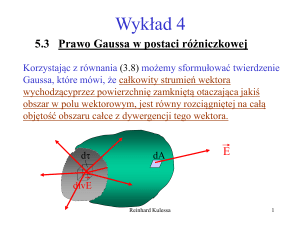
14.4 Siły wynikające z prawa Lorentza i Biota-Savarta c.d.
14.5 Prądy polaryzacyjne w dielektrykach.
15. Magnetyczne własności materii
15.1 Momenty magnetyczne atomów i cząsteczek
15.2 Zależność pomiędzy magnetyzacją M a prądem
cząsteczkowym jmol.
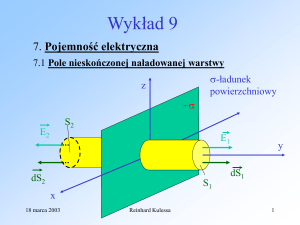
15.3 Wektor natężenie polamagnetycznego H.
15.4 Zdolność magnetyzacji materii
Reinhard Kulessa
1
C). Siła działająca pomiędzy równoległymi przewodnikami
I
F
F
W miejscu, gdzie znajduje się
przewodnik I2 wartość indukcji
magnetycznej jest równa
 0 2 I1
B (r0 ) 
4 r0
I1
I
I2
dF
I
F
F
dl
B(r0)
r0
Reinhard Kulessa
2
Poniżej mamy przedstawiony widok linii indukcji wokół
przewodników.
I2
I1
x
F
F
Silne pole B
Rysunki:D. [email protected]
I1
F I2
F
Słabe pole B
Reinhard Kulessa
3
Siła działająca na element długości przewodnika I2 wynosi
zgodnie z prawem Faraday’a:
 0 2 I1 I 2
dF  I 2 dl B 
dl
4 r0
.
Siła działająca na jednostkę długości przewodnika wynosi;
dF  0 2 I1 I 2
F 

dl 4 r0
'
(14.19)
Na podstawie równania (14.19) stwierdzamy, z gdy w obydwu
przewodnikach odległych od siebie o 1 m płynie prąd o
natężeniu 1A, działa pomiędzy nimi siła 2·10-7 N/m
Reinhard Kulessa
4
D). Moment obrotowy pętli z prądem
F+
MD
1/2b
A
.

a
B
B
b sin
+
Umieszczamy ramkę z
prądem o natężeniu I w
polu indukcji magnetycznej
I
skierowanej prostopadle do
Foś
pokazanej osi ramki. Na
odcinki równoległe do osi
ramki działa siła Lorentza. Dwie działające siły tworzą parę sił z
momentem obrotowym MD.
Reinhard Kulessa
5
Siła działa na odcinki ramki równoległe do osi obrotu i jest ona
równa:
F  I a B .
Moment obrotowy MD stara się ustawić powierzchnię ramki A
równolegle do wektora indukcji magnetycznej B .

| M D |  F (    ) b sin   I ab sin   B
 
Iloczyn ab sin   B można przedstawić jako | A  B | .
Ponieważ MD ⊥ A i B możemy napisać:
  


M D  I  A  B  pM  B
(14.20)
Równanie to jest słuszne dla każdej pętli, gdyż zawsze możemy ją
rozłożyć na odcinki prostopadłe i równoległe do osi obrotu.
Reinhard Kulessa
6
Ostatni przykład ma bardzo szerokie zastosowania m.in. w
przyrządach pomiarowych z ruchomą szpulą, silnikach prądu
stałego, oraz przy magnetyzowaniu materii.
Oddziaływanie pomiędzy poruszającymi się ładunkami a
wektorem indukcji magnetycznej ma również zastosowanie w tzw.
Kole Barlow’a oraz w pompach elektromagnetycznych.
Reinhard Kulessa
7
14.5 Prądy polaryzacyjne w dielektrykach.
Na ostatnim wykładzie stwierdziliśmy, że udział w powstawaniu
pola indukcji magnetycznej mają wszystkie możliwe prądy.
Rozważaliśmy jednak do tej pory jedynie prądy stacjonarne,
czyli niezależne od czasu. Różniczkowe prawo Ampera możemy
sformułować następująco:
Zastanówmy się co dzieje się w dielektryku przy włączaniu pola
elektrycznego.




rot B  0 ( j przew  jmol  j pol )
Włączenie pola powoduje
przesunięcie ładunku
dE/dt 0
neutralne atomy
E = const
-+ -+ -+
-+ -+ -+
-+ -+ -+
-+ -+ -+
uszeregowane dipole
Reinhard Kulessa
ładunek
powierzchniowy 
E=0
8
W chwili gdy włączamy pole w czasie dt przepływa przez jednostkę
powierzchni ładunek . Możemy więc powiedzieć, że przepływa
wtedy prąd związany z polaryzacją o natężeniu;
j pol

P
 P


 
t
t
.
Możemy więc napisać, że gęstość prądu polaryzacyjnego wynosi:


P
j pol 
t
Wektor polaryzacji związany jest z wektorem natężenia pola
elektrycznego zależnością (8.5) , czyli


P   0 ( 1) E
Reinhard Kulessa
(8.5)
9
Wprowadzając tą zależność do naszych rozważań, otrzymujemy
równanie;


j pol

E E próż .
  0

t
t
W próżni prawa część równania powinna zniknąć. Doświadczenie
pokazuje, że również w próżni istnieje człon E t .
Różniczkowe prawo Ampera przyjmuje więc ogólnie postać:




E
rot B  0 ( j przew  jmol   0 )
t
(14.21)
Powyższe równanie jest równocześnie I prawem Maxwella.
Reinhard Kulessa
10
15. Magnetyczne własności materii
15.1 Momenty magnetyczne atomów i cząsteczek
W równaniu (14.16) podaliśmy definicję orbitalnego momentu
magnetycznego.
Moment pędu (rysunek obok) jest
z L
z
wielkością skwantowaną.

2
Lz  me r   m 
m  0,1,2,....
r
e
 = 1.0546 ·10-34 Js
Orbitalny moment magnetyczny jest równy:
p
l
Mz
e

m
2me
Reinhard Kulessa
11
Do tego dochodzi własny-spinowy moment magnetyczny;
pMs z   B
W atomach wielo elektronowych momenty orbitalny i spinowy
dodają się do wypadkowego momentu magnetycznego pM.
Wartość tego momentu definiuje własności magnetyczne
materiału.
Gdy pM ≠ 0 ----- materiał jest paramagnetykiem,
Gdy pM = 0 ----- materiał jest diamagnetykiem.
Przyłożenie do jakiegoś materiału zewnętrznego pola indukcji
magnetycznej B, powoduje polaryzację dipoli magnetycznych
występujących w tym materiale. Pojawia się wtedy wielkość,
którą nazywamy magnetyzacją M.
 magn. mom. dip.
M 
jedn. obj.
Reinhard Kulessa
12
15.2 Zależność pomiędzy magnetyzacją M a prądem
cząsteczkowym jmol.
Załóżmy, że mamy jednorodnie namagnesowany cylinder.
Cały cylinder posiada magnetyczny
M
A
moment dipolowy pM = M · l · A.
Magnetyzacja ma miejsce dlatego, że
atomowe momenty dipolowe są
l
ustawione równolegle do osi cylindra.
Wewnątrz cylindra prądy atomowe
kompensują się.
I
Na powierzchni powstaje nie
skompensowana składowa prądu
powierzchniowego I.
Reinhard Kulessa
13
Jeśli podzielimy cylinder na dyski o wysokości l, to opływa
go prąd I· l/l, dając moment magnetyczny;

l 
pM  I
A
pM
A
l
l
I ·l/l
Magnetyzacja tej płytki wynosi;
| p M |
I
M 
A  l
l
(15.2)
Znaleźliśmy więc związek pomiędzy prądami molekularnymi a
magnetyzacją. Przyczyniają się do niej składowe powierzchniowe
tych prądów. Można pokazać , że ogólna postać zależności
pomiędzy prądami molekularnymi a magnetyzacją, ważna
również dla niejednorodnej magnetyzacji ma postać:


jmol  rot M
Reinhard Kulessa
(15.3)
14
M
A
Prawdziwość równania (15.3) możemy
wykazać następująco. Dla równania (15.3)
możemy definiując powierzchnię A = s·l napisać:

 

 jmol  dA   rot M  dA
A
l
I
M
A
Lewa całka w tym równaniu jest = 0 dla powierzchni
A1 , lecz jest równa I dla powierzchni A2 .
Prawa całka jest zgodnie z twierdzeniem Stokes’a
równa:
 
 
 rot M  dA   M  ds
A
s

Mamy wtedy:
l
A1
1
A2
2
 
 M  ds  M  l  M  l  0
1
 
 M  ds  M  l  0  l  I
I=I
cbdo.
2
Reinhard Kulessa
15
15.3 Wektor natężenie polamagnetycznego H.
Jeśli wprowadzimy znalezioną postać wektora gęstości prądu
molekularnego jmol do I równania Maxwella, to otrzymamy:




D
rot B   0 j przew   0
  0 rot M
t
Równanie to możemy zapisać również jako:


 B  
D
rot   M   j przew 
t
 0

(15.4)
Natężeniem pola magnetycznego H nazywamy wyrażenie:
Jednostką natężenia pola
magnetycznego jest [A/m].

H 

B
0

M
Reinhard Kulessa
(15.5)
16
15.4 Zdolność magnetyzacji materii
Zgodnie z równaniem (15.5) możemy wyrazić wektor indukcji
magnetycznej przez wetor natężenia pola magnetycznego.
Otrzymamy zależność
 


B( H )  0 ( H  M )
Równanie to zawiera w sobie skomplikowane bardzo często
własności materii.
A). paramagnetyki
Pamiętamy związek pomiędzy indukcją magnetyczną B a
natężeniem pola magnetycznego H analogiczny do związku
między D a E w elektrostatyce. Ma on postać:


B  o  H
Reinhard Kulessa
17
0 jest przenikalnością magnetyczną próżni, a  jest względną
przenikalnością magnetyczną ośrodka.
Z ostatnich dwóch równań możemy znaleźć zależność między
magnetyzacją a natężeniem pola magnetycznego.

 
0  H  0 ( H  M )


M  (   1) H


M H
Współczynnik  = ( - 1) jest podatnością magnetyczną
Dla paramagnetyków podatność magnetyczna  > 1
Jeśli posiadamy substancję paramagnetyczną, która posiada n
atomów na jednostkę objętości, a każdy atom ma dipolowy moment
magnetyczny równy m to magnetyzacja tej substancji wynosi;
Reinhard Kulessa
18


mB n m 2  ,
M  nm

B
3kT 3kT
(15.6)
Gdzie wyrażenie mB/3kT oznacza ułamek dipoli magnetycznych
ustawionych równolegle do pola indukcji B.
Stosunek
0  M

(15.7)
B
nazywamy podatnością magnetyczną substancji.
W oparciu o równania (15.6) i (15.5) możemy napisać:
n  m2
  0
3kT
Reinhard Kulessa
(15.8)
19
Należy również zauważyć, że podatność magnetyczna dla
paramagnetyków zmienia się z temperaturą zgodnie z prawem
Curie.
Dla paramagnetyków   10-9 – 10-3, a   1.
B
M
H
H
b). diamagnetyki
W diamagnetykach magnetyczne momenty orbitalne i spinowe
kompensują się. Zewnętrzne pole indukcji magnetycznej indukuje
prądy kołowe o kierunku takim, że dipolowe momenty
magnetyczne tych prądów są antyrównoległe do zewnętrznego
pola.
Reinhard Kulessa
20
Podatność magnetyczna  jest dla diamagnetyków ujemna i
niezależna od temperatury.
M
H
C). ferromagnetyki
Dla ferromagnetyków >> 1∼104, >>0. Zależność B(H)
pokazuje zjawisko histerezy.
Reinhard Kulessa
21
B(M)
BR
H
HK
Krzywą histerezy
charakteryzują dwie
wielkości, remanencja BR,
oraz koercja HK.
Ferromagnetyzm znika
powyżej temperatury Curie.
Temperatury Curie wynoszą
przykładowo dla Gd-200 C,
Dla Ni-3580 C, dla Fe-7700 C,
Co- 11310 C.
B
TC T
Reinhard Kulessa
22