Pole nieskończonej naładowanej warstwy

Wykład 9
7. Pojemność elektryczna
7.1 Pole nieskończonej naładowanej warstwy
-ładunek
powierzchniowy
z
+
S2
E2
E1
dS2
S1
y
dS1
x
18 marca 2003
Reinhard Kulessa
1
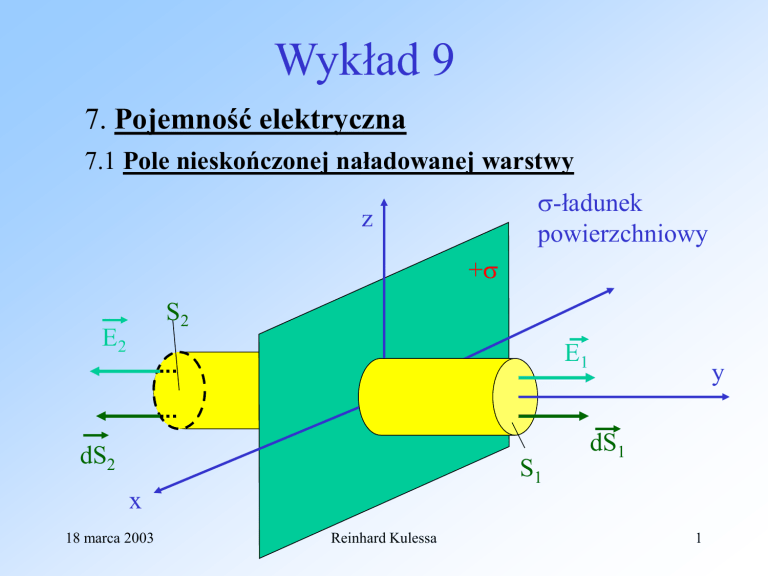
Natężenie pola elektrycznego pochodzące od nieskończonej
naładowanej warstwy możemy wyznaczyć dwoma sposobami,
metodą superpozycji, oraz w oparciu o prawo Gaussa.
Zgodnie z prawem Gaussa całkowity strumień jest równy
 
Q
0
Linie natężenia pola elektrycznego są prostopadłe do naładowanej
płaszczyzny, wobec tego całkowity strumień wynosi:
 
S




( E1  dS1  E2  dS 2 )
Widzimy z rysunku, że




dS1  dS 2 , E1   E2
Całkowity strumień jest więc równy:
18 marca 2003
Reinhard Kulessa
2
 S
  2E  S  
0
0
Q
Czyli:


E 
2 0
Pole pochodzące od tej warstwy wygląda następująco:
z
 
E
yˆ 0
2 0


E
yˆ 0
2 0
y
18 marca 2003
Reinhard Kulessa
3
7.2 Pole między dwoma nałądowanymi warstwami + i -
Zastanówmy się jaka jest wartość pola pomiędzy dwoma
przeciwnie naładowanymi warstwami.
-
+

2 0

2 0
y

2 0
18 marca 2003

2 0
Reinhard Kulessa
4
7.3 Kondensator płaski
Zajmijmy się układem dwóch płasko-równoległych
przewodników (elektrod) o powierzchni S położonych w
odległości d od siebie. Elektrody są naładowane odpowiednio
ładunkami +Q i –Q.
Układ taki nazywamy kondensatorem płaskim.
S
Gęstość
powierzchniowa
+Q
Ê
ładunku wynosi:
 = Q/S
d
-Q
Pole wewnątrz elektrod z pominięciem efektów brzegowych jest
jednorodne.
Niech różnica potencjałów pomiędzy elektrodami wynosi V.
18 marca 2003
Reinhard Kulessa
5
Oznaczmy tą różnicę przez V  V1(  )  V2(  )
.
Z zależności pomiędzy potencjałem a natężeniem pola
elektrycznego r. (5.9) otrzymujemy, że:
V1(  )  V2(  ) V
E

d
d
Widzimy więc, że:
V  E  d , a korzystając z obliczonej
poprzednio wartości natężenia pola elektrycznego pomiędzy
dwoma naładowanymi płaszczyznami otrzymujemy:
Qd
V 
0  S
18 marca 2003
Reinhard Kulessa
(7.1)
6
Wprowadźmy pojęcie pojemności kondensatora jako
współczynnika we wzorze:
Q  C V
(7.2)
Pojemność kondensatora płaskiego wynosi więc:
C
18 marca 2003
0  S
(7.3)
d
Reinhard Kulessa
7
7.4 Kondensator kulisty
Rozpatrzmy układ dwóch współśrodkowych czasz kulistych
naładowanych odpowiednio ładunkami +Q i –Q.
E
+Q
r1
r2
-Q
R
dS
Pole elektryczne dla takiego
układu jest polem radialnym,
 
więc
E  E (r )
Policzmy strumień pola
elektrycznego przechodzącego
przez powierzchnię kuli w
środku „0” i promieniu R
r1  R  r2
.

 
2
E

d
S

E
d
S

4

R
E


18 marca 2003
Reinhard Kulessa
8
Z prawa Gaussa otrzymamy:
4R E 
2
Q
0
Q
 E 
40 R 2
dla dowolnego R z podanego poprzednio przedziału.
Różnica potencjałów V=V1 – V2 wartość:
r2
Q
r1
40
V    E r  dr  

r2
r1
dr

2
r
r2
Q  1
Q r2  r1

  
40  r  r1 40 r1  r2
Zgodnie z wzorem (7.2) otrzymujemy na pojemność kondensatora
złożonego z dwóch czasz kulistych wyrażenie:
18 marca 2003
Reinhard Kulessa
9
r1  r2
C  40
r2  r1
(7.4)
Z wyrażenia tego widać, że gdy r2   pojemność
kondensatora kulistego, inaczej mówiąc pojemność
przewodnika będącego kulą jest równa:
C  40  r1
Jednostką pojemności w układzie SI jest FARAD.

1C
1F 
 1m 2 kg 1 s 4 A2
1V

Pojemność kuli ziemskiej, R~6.4 106 m, C = 710 F, a kula o
pojemności 1F ma promień 9 106 km.
18 marca 2003
Reinhard Kulessa
10
7.5 Kondensator cylindryczny.
Kondensator cylindryczny składa się z dwóch współśrodkowych
cylindrów o p promieniach a i b.
Stosując Prawa Gaussa
dla dowolnej odległości
r od środka walców
otrzymujemy, że
b
a
l
E  2rl 
Pow.
-Q
+Q
Q
0
r
Na wartość potencjału otrzymamy więc wyrażenie:
18 marca 2003
Reinhard Kulessa
11
a
a
V    Edr   
b
b
Q
20 rl
dr 
a
1
Q
ln a  ln b  

dr  

20l b r
20l
Q
b
ln b  ln a  

ln  
20l
20l  a 
Q
Q
Pojemność kondensatora cylindrycznego wynosi
więc:
Q 20l
C 
V
b
ln  
a
18 marca 2003
Reinhard Kulessa
(7.5)
12
7.6 Łączenie kondensatorów
7.6.1 Połączenie równoległe
V1
+Q1
+Q2
C1
V2
-Q1
+Q3
+Q4
C2
C3
-Q2
C4
-Q3
-Q4
Potencjał V = V1 – V2 jest taki sam na każdym
kondensatorze.
Ładunek, który znajduje się na każdym z kondensatorów
Qi  Ci  V
, a całkowity ładunek Q 
Otrzymujemy więc
i
i
.
Q  iCi  V  V  iCi . Czyli
C
18 marca 2003
Q
C
i
i
Reinhard Kulessa
(7.5)
13
7.5.2 Połączenie szeregowe
C1
+Q
V
C2
-Q
+Q
V1
C3
-Q +Q
V2
C4
-Q
V3
+Q
-Q
V4
Ładunki na okładkach kondensatorów połączonych szeregowo są
jednakowe. Całkowita różnica potencjałów jest równa sumie
różnic potencjałów między okładkami poszczególnych
kondensatorów V 
Vi .

i
Wiemy, że
18 marca 2003
Vi  Q
Ci
czyli
Reinhard Kulessa
V  Q  11 / Ci
.
14
Otrzymujemy więc
1

C
18 marca 2003
1

i Ci
Reinhard Kulessa
(7.6)
15
7.6 Ziemia jako kondensator kulisty
Mimo, że wydaje się nam, że Ziemia jest ładunkowo obojętna, to
doświadczenie uczy, że tak nie jest. Na Ziemi zachodzi szereg
zjawisk charakterystycznych dla ciał naładowanych. Znane nam są
wszystkim wyładowania atmosferyczne w czasie burz, ale jak jest
w czasie gdy nie ma burz.
Okazuje się, że w atmosferze istnieje pionowe pole elektryczne o
natężeniu E ~ 100V/m. Co 1 m wysokości potencjał wzrasta o
100 V. Ładunek Ziemi jest ujemny.
Warunkiem istnienia pola jest:
1. Obecność jonów w atmosferze,
2. Rozdzielenie istniejących ładunków przez jakiś mechanizm.
Ad. 1. Przypuszczano, że obecność jonów w atmosferze
związana jest z naturalna promieniotwórczością. Wtedy liczba
18 marca 2003
Reinhard Kulessa
16
jonów powinna być największa przy powierzchni Ziemi.
Stwierdzono jednak, że liczba jonów rośnie z wysokością i
osiąga maksimum na wysokości powyżej 50 km, na wysokości
gdzie rozciąga się tzw. jonosfera.
Jonizacja jest wywoływana przez promieniowanie kosmiczne.
Ad 2. Ziemia ma ładunek ujemny a potencjał powietrza jest
dodatni.
Stale więc płynie
+ + + + + + + + + + 50 km
prąd ładunków
dodatnich z
Prąd
atmosfery do Ziemi.
400000 V
10-2 jonu/(s m2)
Całkowity prąd ma
moc ok. 700 MW
18 marca 2003
Reinhard Kulessa
17
Taki prąd powinien w ciągu 0.5 godz. wyrównać różnicę
ładunków.
Aby dać odpowiedź na pytanie jaki mechanizm dostarcza
ujemnych ładunków powierzchni Ziemi wykonano w różnych
miejscach pomiarów zmiany potencjałów i prądów. Wybierano
zwykle pogodne dni nad oceanami. Pogodne dni wybierano aby
uniknąć wpływu burz na pomiary, a oceany miały osłabić
procesy jonizacji zwykle silniejsze nad kontynentami. W wyniku
tych pomiarów stwierdzono że:
średni gradient potencjału zmienia się o ±15% wraz ze
zmianą czasu uniwersalnego.
V/cm
100
90
6
18 marca 2003
12
18
Reinhard Kulessa
24
Godz.(Greenwich)
18
Świadczy to o tym, że:
a) Na dużych wysokościach istnieje duże przewodnictwo
poziome, wobec tego różnica potencjałów między
jonosferą a Ziemią nie zmienia się.
b) Istnieje mechanizm ładowania Ziemi ładunkiem ujemnym
ze średnim prądem 1800 A.
Odpowiedzialne za to są burze, głównie tropikalne, a
rozładowanie następuje w okresie ładnej pogody.
(Patrz Feynmann t.II cz.I § 9-4 na temat mechanizmów
powstawania burz na Ziemi)
18 marca 2003
Reinhard Kulessa
19
8. Materia w polu elektrycznym
Na każdy ładunek umieszczonej w polu elektrycznym materii
działa siła wynikająca z prawa Coulomba. Ze względu na różną
ruchliwość ładunków w różnych materiałach można
zaobserwować następujące zjawiska:
a). W przewodniku ruchliwe elektrony zostają przesunięte
w stosunku do dodatnich atomów, co daje rozdzielenie
ładunków dodatnich od ujemnych, czyli tzw. zjawisko
indukcji.
b). W izolatorach nośniki ładunku zostają przesunięte tylko
nieznacznie, obserwujemy tzw. polaryzację.
Rozważmy przewodnik umieszczony w polu elektrycznym.
Znajdujące się w nim swobodne elektrony będą przesuwały
się w określonym kierunku.
18 marca 2003
Reinhard Kulessa
20
-
----- -- -- -- --
-
- - Eˆ-Cond .
-
+
+
+
+
+
+
+
Ê
Doprowadzi to do nagromadzenia się na ściankach przewodnika
tzw. ładunku indukcyjnego. Ładunek ten generuje wewnątrz
przewodnika pole elektryczne skierowane przeciwnie do pola
zewnętrznego.
Przesuwanie się ładunku trwa tak długo, aż wypadkowe pole
wewnątrz przewodnika osiągnie wartość zero.
18 marca 2003
Reinhard Kulessa
21
-
----- ˆ
- - ECond .
----
+
+
+
+
+
+
+
Ê
ładunki indukcyjne
Zastanówmy się teraz jak wygląda sytuacja, gdy w polu
elektrycznym umieścimy materiał nie przewodzący ładunku.
Doświadczenie uczy nas, że jeśli pomiędzy dwa ładunki
wprowadzimy izolator, to maleje siła kolumbowska
działająca pomiędzy ładunkami.
18 marca 2003
Reinhard Kulessa
22
Omówmy ten problem na przykładzie kondensatora płaskiego.
C2
C1
powietrze
dielektryk
Po włożeniu dielektryka pomiędzy okładki kondensatora płaskiego,
na pewno nie zmienił się ładunek na okładkach a jednak zmalał
potencjał jak wskazał elektroskop. Zgodnie ze wzorem (7.2)
musiała wzrosnąć pojemność kondensatora. Równocześnie spadek
potencjału na okładkach oznacza spadek natężenie pola
elektrycznego wewnątrz okładek. (cdn)
18 marca 2003
Reinhard Kulessa
23