Wykład 4
5.3 Prawo Gaussa w postaci różniczkowej
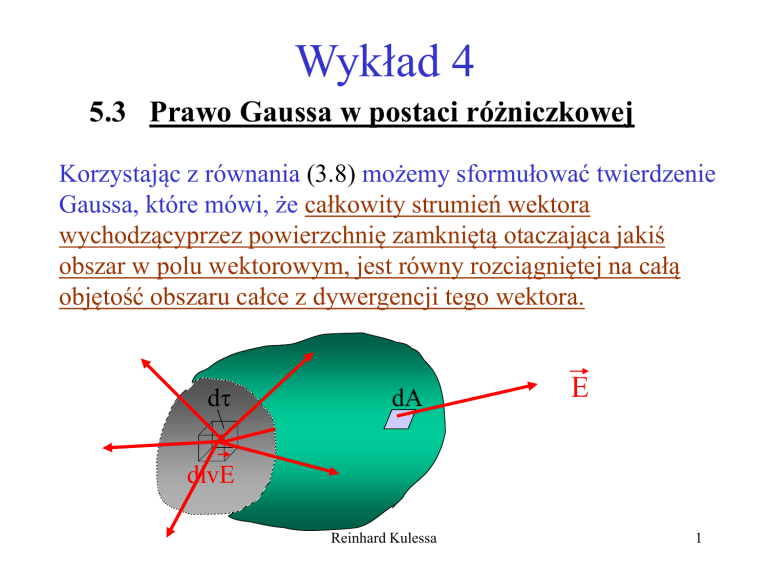
Korzystając z równania (3.8) możemy sformułować twierdzenie
Gaussa, które mówi, że całkowity strumień wektora
wychodzącyprzez powierzchnię zamkniętą otaczająca jakiś
obszar w polu wektorowym, jest równy rozciągniętej na całą
objętość obszaru całce z dywergencji tego wektora.
d
dA
E
divE
Reinhard Kulessa
1
E dA divE d
A
(5.6)
Jeśli porównamy równania (5.5) i (5.6) to otrzymamy
różniczkową postać prawa Gaussa.
div E 4 k ( x, y , z )
0
(5.7)
Ładunki elektryczne możemy więc nazwać źródłami pola
elektrycznego. Gdy nie ma wypływającego z objętości
strumienia, nie ma źródeł. Pole v, dla którego div v = 0 jest
polem bezźródłowym.
Reinhard Kulessa
2
5.4 Twierdzenie Stokes’a
Analogicznie do związku pomiędzy dywergencją a
przestrzenną gęstością strumienia pola wektorowego, istnie
je związek pomiędzy składowymi rotacji a
powierzchniowymi gęstościami odpowiednich cyrkulacji.
ds
ds
dA
A
v
vt
Wektor n jest wektorem
prostopadłym do elementu
powierzchni dA.
ds
Wobec tego wektor
v
dA = dA n
n
rot v
Reinhard Kulessa
Powierzchnia A jest
naciągnięta na pętlę
3
Określa to twierdzenie Stokes’a
v
d
s
rot
v
d
A
Pole wektorowe
(5.8)
A
v
może być polem sił F.
Wiemy, że pole wektorowe jest polem bezwirowym, jeśli
rotacja tego pola jest równa zero. Dla bezwirowego pola sił
(rot F = 0) wynika, że praca siły F po zamkniętym obwodzie
jest równa zero.
Takie pole sił nazywamy polem zachowawczym.
Reinhard Kulessa
4
O polu elektrycznym wiemy, że jest polem centralnym. Dla pola
centralnego cyrkulacja wektora pola jest równa zero, czyli
v ds
A
rot v dA 0
Natężenie pola elektrycznego ładunku punktowego spełnia tą
zależność:
r0
Q
E ds 40 r 2 ds 0
Weźmy rozkład linii sił natężenia pola pochodzących od
ładunku punktowego.
Reinhard Kulessa
5
ds
r0
E
Krążenie natężenia pola
elektrycznego liczymy po
zielonym konturze
.
Na łukach r0 ds
Na promieniach przyczynki się
nawzajem znoszą.
Wynika stąd, że
A
rot E dA 0 .
Czyli,
rot E 0 .
Pole elektrostatyczne jest więc polem bezwirowym.
Reinhard Kulessa
6
Z bezwirowości pola elektrostatycznego wynika istnienie
potencjału skalarnego V(r) takiego, że;
E grad V (r )
(5.9)
5.5 Potencjał skalarny pola elektrycznego.
Do wyrażenia na natężenie pola elektrycznego postaci (5.9)
możemy dojść w oparciu o wzór (5.3).
1
( ) d
E (r )
(r )
3
40 r
Reinhard Kulessa
(5.3)
7
Występujący w tym wzorze element objętości d możemy
zapisać jako d = d3.
Zauważmy, że dla funkcji występującej pod całką występuje
następująca zależność:
(r )
1
grad
3
r
r
.
Wiedząc, że składowe gradientu są następujące:
grad ( , , )
x y z
Reinhard Kulessa
8
oraz
1
1
( x 1 ) 2 ( y 2 ) 2 ( z 3 ) 2
r
,
1 2( x 1 )
3
x r
2
r
otrzymamy:
1
1
1 2( y 1 )
3
y r
2
r
1
1 2( z 1 )
3
z r
2
r
Reinhard Kulessa
9
W oparciu o podane wyrażenia możemy wzór na natężenie pola
elektrycznego pochodzącego od objętościowego rozkładu
ładunków (5.3) napisać następująco:
1
E ( r ) grad (
40
( ) d
)
r
.
Funkcję skalarną
V (r )
( ) d
40
r
1
(5.10)
Nazywamy skalarnym potencjałem pola elektrycznego.
Reinhard Kulessa
10
Analogiczne wyrażenia na potencjał pola dla układu ładunków
powierzchniowych, punktowych i dla ładunku pojedynczego
możemy wyprowadzić odpowiednio w oparciu o równania
(5.3a), (5.2) i (5.1).
Dla pojedynczego ładunku w oparciu o wzór (5.1) mamy:
E
Wiadomo, że
Q r
40 r 3
dV r
E grad V ( r )
dr r
Reinhard Kulessa
,
11
Czyli
dV
Q
40 r
2
dr
. .
Po wycałkowaniu otrzymujemy :
V (r)
Q
40 r
C
Przyjmujemy, że w nieskończoności (r =) potencjał pochodzący
od ładunku Q jest równy zero. Musimy wtedy przyjąć, że stała C
jest równa zero.
Reinhard Kulessa
12
Ten sam wynik otrzymamy, jeśli wprowadzimy odpowiednie
granice całkowania
r
V (r)
Q
40 r
2
dr
Q
40 r
(5.11)
Można łatwo pokazać, że wyrażenie pod całką jest równe E dr ,
czyli
V ( r ) E dr
r
(5.11a)
Potencjał określony we wzorze (5.11) jest równy pracy potrzebnej
do przeniesienia ładunku jednostkowego q=1C z nieskończoności
na odległość r od ładunku Q.
Reinhard Kulessa
13
W oparciu o definicję potencjału (5.11a) możemy zdefiniować
różnicę potencjału UAB pomiędzy dwoma punktami pola
elektrostatycznego.
VrA VrB E ( r ) dr
rA
U AB
(5.11b)
rB
Ze względu na to, że pole elektryczne jest polem centralnym i ma
charakter zachowawczy (r. (5.9) ), tak samo jak w mechanice,
praca potrzebna na przesunięcie ładunku w polu jest niezależna od
drogi po której ją wykonujemy.
2
2
F ds q E ds q grad V ds
2
W1,2
1
1
Reinhard Kulessa
1
14
Praca potrzebna do przesunięcia ładunków Q z A do B w
polu elektrycznym jest taka sama niezależna od drogi.
A
B
Q1
Q2
Q1
Q3
Q2
Q3
Reinhard Kulessa
Ê
15
Q
Ê
Praca wykonana na przesunięcie ładunku po drodze zamkniętej jest
równa zero
F dl 0
Reinhard Kulessa
16
Ponieważ grad V ds dV
ds
1
2
Możemy w oparciu o ostatnie
równanie napisać;
W1,2 q (V1 V2 )
(5.12)
Dla układu N ładunków punktowych otrzymamy na potencjał w
punkcie r wyrażenie:
N
Q
1
V (r )
1 40 r
Reinhard Kulessa
(5.13)
17
5.5 Równanie Poissona i Laplace’a
Pamiętamy podane w równaniu (5.7) różniczkowe prawo
Gaussa.
(r )
div E
0
Jeśli do tego równania podstawimy wartość natężenia pola
elektrycznego E(r) wyrażone przez potencjał pola V(r)
zgodnie ze wzorem (5.9), otrzymamy następujące równanie:
div grad V ( r )
(r )
0
(5.14)
zwane równaniem Poissona.
Reinhard Kulessa
18
Ostatnie równanie możemy napisać w postaci operatorowej.
2
div grad V ( r ) (V ) V ( )V V
Z drugiej strony
V V V
V
x x y y z z
V V V
2 2
2
x
y
z
2
2
Reinhard Kulessa
2
19
Operator 2 nosi nazwę laplasjanu.
2 2 2
x
y
z
2
2
2
2
Bardzo często stosuje się zapis
2
(5.15)
.
W przypadku pola bezźródłowego równanie Poissona przechodzi
w równania Laplace’a.
V 0
2
Reinhard Kulessa
(5.16)
20
Równanie Poissona i Laplace’a, oraz prawo Gaussa, są trzema
podstawowymi równaniami pola elektrycznego E. Wynikają one
Bezpośrednio z prawa Coulomba. Wprowadzenie strumienia
pola elektrycznego było praktyczne i poglądowe, lecz można
się było bez tego obyć.
Reinhard Kulessa
21
5.6 Podsumowanie wiadomości o polu elektrycznym
Na poprzednich wykładach poznaliśmy następujące informacje
dotyczące pola elektrycznego:
1. Cyrkulacja pola
2. Rotacja pola , definicja pola bezwirowego, pola o
zerowej rotacji
3. Twierdzenie Stokes’a, podjące związek pomiędzy całką
po konturze, a całką powierzchniową,
4. Definicja gradientu pola,
5. Istnienie dla pola elektrycznego, które jest bezwirowe
potencjału skalarnego, którego gradient jest równy
natężeniu pola elektrycznego.
Reinhard Kulessa
22
6. Dywergencję funkcji wektorowej,
7. Prawo Gaussa, również w postaci różniczkowej
8. Twierdzenie Gaussa podające związek pomiędzy całką
powierzchniową a objętościową ,
9. Definicja potencjału skalarnego pola ,
10. Równania Poissona i Laplace’a pozwalające wyliczyć
potencjał pola,
Rozważmy pole elektryczne, dla którego gęstość ładunku
=0. Wtedy dla potencjału spełnione jest równanie Poissona
z =0, czyli równanie Laplace’a, V=0 . Jednoznaczne
znalezienie potencjału wymaga dodatkowo podania
warunków brzegowych, inaczej zawsze można by podać
rozwiązanie V0.
Reinhard Kulessa
23