Weźmy rozkład linii sił natężenia pola pochodzących od ładunku

Wykład 2
4.1 Prawo Coulomba
W 1785 roku w oparciu o doświadczenia z ładunkami
Charles Augustin Coulomb doszedł do trzech
następujących
wniosków dotyczących siły F działającej pomiędzy dwoma
ładunkami Q1 i Q2;
•
•
•
F  Q1 • Q 2
F  1/r2
F jest przyciągająca dla ładunków przeciwnych (+/-)
a odpychająca dla jednakowych (+/+), (-/-) i działa wzdłuż
linii łączącej ładunki.
W doświadczeniach swoich Coulomb posługiwał się tzw. Wagą
Skręceń
Reinhard Kulessa
1
Waga Skręceń
+
-
+
Równowaga następowała wtedy, gdy moment sił
sprężystości nici był równy momentowi związanemu z
oddziaływaniem ładunków.
Prawo swoje Coulomb sformułował następująco:

Q1  Q2
F k
r2
Reinhard Kulessa

r
r
(4.1)
2

r
Wektor
jest wektorem położonym na linii łączącej
dwa oddziałujące ładunki.
Ze znajomości wielkości siły i odległości pomiędzy ładunkami
możemy przez definicję stałej k zdefiniować wielkość ładunku.
W układzie SI
k
1
40
7
 10 c
2
Gdzie c jest prędkością światła w próżni:
0
c = 299792458 m/s
jest przenikalnością elektryczną próżni i jest równe:
 0  8.85  10 12 C 2 /( N  m 2 )
k  8.9875  109 N  m 2 / C 2
Reinhard Kulessa
3
Jednostką ładunku w układzie SI jest KULOMB.
Ciało posiada ładunek jednego kulomba jeśli na równy
sobie działa z odległości jednego metra siłą 9. 109 Newtona.
Prawo Kulomba jest spełnione w fizyce makroskopowej i
atomowej z dokładnością jak 1 do 109.
Jeśli umieścimy dwa ciała o masach po 1 kilogramie i ładunku
jednego kulomba w odległości 1m od siebie, to stosunek siły
kulombowskiej do siły grawitacji ma się jak 1019: 1.
1C
1m
1 kg
1C
1 kg
Reinhard Kulessa
Fkul
 1019
Fgraw
4
5 Pole elektryczne
5.1 Natężenie pola elektrycznego
Z prawa Coulomba wiemy, że ładunki oddziałują pomiędzy
sobą siłą zależną od wielkości tych ładunków i ich odległości.
Możemy więc powiedzieć, że wokół każdego ładunku
roztacza się pewien obszar, POLE, w którym na inne ładunki
działają siły kulombowskie.
Pole wytworzone przez ładunki elektryczne nazywamy
polem elektrycznym.
Pole takie charakteryzuje się natężeniem informującym nas
o wielkości siły działającej na ładunek umieszczony w tym
polu.
Reinhard Kulessa
5
Natężenie pola elektrycznego definiujemy jako stosunek siły
działającej na ładunek próbny q0 umieszczony w polu, do
wielkości tego ładunku.
z
E
r
q0
F
y
Q
x
 
E ( r )  lim
q0 0
Reinhard Kulessa


F
Q

r
3
q0
40 r
(5.1)
6
We wzorze (5.1) granicę dla q0  0 wprowadzamy dlatego,
aby otrzymać wartość natężenia pola elektrycznego
pochodzącego tylko od ładunku Q .
Fakt, że natężenie pola
elektrycznego
jest proporcjonalne
do wielkości ładunku, leży
u podstawy
zasady superpozycji.
Zasada ta mówi, że
natężenie pola
elektrycznego
w danym punkcie jest sumą
pól pochodzących od
poszczególnych ładunków.
z
Q1
Q2
Q3
Px
Q4
r
i
Qi
y
x
Reinhard Kulessa
7
Dla układu ładunków punktowych otrzymujemy zgodnie z
zasadą superpozycji następujące wyrażenie na natężenie
pola elektrycznego:
 
E (r ) 
1
40
i

1
Qi


r  i


(r  i )
3
(5.2)
Ładunek może być rozłożony nie tylko punktowo, ale
również objętościowo lub powierzchniowo. Jeśli
zdefiniujemy gęstość ładunku jako (x,y,z) [C/cm3], to
ładunek zawarty w elemencie objętości d jest równy:
dQ =  d.
Reinhard Kulessa
8
P
z

x
r
d

y
x
Obłok ładunku
Natężenie pola w punkcie pochodzącego od
ładunku rozmieszczonego w objętości 
dane jest wzorem:
 
1
E (r ) 
40


 ( )  d  
(r   )

3

r 
Reinhard Kulessa
(5.3)
9
Analogiczny wzór możemy napisać dla ładunku rozłożonego
na powierzchni A z gęstością powierzchniową (x,y,z).
z
Px
r
dA

y
x

 
1
 ( )  dA  
E (r ) 
 (r   )


3
40 A r  
Reinhard Kulessa
A
Natężenie pola w punkcie P
pochodzącego od ładunku
rozmieszczonego na
powierzchni A dane jest
wzorem:
(5.3a)
10
5.2 Prawo Gaussa
We wzorze (3.1) podaliśmy definicję strumienia dowolnego
wektora pola. W ten sam sposób możemy zdefiniować
strumień natężenia pola elektrycznego.
Prawo Gaussa mówi nam, że:
Strumień natężenia pola elektrycznego E przez dowolną
powierzchnię, równa się sumie całkowitego ładunku
zamkniętego w tej powierzchni, razy stała k.
A)
dA
Q
E
r0
Reinhard Kulessa
11
Otrzymujemy:

 

 E   E  dA   E  dA 
A
A

2
 E  4r0 
(5.5)
Q
2
 k 2  4r0  k 4Q
r0
W układzie SI otrzymujemy na wartość strumienia w
omawianym
1
Q
przypadku wartość ( k 
):
E 
40
0
Reinhard Kulessa
12
B). Tą samą wartość strumienia natężenia pola elektrycznego
otrzymujemy, otaczając ładunek dowolną powierzchnią A.
dA``
dA`
dA0
E
E0
dA
Q+
r0
A
    '   ''
'
d  E  dA  E  dA  E  dA  E  dA
Reinhard Kulessa
13
Ponieważ E1/r2, stąd wynika, że E=E0(r0/r)2. Z drugiej strony
dA’/dA0=(r/r0)2. Wynika z tego, że d= E dA’= E0 dA0.
Otrzymujemy więc na strumień natężenia pola
elektrycznego taki sam rezultat jak w punkcie A).


A
E  dA 

sfera
E0  dA0  4 kQ 
Q
0
(5.4a)
C). Wiele ładunków zamkniętych powierzchnią.
A
A’
Reinhard Kulessa
14
N
 
 '
1 N
   E  dA   ' E  dA  4k  Q   Q
a
 0  1
 1
A
(5.4b)
N
Gdzie  Q  Q jest całkowitym ładunkiem.
 1
D). Ładunki Q znajdujące się poza zamkniętą
powierzchnią
Zgodnie z C) =0. Przez
powierzchnię wychodzi
tyle samo linii pola, co
wchodzi.
A
Reinhard Kulessa
15
Jeśli mamy do czynienia z objętościowym rozkładem ładunku
(x,y,z), wtedy przyjmując, że (x,y,z)=dQ/d, równanie (4.5b)
przyjmie postać:
 
1
   E  dA 
A
0
  ( x, y, z )
d
(5.5)
Pamiętamy, że A jest całkowitym polem powierzchni otaczającej
ładunek, a  całkowitą objętością zajmowaną przez ładunek.
Podsumowanie: Strumień natężenia pola elektrycznego przez
dowolną powierzchnię, obejmujący dowolny
rozkład ładunku, jest niezależny od kształtu tej powierzchni i
zależy jedynie od wielkości ładunku położonego wewnątrz
powierzchni.
Reinhard Kulessa
16
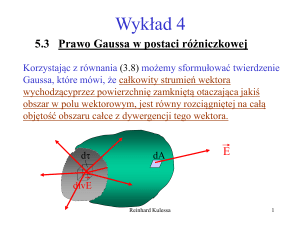
5.3 Prawo Gaussa w postaci różniczkowej
Korzystając z równania (3.8) możemy sformułować
twierdzenie Gaussa, które mówi, że całkowity strumień
wektora wychodzący przez powierzchnię zamkniętą
otaczająca jakiś obszar w polu wektorowym, jest równy
rozciągniętej na całą objętość obszaru całce z dywergencji
tego wektora.
d
dA
E
divE
Reinhard Kulessa
17
 

 E  dA   divE d
A

(5.6)
Jeśli porównamy równania (5.5) i (5.6) to otrzymamy
różniczkową postać prawa Gaussa.


div E  4 k ( x, y , z ) 
0
(5.7)
Ładunki elektryczne możemy więc nazwać źródłami pola
elektrycznego. Gdy nie ma wypływającego z objętości
strumienia, nie ma źródeł. Pole v, dla którego div v = 0
nazywamy polem bezźródłowym.
Reinhard Kulessa
18
5.4 Twierdzenie Stokes’a
Analogicznie do związku pomiędzy dywergencją a
przestrzenną gęstością strumienia pola wektorowego,
istnie je związek pomiędzy składowymi rotacji a
powierzchniowymi gęstościami odpowiednich cyrkulacji.

ds


ds
dA
A

v
vt
Wektor n jest wektorem
prostopadłym do elementu
powierzchni dA.

ds
Wobec tego wektor

v
dA = dA n
n
rot v
Reinhard Kulessa
Powierzchnia A jest
naciągnięta na pętlę 
19
Określa to twierdzenie Stokes’a
 
 
v

d
s

rot
v

d
A



Pole wektorowe
(5.8)
A

v
może być polem sił F.
Wiemy, że pole wektorowe jest polem bezwirowym, jeśli
rotacja tego pola jest równa zero. Dla bezwirowego pola
sił (rot F = 0) wynika, że praca siły F po zamkniętym
obwodzie jest równa zero.
Takie pole sił nazywamy polem zachowawczym.
Reinhard Kulessa
20
O polu elektrycznym wiemy, że jest polem centralnym. Dla
pola centralnego cyrkulacja wektora pola jest równa zero,
czyli

 
 v  ds 


A

rot v  dA  0
Natężenie pola elektrycznego ładunku punktowego spełnia
tą zależność:

 
r0 
Q
E  ds  40  r 2  ds  0
Weźmy rozkład linii sił natężenia pola pochodzących od
ładunku punktowego.
Reinhard Kulessa
21

ds


r0
E
Krążenie natężenia pola
elektrycznego liczymy po
zielonym konturze

 .
Na łukach r0 ds
Na promieniach przyczynki
się nawzajem znoszą.
Wynika stąd, że

A
 
rot E  dA  0 .
Czyli,

rot E  0 .
Pole elektrostatyczne jest więc polem bezwirowym.
Reinhard Kulessa
22
Z bezwirowości pola elektrostatycznego wynika istnienie
potencjału skalarnego V(r) takiego, że;


E   grad V (r )
(5.9)
5.5 Potencjał skalarny pola elektrycznego.
Do wyrażenia na natężenie pola elektrycznego postaci (5.9)
możemy dojść w oparciu o wzór (5.3).

 
1
 ( )  d  
E (r ) 
(r   )


3
40  r  
Reinhard Kulessa
(5.3)
23
Występujący w tym wzorze element objętości d możemy
zapisać jako d = d3 = d 1 · d 2 · d 3.
Zauważmy, że dla funkcji występującej pod całką występuje
następująca zależność:
 
(r   )
1
  grad  
 3
r 
r 
.
Wiedząc, że składowe gradientu są następujące:
  
grad    ( , , )
x y z
Reinhard Kulessa
24
oraz
otrzymamy:
1
1
  
( x  1 ) 2  ( y   2 ) 2  ( z   3 ) 2
r 
,

1
1 2( x  1 )
 
3
x r  
2
r 

1
1 2( y   2 )
 
3
y r  
2
r 

1
1 2( z   3 )
 
3
z r  
2
r 
Reinhard Kulessa
25
W oparciu o podane wyrażenia możemy wzór na natężenie pola
elektrycznego pochodzącego od objętościowego rozkładu
ładunków (5.3) napisać następująco:
 
1
E ( r )   grad (
40


 ( ) d
  )
r 
.
Funkcję skalarną

V (r ) 

 ( ) d




40
r 
1
(5.10)
Nazywamy skalarnym potencjałem pola elektrycznego.
Reinhard Kulessa
26
Analogiczne wyrażenia na potencjał pola dla układu
ładunków powierzchniowych, punktowych i dla ładunku
pojedynczego możemy wyprowadzić odpowiednio w
oparciu o równania (5.3a), (5.2) i (5.1).
Dla pojedynczego ładunku w oparciu o wzór (5.1) mamy:

E
Wiadomo, że

Q r
40 r 3



dV r
E   grad V ( r )  
dr r
Reinhard Kulessa
,
27
Czyli
dV  
Q
40 r
2
dr
. .
Po wykonaniu całkowania otrzymujemy :
V (r) 
Q
40 r
C
Przyjmujemy, że w nieskończoności (r =) potencjał
pochodzący od ładunku Q jest równy zero. Musimy wtedy
przyjąć, że stała C jest równa zero.
Reinhard Kulessa
28
Ten sam wynik otrzymamy, jeśli wprowadzimy odpowiednie
granice całkowania
r
V (r)  

Q
40 r
2
dr 
Q
40 r
(5.11)
 
Można łatwo pokazać, że wyrażenie pod całką jest równe E  dr ,
czyli
 
V ( r )    E  dr
r
(5.11a)

Potencjał określony we wzorze (5.11) jest równy pracy
potrzebnej do przeniesienia ładunku jednostkowego q=1C z
nieskończoności na odległość r od ładunku Q.
Reinhard Kulessa
29
W oparciu o definicję potencjału (5.11a) możemy zdefiniować
różnicę potencjału UAB pomiędzy dwoma punktami pola
elektrostatycznego.
  
 VrA  VrB    E ( r )  dr
rA
U AB
(5.11b)
rB
Ze względu na to, że pole elektryczne jest polem centralnym i
ma charakter zachowawczy (r. (5.9) ), tak samo jak w
mechanice, praca potrzebna na przesunięcie ładunku w polu
jest niezależna od drogi po której ją wykonujemy.
2
2
 
 

  F  ds  q  E  ds  q  grad V  ds
2
W1,2
1
1
Reinhard Kulessa
1
30
Praca potrzebna do przesunięcia ładunków Q z A do B w
polu elektrycznym jest taka sama niezależna od drogi.
A
B
Q1
Q2
Q1
Q3
Q2
Q3
Reinhard Kulessa
Ê
31
Q
Ê
Praca wykonana na przesunięcie ładunku po drodze zamkniętej jest
równa zero
 F  dl  0
Reinhard Kulessa
32

Ponieważ grad V  ds  dV
ds
1
2
Możemy w oparciu o ostatnie
równanie napisać;
W1,2  q (V1  V2 )
(5.12)
Dla układu N ładunków punktowych otrzymamy na
potencjał w punkcie r wyrażenie:
N

Q
1
V (r )  


 1 40 r  
Reinhard Kulessa
(5.13)
33
5.5 Równanie Poissona i Laplace’a
Pamiętamy podane w równaniu (5.7) różniczkowe prawo
Gaussa.

  (r )
 div E 
0
Jeśli do tego równania podstawimy wartość natężenia
pola elektrycznego E(r) wyrażone przez potencjał pola
V(r) zgodnie ze wzorem (5.9), otrzymamy następujące
równanie:

 div grad V ( r ) 

 (r )
0
(5.14)
zwane równaniem Poissona.
Reinhard Kulessa
34
Ostatnie równanie możemy napisać w postaci
operatorowej.
 
 
  
2
div grad V ( r )    (V )    V  (  )V   V
Z drugiej strony
 
 V  V  V
  V 



x x y y z z
V V V
 2  2
2
x
y
z
2
2
Reinhard Kulessa
2
35
 
Operator     2 nosi nazwę laplasjanu.



  2  2  2
x
y
z
2
2
2
2
Bardzo często stosuje się zapis
 
2
(5.15)
.
W przypadku pola bezźródłowego równanie Poissona
przechodzi w równania Laplace’a.
V 0
2
Reinhard Kulessa
(5.16)
36
Równanie Poissona i Laplace’a, oraz prawo Gaussa, są trzema
podstawowymi równaniami pola elektrycznego E. Wynikają one
bezpośrednio z prawa Coulomba. Wprowadzenie strumienia
pola elektrycznego  było praktyczne i poglądowe, lecz można
się było bez tego obyć.
Reinhard Kulessa
37
5.6 Podsumowanie wiadomości o polu elektrycznym
Na poprzednich wykładach poznaliśmy następujące
informacje dotyczące pola elektrycznego:
1. Cyrkulacja pola
2. Rotacja pola , definicja pola bezwirowego, pola o
zerowej rotacji
3. Twierdzenie Stokes’a, podjące związek pomiędzy
całką
po konturze, a całką powierzchniową,
4. Definicja gradientu pola,
5. Istnienie dla pola elektrycznego, które jest bezwirowe
potencjału skalarnego, którego gradient jest równy
natężeniu pola elektrycznego.
Reinhard Kulessa
38
6. Dywergencję funkcji wektorowej,
7. Prawo Gaussa, również w postaci różniczkowej
8. Twierdzenie Gaussa podające związek pomiędzy całką
powierzchniową a objętościową ,
9. Definicja potencjału skalarnego pola ,
10. Równania Poissona i Laplace’a pozwalające wyliczyć
potencjał pola,
Rozważmy pole elektryczne, dla którego gęstość ładunku
=0. Wtedy dla potencjału spełnione jest równanie
Poissona z =0, czyli równanie Laplace’a, V=0 .
Jednoznaczne znalezienie potencjału wymaga dodatkowo
podania warunków brzegowych, inaczej zawsze można by
podać rozwiązanie V0.
Reinhard Kulessa
39