Wyodrębnienie ośrodków odpowiedzialności w przedsiębiorstwie

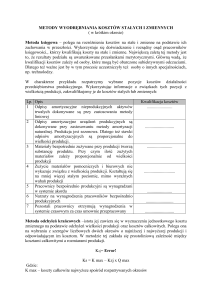
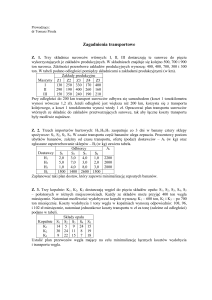
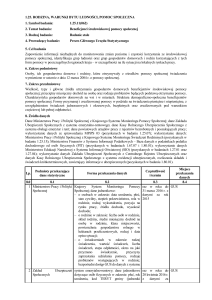
Metody podziału kosztów na zmienne i stałe
KOSZTY STAŁE
 Koszty stałe to koszty, które nie zależą od wielkości produkcji, np. czynsz
dzierżawny, amortyzacja, wynagrodzenia zarządu.
 Koszty stałe jednostkowe maleją wraz ze wzrostem produkcji.
 Gdy firma wykorzystuje w 100% moce produkcyjne koszty jednostkowe stałe są
najniższe - tzw. koszty stałe użyteczne.
 Gdy firma nie wykorzystuje 100% mocy wytwórczych koszty stałe dzielą się na
koszty stałe użyteczne oraz koszty stałe puste (nieużyteczne).
KOSZTY STAŁE CAŁKOWITE I JEDNOSTKOWE
Koszty stałe całkowite
Koszty stałe jednostkowe
Koszty całkowite
Koszty jednostkowe
Wielkość
produkcji
Wielkość
produkcji
WZROST KOSZTÓW STAŁYCH
Koszty stałe całkowite
Wielkość
produkcji
Koszty stałe i zmienne
• Koszty stałe mogą mied charakter kosztów:
- bezwzględnie stałych
- względnie stałych.
• Kosztów bezwzględnie stałych, szczególnie w dłuższych
przedziałach czasu, jest w praktyce stosunkowo niewiele.
• Koszty względnie stałe to koszty stałe w pewnym
przedziale wielkości produkcji, po przekroczeniu którego
następuje ich skok na wyższy poziom.
• Koszty stałe w ujęciu jednostkowym przy wzroście
rozmiarów produkcji zmniejszają się. Zjawisko to nosi
nazwę korzyści skali.
KOSZTY ZMIENNE
 Koszty zmienne to koszty, które zależą od wielkości produkcji.
1) proporcjonalne – wzrastają w tym samym tempie, co produkcja (np.
materiały, płace akordowe)
2) progresywne – wzrastają szybciej niż wzrost produkcji (np. wynagrodzenia w
akordzie progresywnym)
3) degresywne – rosną wolniej niż wzrost produkcji (np. płace w akordzie
degresywnym)
KOSZTY ZMIENNE PROPORCJONALNE
Koszty zmienne całkowite
Koszty zmienne jednostkowe
Koszty całkowite
Koszty jednostkowe
Wielkość
produkcji
Wielkość
produkcji
KOSZTY ZMIENNE PROGRESYWNE
Koszty zmienne całkowite
Koszty zmienne jednostkowe
Koszty całkowite
Koszty jednostkowe
Wielkość
produkcji
Wielkość
produkcji
KOSZTY ZMIENNE DEGRESYWNE
Koszty zmienne całkowite
Koszty zmienne jednostkowe
Koszty całkowite
Koszty jednostkowe
Wielkość
produkcji
Wielkość
produkcji
Zmiennosc kosztów charakteryzuja wskazniki zmiennosci (elastycznosci), które wyrazaja
stosunek wzglednej zmiany danego kosztu do wzglednej zmiany rozmiaru dzialalnosci.
Wzk = K : x
K
x
czyli:
Wzk = % K / % x
gdzie: k-koszt,
x- rozmiary dzialalnosci
Zadanie - przykład
Jeśli
przyrost
kosztów
zmiennych
w
rozpatrywanym okresie wynosi 5%,
natomiast przyrost produkcji – 10% to wskaźnik
zmienności kosztów wynosi:
Wzk = 5/10 = 0,5
oznacza to, że koszty zmienne rosną o połowę
wolniej w stosunku do wzrostu produkcji.
Wskaźniki kosztów wynoszą odpowiednio dla:
a) Kosztów proporcjonalnych 1
b) Kosztów progresywnych powyżej 1
c) Kosztów degresywnych oscylują w przedziale
od 0 do 1.
Metody stosowane w przedsiębiorstwach
Do najczęściej stosowanych metod podziału kosztów na
koszty stałe i koszty zmienne należą:
1. metoda analizy księgowej,
2. metoda pomiaru inżynierskiego,
3. metody statystyczno-matematyczne.
Wyjaśnienie pojęd.
• Metoda analizy księgowej polega na rozróżnieniu kosztów stałych i kosztów
zmiennych na podstawie zachowania się kosztów w przeszłości.
Wykorzystuje się tu doświadczenie i rozsądny osąd pracowników
księgowości, którzy kwalifikują poszczególne rodzaje kosztów na koszty stałe
i koszty zmienne. Największą zaletą metody analizy księgowej jest jej
prostota i stosunkowo mała pracochłonnośd .
• Metoda pomiaru inżynierskiego polega na ustalaniu wielkości zużycia
czynników produkcji na podstawie szczegółowej analizy produktu i procesu
technologicznego. Ustalenia inżynierów są ważne, lecz z reguły
pracochłonne i kosztowne.
• W obrębie metod statystyczno-matematycznych są wykorzystywane różne
metody...
Problem 4.
Określid charakter kosztów (stały- zmienny), jeżeli wielkośd produkcji i koszty jednostkowe
kształtują się następująco:
progukcja
A
B
C
D
E
1
2
1
2
10
10
2
2
1,2
1,8
5
5
3
2
1,3
1,7
3,33
3,33
4
2
1,5
1,6
2,5
5
5
2
1,8
1,5
2
4
Koszty całkowite
Wyodrębnianie kosztów stałych i zmiennych metodą wizualną
KS
Różnica w
kosztach
zmiennych
Różnica w rozmiarach
produkcji
Wielkość produkcji
KS – koszty stałe
Wyodrębnianie kosztów stałych i zmiennych metodą wizualną
• Metoda wizualna polega na narysowaniu linii prostej tak, aby była
najlepiej dopasowana do danych wyjściowych, rozpoczynając jej
kreślenie z punktu charakteryzującego najwyższy poziom kosztów.
• Następnie znajdujemy punkt przecięcia linii z osią pionową –
wysokośd kosztów stałych.
• Wyliczamy koszty całkowite dla produkcji przynoszącej najwyższe
koszty (lub dla produkcji w punkcie, przez który przechodzi nasza
linia). Różnica między kosztami całkowitymi a kosztami stałymi dla
tej wielkości produkcji oznacza wysokośd kosztów zmiennych.
• Koszt zmienny jednostkowy ustalamy dzieląc koszty zmienne przez
rozmiary produkcji odpowiadające przyjętym kosztom całkowitym.
Zadanie
Miesiąc
Wielkość produkcji Koszty całkowite
(X)
(KC)
Lipiec
80
10 200
Sierpień
90
10 900
Wrzesień
100
12 100
Październik
80
10 800
Listopad
120
13 700
Grudzień
110
12 500
Razem
580
70 200
16 000
14 000
12 000
koszt całkowity
10 000
8 000
Serie1
6 000
4 000
2 000
0
0
20
40
60
80
produkcja
100
120
140
16 000
14 000
12 000
koszt całkowity
10 000
8 000
Serie1
6 000
4 000
2 000
0
0
20
40
60
80
produkcja
100
120
140
16 000
14 000
12 000
koszt całkowity
10 000
8 000
Serie1
6 000
4 000
2 000
0
0
20
40
60
80
produkcja
100
120
140
16 000
14 000
12 000
koszt całkowity
10 000
8 000
Serie1
6 000
4 000
Koszty
stałe
2 000
0
0
20
40
60
80
produkcja
100
120
140
16 000
14 000
12 000
koszt całkowity
10 000
Koszty
Serie1
zmienne
8 000
6 000
4 000
Koszty
stałe
2 000
0
0
20
40
60
80
produkcja
100
120
140
METODA WIELKOŚCI KRAOCOWYCH
•
Metoda dwóch punktów krańcowych
(metoda wielkości krańcowych) polega na
wybraniu z szeregów liczbowych dwóch
okresów o najniższej i najwyższej wielkości
produkcji i odpowiadających im kosztów.
METODA WIELKOŚCI KRAOCOWYCH
W metodzie tej koszty zmienne jednostkowe i całkowite koszty stałe
obliczamy następująco:
k zj 
K cmax  K cmin
qmax  qmin
,
Poziom kosztów stałych ustala się, wykorzystując informacje o
krańcowych wielkościach produkcji i odpowiadających im kosztach.
K s  Kcmax  k zj  qmax
gdzie:
Kcmax - koszty całkowite najwyższe spośród rozpatrywanych okresów,
Kcmin - koszty całkowite najniższe spośród rozpatrywanych okresów,
qmax - maksymalna produkcja spośród rozpatrywanych okresów,
qmin - minimalna produkcja spośród rozpatrywanych okresów.
Metoda regresji liniowej – metoda najmniejszych kwadratów(MNK)
Analiza regresji liniowej jest pozbawiona wad prezentowanych poprzednio metod,
• Polega ona na jak najlepszym dopasowaniu linii kosztów do wszystkich obserwacji oraz
określeniu stopnia dopasowania tej linii do tych obserwacji,
• Wykorzystujemy do tego metodę najmniejszych kwadratów (MNK) – poszukujemy naszych
zmiennych obrazujących wysokość kosztów stałych i jednostkowych kosztów zmiennych,
rozwiązując dwa równania z dwiema niewiadomymi:
•
n
n
i 1
n
i 1
 KC  nKS  kz x
n
n
 xKC  KS  x  kz x
i 1
gdzie:
n – liczba obserwacji,
KS – koszty stałe,
x – suma obserwacji wielkości produkcji,
KC – suma obserwacji kosztów całkowitych,
x2 – suma kwadratów obserwacji wielkości produkcji,
kz – jednostkowe koszty zmienne.
i 1
i 1
2
Metoda regresji liniowej – metoda najmniejszych kwadratów(MNK)
kz 
n
n
n
i 1
i 1
i 1
2
n   x  KC   x   KC
n


2
n   x   x 
i 1
 i 1 
n
n
KS 
n
 KC  x
i 1
n

i 1
n
 kz
Metoda regresji liniowej – metoda najmniejszych kwadratów(MNK)
Miesiąc
Wielkość
produkcji
(X)
Lipiec
80
Sierpień
90
Wrzesień
100
Październik
80
Listopad
120
Grudzień
110
Razem
580
Koszty
całkowite
(KC)
10 200
10 900
12 100
10 800
13 700
12 500
70 200
X x KC
X2
816 000
981 000
1 210 000
864 000
1 644 000
1 375 000
6 890 000
6 400
8 100
10 000
6 400
14 400
12 100
57 400
Metody statystyczne:
Jedną z dośd popularnych metod stosowanych przy wydzielaniu kosztów stałych i zmiennych jest
metoda statystyczna. Pozwala ona na podstawie tzw. równania regresji (liniowej lub czasem
nieliniowej) wydzielid częśd stałą kosztów całkowitych oraz częśd zmienną, uzależnioną od skali
produkcji (czy sprzedaży). Warunkiem zastosowania tej metody jest informacja liczbowa z kilku
okresów przeszłych (szereg czasowy), na bazie której budowane jest równanie. W praktyce zazwyczaj
stosuje się równanie regresji liniowej, wychodząc z założenia, że w krótkich odcinkach czasu najlepiej
do przebiegu kosztów całkowitych w zależności od zmian skali produkcji (sprzedaży) jest dopasowana
linia prosta.
Idea metody regresji liniowej jest zawarta w równaniu:
K=v×x+F
gdzie:
K – koszty całkowite,
v – jednostkowe koszty zmienne (przypadające na jednostkę produkcji lub sprzedaży),
x – wielkośd produkcji (lub skala sprzedaży),
F – koszty stałe globalne
V
F
V
F
V
F
V
F
V
F
V
F
V
F