Zgodnie z wcześniejszymi zapowiedziami dyrekcja Oficyny Wydawniczo-Poligraficznej
„Adam” prezentuje nauczycielom uczącym matematyki w gimnazjum rozkłady materiału
dostosowane do nowej podstawy programowej. (Rozporządzenie Ministra Edukacji
Narodowej z dnia 23.08.2007 r. – DzU nr 157, poz. 1100)
KLASA I
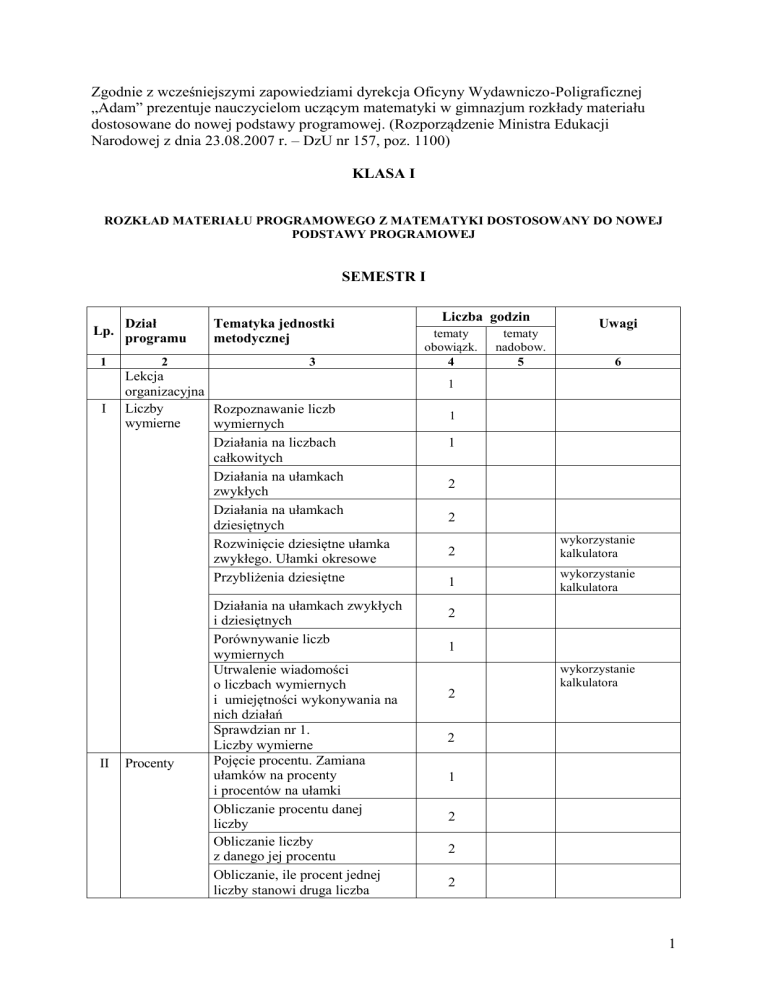
ROZKŁAD MATERIAŁU PROGRAMOWEGO Z MATEMATYKI DOSTOSOWANY DO NOWEJ
PODSTAWY PROGRAMOWEJ
SEMESTR I
Lp.
1
I
II
Dział
programu
2
Tematyka jednostki
metodycznej
3
Lekcja
organizacyjna
Liczby
Rozpoznawanie liczb
wymierne
wymiernych
Działania na liczbach
całkowitych
Działania na ułamkach
zwykłych
Działania na ułamkach
dziesiętnych
Rozwinięcie dziesiętne ułamka
zwykłego. Ułamki okresowe
Przybliżenia dziesiętne
Procenty
Działania na ułamkach zwykłych
i dziesiętnych
Porównywanie liczb
wymiernych
Utrwalenie wiadomości
o liczbach wymiernych
i umiejętności wykonywania na
nich działań
Sprawdzian nr 1.
Liczby wymierne
Pojęcie procentu. Zamiana
ułamków na procenty
i procentów na ułamki
Obliczanie procentu danej
liczby
Obliczanie liczby
z danego jej procentu
Obliczanie, ile procent jednej
liczby stanowi druga liczba
Liczba godzin
tematy
obowiązk.
4
tematy
nadobow.
5
Uwagi
6
1
1
1
2
2
2
wykorzystanie
kalkulatora
1
wykorzystanie
kalkulatora
2
1
wykorzystanie
kalkulatora
2
2
1
2
2
2
1
1
2
3
Oprocentowanie oszczędności
i kredytów
Promile
Próby stopu złota i srebra
Zadania utrwalające wiadomości
o procentach
Sprawdzian nr 2. Procenty
III
Wyrażenia
algebraiczne
Odczytywanie, nazywanie i zapisywanie wyrażeń algebraicznych
Wartość liczbowa wyrażenia
algebraicznego
Jednomiany
Suma algebraiczna. Redukcja
wyrazów podobnych
Dodawanie i odejmowanie
sum algebraicznych
Mnożenie sumy algebraicznej
przez jednomian
Wyłączanie wspólnego
czynnika poza nawias
Działania na wyrażeniach
algebraicznych – powtórzenie
IV Figury
geometryczne.
Podstawowe
konstrukcje
geometryczne.
Sprawdzian nr 4. Wyrażenia
algebraiczne
Twierdzenie – założenie, teza
Konstruowanie prostych prostopadłych i prostych równoległych
Proste równoległe przecięte
trzecia prostą
Dodawanie i odejmowanie
odcinków
Symetralna odcinka i jej własności
Dodawanie i odejmowanie kątów
Dwusieczna kąta i jej własności
Trójkąty i ich własności. Suma
kątów wewnętrznych trójkąta
Okrąg i koło
Wzajemne położenie dwóch
okręgów
Konstruowanie trójkątów z trzech
danych odcinków
Konstruowanie trójkątów z danych dwóch odcinków i kąta zawartego między tymi odcinkami
Konstruowanie trójkątów
z danego odcinka i dwóch
przylegających do niego kątów
4
5
6
3
1
2
3
2
1
2
1
2
2
1
1
1
2
1
1
kąty odpowiadające
i naprzemianległe
2
1
2
2
2
2
1
1
2
I cecha przystawania
trójkątów (b,b,b)
2
II cecha przystawania
trójkątów (b,k,b)
2
III cecha przystawania
trójkątów (k,b,k)
2
1
2
3
4
Zadania konstrukcyjne –
kreślenie wielokątów
Pojęcie kąta wpisanego
i środkowego
Kąt środkowy i kąt wpisany
oparte na tym samym łuku
Kąty wpisane oparte na tym
samym łuku
5
6
2
2
2
1
Kąt wpisany oparty na
półokręgu
Zadania powtórzeniowe –Konstruowanie trójkątów i innych
wielokątów
Sprawdzian nr 3. Figury
geometryczne i podstawowe
konstrukcje geometryczne
1
2
2
SEMESTR II
Lp.
1
V
Dział
programu
2
Równania
i nierówności
Tematyka jednostki
metodycznej
3
Równania. Równania równoważne. Równania tożsamościowe
Rozwiązywanie równań
pierwszego stopnia z jedną
niewiadomą
Nierówności I stopnia z jedną
niewiadomą
Rozwiązywanie nierówności
pierwszego stopnia z jedną
niewiadomą
Zastosowanie równań do
rozwiązywania zadań tekstowych
Zastosowanie nierówności do
rozwiązywania zadań tekstowych
Proporcja i jej własności
Przekształcanie wzorów
VI
Funkcje
Powtórzenie wiadomości o
równaniach i nierównościach
Sprawdzian nr 5. Równania
i nierówności I stopnia z jedną
niewiadomą
Prostokątny układ współrzędnych na płaszczyźnie
Liczba godzin
tematy
obowiązk.
4
tematy
nadobow.
5
Uwagi
6
1
3
1
2
3
1
2
2
Wykorzystywanie
wzorów fizycznych
1
2
1
3
1
VII
2
Symetrie
3
Odczytywanie współrzędnych
punktów i zaznaczanie punktów o danych współrzędnych
Opisywanie zbiorów punktów
w prostokątnym układzie
współrzędnych za pomocą
równań i nierówności
Pojęcie i przykłady funkcji.
Dziedzina i zbiór wartości
funkcji
Sposoby określania funkcji
Funkcja liniowa y = ax, jej
wykres i własności
Przykłady innych funkcji
Wielkości wprost proporcjonalne
Wielkości odwrotnie
proporcjonalne
Powtórzenie wiadomości
o funkcjach
Sprawdzian nr 6. Funkcje
Punkty symetryczne względem
prostej. Oś symetrii
Kreślenie figur symetrycznych
względem prostej
Punkty symetryczne względem
osi układu współrzędnych
Figury osiowosymetryczne. Oś
symetrii figury
Figury symetryczne względem
punktu. Środek symetrii
Kreślenie figur symetrycznych
względem punktu
Punkty symetryczne względem
początku układu współrzędnych
Środek symetrii figury. Figury
środkowosymetryczne
Wielokąty foremne
Zadania powtórzeniowe z symetrii
Sprawdzian nr 7. Symetrie
VIII Graniastosłupy Przypomnienie wiadomości
o graniastosłupach
Obliczanie pól powierzchni
graniastosłupów
Obliczanie objętości
graniastosłupów
Sprawdzian nr 8.
Graniastosłupy
4
5
6
1
2
1
2
3
1
1
1
1
2
2
2
2
2
2
2
2
1
1
2
2
1
3
3
2
4
Uwagi realizacyjne
1. Dotychczasowy plan wynikowy do klasy I nie zmienia się, gdyż zawiera wszystkie
treści i umiejętności, które są podane w nowej podstawie programowej.
2. Podręczniki do nauczania matematyki dla klasy pierwszej „Z Pitagorasem przez
gimnazjum” („Od Pitagorasa do Euklidesa”) wraz z obudową dydaktyczną są
aktualne.
3. W rozdziałach:
Procenty
Promile
Próby złota i srebra
należy potraktować jako tematy nadobowiązkowe:
Figury geometryczne
Proponujemy ten rozdział rozpocząć od dodatkowego tematu
Twierdzenie – założenie, teza
a po temacie
Kreślenie prostych prostopadłych i prostych równoległych
dodatkowo zrealizować temat
Proste równoległe przecięte trzecią prostą
tematy:
Wzajemne położenie dwóch okręgów
Pojęcie kąta środkowego i wpisanego
Kąt środkowy i kąt wpisany i oparte na tym samym łuku
Kąty wpisane oparte na tym samym łuku
Kąt wpisany oparty na półokręgu
należy potraktować jako nadobowiązkowe
Funkcje
Proponujemy ten rozdział rozpocząć od dodatkowych tematów:
Prostokątny układ współrzędnych na płaszczyźnie
Odczytywanie współrzędnych punktów i zaznaczanie punktów o danych
współrzędnych
Opisywanie zbiorów punktów w prostokątnym układzie współrzędnych
za pomocą równań i nierówności
temat
Przykłady innych funkcji
należy potraktować jako temat nadobowiązkowy
4. Należy realizować nowy rozdział:
Graniastosłupy
Przypomnienie wiadomości o graniastosłupach
Obliczanie pól powierzchni graniastosłupów
Obliczanie objętości graniastosłupów
5
Klasa II
ROZKŁAD MATERIAŁU PROGRAMOWEGO Z MATEMATYKI DOSTOSOWANY DO NOWEJ
PODSTAWY PROGRAMOWEJ
SEMESTR I
Dział
Lp.
programu
1
2
Liczba godzin
Tematyka jednostki
metodycznej
3
Lekcja
organizacyjna
I
Potęgi
i pierwiastki
Wyrażenia
algebraiczne
4
tematy
nadobow
.
5
Uwagi
6
1
Potęga o wykładniku naturalnym
Mnożenie i dzielenie potęg
o tych samych podstawach
1
Potęgowanie potęgi
Mnożenie i dzielenie potęg
o tych samych wykładnikach
Określenie pierwiastka kwadratowego z liczby nieujemnej i pierwiastka sześciennego z dowolnej
liczby
Przykłady liczb niewymiernych
1
Pierwiastek z iloczynu i ilorazu.
Iloczyn i iloraz pierwiastków tego
samego stopnia
Wyłączanie czynnika przed znak
pierwiastka i włączanie czynnika
pod znak pierwiastka
Przykłady potęg o wykładniku
całkowitym (ujemnym)
Zapis liczb w postaci
wykładniczej
Przekształcanie wyrażeń zawierających potęgi i pierwiastki
II
tematy
obowiązk.
Sprawdzian nr 1. Potęgi
i pierwiastki
Wyrażenia algebraiczne
i obliczanie ich wartości
liczbowych
Dodawanie i odejmowanie
wyrażeń algebraicznych
Mnożenie sumy algebraicznej
przez jednomian
Mnożenie sum algebraicznych
Wzory skróconego mnożenia
1
1
2
1
2
2
1
1
szacowanie wartości
wyrażeń zawierających pierwiastki
2
2
1
1
1
2
2
6
1
2
3
Przekształcanie wyrażeń
algebraicznych z zastosowaniem
wzorów skróconego mnożenia
Rozkładanie sum algebraicznych
na czynniki
Powtórzenie i utrwalenie
wiadomości o wyrażeniach
algebraicznych
III
Równania
i nierówności
Sprawdzian nr 2. Wyrażenia
algebraiczne
Rozwiązywanie równań
pierwszego stopnia z jedną
niewiadomą
Rozwiązywanie nierówności
pierwszego stopnia z jedną
niewiadomą
Zastosowanie równań i nierówności pierwszego stopnia z jedną
niewiadomą do rozwiązywania
zadań tekstowych
Powtórzenie i utrwalenie
wiadomości o równaniach
i nierównościach
IV
V
Proste i trójkąty w relacji
z okręgiem
Odcinki proporcjonalne.
Twierdzenie
Talesa
Sprawdzian nr 3. Równania
i nierówności pierwszego
stopnia z jedną niewiadomą
Okrąg i prosta. Styczna do okręgu
Konstrukcja okręgu opisanego na
trójkącie
Konstrukcja okręgu wpisanego
w trójkąt
Powtórzenie wiadomości o okręgu
opisanym na trójkącie i okręgu
wpisanym w trójkąt
Sprawdzian nr 4. Proste i trójkąty
w relacji z okręgiem
Stosunek dwóch wielkości tego
samego rodzaju
Podział odcinka na równe części
Proporcjonalność odcinków utwozonych na ramionach kątów
przeciętych prostymi równoległymi. Twierdzenie Talesa
Zastosowanie twierdzenia
Talesa do rozwiązywania zadań
Zadania powtórzeniowe
Sprawdzian nr 5. Odcinki
proporcjonalne. Twierdzenie
Talesa
4
5
6
2
1
bez wzorów skróconego mnożenia
1
2
3
3
5
1
2
2
2
2
2
2
1
2
3
5
1
2
7
SEMESTR II
Dział
Lp. programu
1
VI
2
Tematyka jednostki
metodycznej
3
Jednokładność Punkty i figury jednokładne
i podobieńKreślenie figur jednokładnych
stwo
Punkty jednokładne względem
początku układu współrzędnych
Twierdzenie
Pitagorasa
VIII Pola figur
płaskich
Trójkąty prostokątne podobne
Cechy podobieństwa trójkątów
1
2
1
IX
Ostrosłupy
1
2
Konstrukcja kwadratów na
bokach trójkąta prostokątnego.
Twierdzenie Pitagorasa
2
Twierdzenie odwrotne do
twierdzenia Pitagorasa
1
Zastosowanie twierdzenia Pitagorasa do rozwiązywania zadań
3
Powtórzenie twierdzenia
Pitagorasa
1
2
7
Pola wielokątów foremnych
2
Długość okręgu i pole koła
3
Kreślenie siatek i sporządzanie
modeli ostrosłupów
Obliczanie pól powierzchni
ostrosłupów
6
1
Sprawdzian nr 6. Jednokładność
i podobieństwo
Powtórzenie wiadomości o
polach wielokątów, długości
okręgu, polu koła
Sprawdzian nr 8. Pola wielokątów, długość okręgu i pole koła
Pojęcie ostrosłupa. Wierzchołki,
krawędzie, podstawa, ściany
boczne
Kreślenie ostrosłupów
Uwagi
1
1
Sprawdzian nr 7. Twierdzenie
Pitagorasa
Obliczanie pól wielokątów
tematy
nadobow.
5
1
1
Figury podobne i ich własności
Podobieństwo prostokątów
Stosunek pól figur podobnych
Powtórzenie jednokładności
i podobieństwa figur
VII
Liczba godzin
tematy
obowiązk.
4
2
2
2
1
1
3
8
1
2
3
4
Obliczanie objętości
ostrosłupów
5
6
3
Powtórzenie wiadomości
o ostrosłupach
Sprawdzian nr 9. Ostrosłupy
2
2
Uwagi realizacyjne
1. Dotychczasowy plan wynikowy do klasy II nie zmienia się, gdyż zawiera wszystkie
treści i umiejętności, które są podane w nowej podstawie programowej.
2. Podręczniki do nauczania matematyki dla klasy drugiej „Z Pitagorasem przez
gimnazjum” ( „Od Pitagorasa do Euklidesa”) wraz z obudową dydaktyczną są
aktualne.
3. W rozdziale
Potęgi i pierwiastki
Przykłady liczb niewymiernych
należy potraktować jako temat nadobowiązkowy, a po temacie
Przykłady potęg o wykładniku całkowitym
dodatkowo zrealizować temat
Zapis liczb w postaci wykładniczej
Wyrażenia algebraiczne
Wzory skróconego mnożenia
Przekształcanie wyrażeń algebraicznych z zastosowaniem wzorów skróconego
mnożenia
należy potraktować jako tematy nadobowiązkowe.
Jednokładność i podobieństwo
po temacie
Trójkąty prostokątne podobne
należy dodatkowo zrealizować temat
Cechy podobieństwa trójkątów
KLASA III
ROZKŁAD MATERIAŁU PROGRAMOWEGO Z MATEMATYKI DOSTOSOWANY DO NOWEJ
PODSTAWY PROGRAMOWEJ
SEMESTR I
Lp.
1
Dział
programu
2
Tematyka jednostki
metodycznej
3
Lekcja
organizacyjna
I
Funkcje
Liczba godzin
tematy
obowiązk.
4
tematy
nadobow.
5
Uwagi
6
1
Przypomnienie wiadomości
o funkcji
2
9
1
2
3
Funkcja liniowa i y = ax + b
i jej wykres
Własności funkcji liniowej
Powtórzenie wiadomości
o funkcji liniowej
Sprawdzian nr 1. Funkcje
II Układy równań Równania pierwszego stopnia
liniowych
z dwiema niewiadomymi
Układy dwóch równań pierwszego stopnia z dwiema niewiadomymi. Równoważność
układów równań
Rozwiązywanie układu dwóch
równań pierwszego stopnia
z dwiema niewiadomymi
Układ równań oznaczony,
nieoznaczony i sprzeczny
Zastosowanie układów równań
liniowych do rozwiązywania
zadań tekstowych
Powtórzenie wiadomości
o równaniach I stopnia z dwiema
niewiadomymi i układach
równań liniowych
Sprawdzian nr 2. Równania
I stopnia z dwiema niewiadomymi i układy równań liniowych
III Proste
Wzajemne położenie dwóch
i płaszczyzny prostych w przestrzeni
w przestrzeni Wzajemne położenie prostej
i płaszczyzny oraz dwóch
płaszczyzn w przestrzeni
Kąt między prostą i płaszczyzną
Kąt dwuścienny i jego miara
IV Pola powierzPrzypomnienie wiadomości
chni i objętości o graniastosłupach
graniastosłupów Przypomnienie wiadomości
o ostrosłupach
i ostrosłupów
Zadania na obliczanie pól
powierzchni objętości graniastosłupów i ostrosłupów
Sprawdzian nr 3. Graniastosłupy
i ostrosłupy
4
5
6
3
3
2
2
2
1
4
3
5
2
2
1
1
2
2
3
3
4
2
10
SEMESTR II
Lp.
1
V
VI
Dział
programu
Tematyka jednostki
metodycznej
2
Bryły
obrotowe
Elementy
statystyki
3
Walec – jego pole powierzchni
i objętość
Stożek – jego pole powierzchni
i objętość
Kula – jej pole powierzchni
i objętość
Powtórzenie wiadomości
o bryłach obrotowych
Sprawdzian nr 4. Bryły
obrotowe
Zbieranie i porządkowanie
danych
Graficzne przedstawianie
danych
Odczytywanie i analizowanie
danych
Obliczanie średniej arytmetycznej, rozstępu, dominanty
i mediany
Przykłady doświadczeń
losowych
Sprawdzian nr 5. Elementy
statystyki
Liczba godzin
tematy
obowiązk.
4
tematy
nadobow.
5
Uwagi
6
4
4
3
3
2
3
4
3
4
4
2
Uwagi realizacyjne
1. Dotychczasowy plan wynikowy do klasy III nie zmienia się, gdyż zawiera wszystkie
treści i umiejętności, które są podane w nowej podstawie programowej.
2. Podręczniki do nauczania matematyki dla klasy trzeciej „Z Pitagorasem przez
gimnazjum” („Od Pitagorasa do Euklidesa”) wraz z obudową dydaktyczną są
aktualne.
3. Pozostałe godziny w klasie III należy przeznaczyć na powtórzenie całego materiału
z matematyki realizowanego w gimnazjum i jak najlepiej przygotować ucznia
do egzaminu zewnętrznego.
11