wydzia* zarz*dzania i informatyka

Druk DNiSS nr PK_10
OPIS MODUŁU KSZTAŁCENIA (SYLABUS)
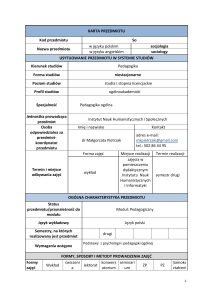
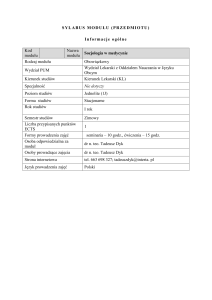
NAZWA MODUŁU KSZTAŁCENIA/PRZEDMIOTU: MATEMATYKA I
Kod przedmiotu: ISP2
Rodzaj przedmiotu: podstawowy; obowiązkowy
Wydział: Inżynierii Materiałów, Budownictwa i Środowiska
Kierunek: Inżynieria Środowiska
Specjalność (specjalizacja): wszystkie
Poziom studiów: pierwszego stopnia
Profil studiów: ogólnoakademicki
Forma studiów: niestacjonarne
Rok: I Semestr: II
Formy zajęć i liczba godzin: wykłady – 18; ćwiczenia audytoryjne - 18;
Język/i, w którym/ch realizowane są zajęcia: polski
Liczba punktów ECTS: 6
Osoby prowadzące:
wykład: dr Celina Rom ([email protected])
inne formy zajęć: dr Celina Rom ([email protected])
1. Założenia i cele przedmiotu
Zapoznanie się z podstawowymi pojęciami z zakresu analizy matematycznej i algebry wraz z
ich zastosowaniami w naukach przyrodniczych i technicznych, podniesienie poziomu
sprawności rachunkowej, umiejętność interpretacji otrzymanych wyników.
2. Określenie przedmiotów wprowadzających wraz z wymaganiami wstępnymi
Matematyka w zakresie szkoły średniej i semestru pierwszego.
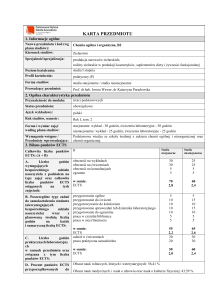
3. Opis sposobu wyznaczania punktów ECTS
Forma aktywności
Godziny kontaktowe: uczestnictwo w zajęciach (wykłady + ćwiczenia)
Przygotowanie bieżące do ćwiczeń
Przygotowanie do kolokwiów
Przygotowanie do egzaminu
Suma godzin
Liczba punktów ECTS dla modułu (przedmiotu)
Liczba godzin
36 (18+18)
48
48
48
180
6
4. Wskaźniki sumaryczne
a) liczba godzin dydaktycznych (tzw. kontaktowych) i liczba punktów ECTS na zajęciach
wymagających bezpośredniego udziału nauczycieli akademickich, realizowanych w formie
studiów stacjonarnych i niestacjonarnych.
Uczestniczenie w wykładach - 18 godzin.
Uczestniczenie w ćwiczeniach audytoryjnych – 18 godzin.
Razem 36 godzin. Odpowiada to 1 punktom ECTS.
b) liczba godzin dydaktycznych (tzw. kontaktowych) i liczba punktów ECTS na zajęciach o
charakterze praktycznym (ćwiczeniach audytoryjnych, laboratoryjnych, projektowych itp.).
Uczestniczenie w ćwiczeniach audytoryjnych – 18 godzin.
Przygotowanie bieżące do ćwiczeń – 48 godzin.
Przygotowanie do kolokwiów – 48 godzin.
1
Przygotowanie do egzaminu – 48 godzin.
Razem 162 godziny. Odpowiada to 5 punktom ECTS.
5. Zakładane efekty kształcenia
Numer
(Symbol)
P_W01
P_W02
Odniesienie
do efektów
kształcenia
dla kierunku
Efekty kształcenia dla przedmiotu
WIEDZA
Ma uporządkowaną wiedzę w zakresie algebry, w
szczególności:
- liczb zespolonych,
- algebry liniowej,
Ma uporządkowaną wiedzę w zakresie analizy
matematycznej, w szczególności:
- rachunku różniczkowego funkcji dwóch i trzech
zmiennych oraz jego zastosowań,
IS1A_W01
IS1A_W01
.
P_U01
UMIEJĘTNOŚCI
Potrafi wykorzystać poznane metody i modele
matematyczne do analizy podstawowych zagadnień
fizycznych i technicznych, w szczególności:
- umie korzystać z rachunku macierzowego,
rozwiązywać układy równań liniowych,
- umie korzystać z rachunku różniczkowego funkcji
dwóch i trzech zmiennych w celu rozwiązywania
zadań optymalizacyjnych,
IS1A_U01,
IS1A_U05,
IS1A_U11
6. Odniesienie efektów kształcenia do form zajęć i sposób oceny osiągnięcia przez
studenta efektów kształcenia
Numer
(Symbol)
P_W01
P_W02
P_U01
Efekty kształcenia dla przedmiotu
WIEDZA
. Ma uporządkowaną wiedzę w zakresie algebry, w
szczególności:
- liczb zespolonych,
- algebry liniowej
Ma uporządkowaną wiedzę w zakresie analizy
matematycznej, w szczególności:
- rachunku różniczkowego funkcji dwóch i trzech
zmiennych oraz jego zastosowań,
UMIEJĘTNOŚCI
Potrafi wykorzystać poznane metody i modele
2
Odniesienie
do form zajęć
Wykłady,
ćwiczenia
Wykłady,
ćwiczenia
Wykłady,
Sposób oceny
Egzaminy,
kolokwia,
odpowiedzi
ustne, prace
domowe
Egzaminy,
kolokwia,
odpowiedzi
ustne, prace
domowe
Egzaminy,
matematyczne do analizy podstawowych zagadnień
fizycznych i technicznych, w szczególności:
- umie korzystać z rachunku macierzowego,
rozwiązywać układy równań liniowych,
- umie korzystać z rachunku różniczkowego funkcji
dwóch i trzech zmiennych w celu rozwiązywania
zadań optymalizacyjnych,
ćwiczenia
kolokwia,
odpowiedzi
ustne, prace
domowe
7. Opis sposobu weryfikacji osiągniętych przez studenta założonych dla przedmiotu
efektów kształcenia (należy opisać sposób weryfikacji każdego efektu kształcenia oddzielnie)
Nazwa
Sposobu
Odpowiedź ustna
Praca domowa
Kolokwium
Egzamin (ustny lub
pisemny)
Opis
Efekty kształcenia
Sprawdzanie znajomości treści wykładów
i umiejętności ich zastosowania w praktyce
poprzez zadawanie pytań przez prowadzącego
Sprawdzanie znajomości rozwiązywania zadań
domowych
Sprawdzanie umiejętności na podstawie
analizy rozwiązywanych zadań w trakcie
kolokwiów
Sprawdzanie znajomości pojęć i twierdzeń
i umiejętności rozwiązywania zadań w oparciu
o analizę odpowiedzi na pytania egzaminacyjne
o charakterze teoretycznym i praktycznym
P_W01, P_W02, P_U01
P_W01, P_W02, P_U01
P_W01, P_W02, P_U01
P_W01, P_W02, P_U01
8. Opis zasad zaliczania przedmiotu i sposobu ustalania oceny końcowej z przedmiotu
Do pierwszego i drugiego terminu egzaminu dopuszczone są osoby mające zaliczenie.
Egzamin w trzecim terminie zdają także osoby nie mające zaliczenia, które uzyskują na
podstawie zdanej części praktycznej egzaminu.
Ocena końcowa jest zaokrągloną w górę średnią arytmetyczną ocen uzyskanych z zaliczenia
i wszystkich terminów egzaminu.
9. Opis form zajęć
a) Wykłady
 Treści programowe:
1. Rachunek całkowy funkcji jednej zmiennej: definicja, własności oraz interpretacja
geometryczna całki oznaczonej, związek między całką oznaczoną a nieoznaczoną,
twierdzenia o wartości średniej, całki niewłaściwe, zastosowanie geometryczne całki
oznaczonej. ( 4 godziny)
2. Liczby zespolone: określenie zbioru liczb zespolonych, działania w zbiorze liczb
zespolonych, interpretacja geometryczna liczby zespolonej, postać kartezjańska i
geometryczna liczby zespolonej, potęgowanie i pierwiastkowanie liczby zespolonej, postać
wykładnicza liczby zespolonej. ( 3 godziny)
3. Elementy algebry liniowej: macierze, wyznaczniki, układy równań linowych. ( 4 godziny)
4. Przekształcenia liniowe, wartości i wektory własne, diagonalizacja macierzy. ( 3 godziny)
3
5. Rachunek różniczkowy funkcji wielu zmiennych: granica, ciągłość, pochodne cząstkowe
i ekstrema funkcji wielu zmiennych. Funkcje uwikłane. Zastosowania rachunku
różniczkowego do rozwiązywania problemów ekstremalnych w technice. ( 4 godziny)
 Metody dydaktyczne i sposób organizacji zajęć:
Wykład klasyczny uzupełniony prezentacją i materiałami pomocniczymi.
 Wymagania egzaminacyjne:
Uzyskanie 50% punktów z egzaminu.
 Wykaz literatury podstawowej i uzupełniającej:
LITERATURA PODSTAWOWA
1. T. Zgraja, Matematyka dla studentów Wydziału Nauk o Materiałach i Środowisku. Część II,
(w przygotowaniu).
LITERATURA UZUPEŁNIAJĄCA
1. K. Dobrowolska, W. Dyczka, H. Jakuszenkow, Matematyka dla studentów studiów
technicznych. 2, HELPMATH, Łódź 1995.
2. J. Ger, Kurs matematyki dla chemików, Skrypty Uniwersytetu Śląskiego nr 516,
Wydawnictwo Uniwersytetu Śląskiego, Katowice 1996.
3. R. Leitner, Zarys matematyki wyższej dla studentów. Część I, II, WNT, Warszawa 1994.
4. Matematyka dla studentów politechnik: M. Gewert, Z. Skoczylas, Analiza matematyczna 2,
T. Jurlewicz, Z. Skoczylas, Algebra liniowa 1,2, Oficyna Wydawnicza GiS, Wrocław 2002.
5. D. McQuarrie, Matematyka dla przyrodników i inżynierów. 1, 2, PWN, Warszawa 2005.
b) Ćwiczenia audytoryjne
 Treści programowe:
1. Rachunek całkowy funkcji jednej zmiennej. ( 2 godziny)
2. Liczby zespolone. ( 2 godziny)
3. Elementy algebry liniowej. ( 3 godziny)
4. Kolokwium. (2 godziny)
5. Przekształcenia liniowe, wektory i wartości własne, diagonalizacja macierzy. ( 3 godziny)
6. Elementy rachunku różniczkowego funkcji wielu zmiennych. ( 4 godziny)
7. Kolokwium. (2 godziny)
 Metody dydaktyczne:
Rozwiązywanie zadań zarówno przez prowadzącego, jak i uczestników.
 Forma i warunki zaliczenia:
Uzyskanie 50% punktów z kolokwiów i 80% obecności na ćwiczeniach.
 Wykaz literatury podstawowej i uzupełniającej:
LITERATURA PODSTAWOWA
1. Ćwiczenia z analizy matematycznej z zastosowaniami. I, II, Praca zbiorowa pod redakcją
L. Siewierskiego, Warszawa 1979.
2. W. Krysicki, L. Włodarski, Analiza matematyczna w zadaniach. I, II, PWN, Warszawa
1994.
3. R. Leitner, W. Matuszewski, Z. Rojek, Zadania z matematyki wyższej. I, II, WNT,
Warszawa 1994 (I), 1999 (II).
LITERATURA UZUPEŁNIAJĄCA
1. Matematyka dla studentów politechnik: M. Gewert, Z. Skoczylas, Analiza matematyczna 2,
T. Jurlewicz, Z. Skoczylas, Algebra liniowa 1,2, Oficyna Wydawnicza GiS, Wrocław 2002.
4