Równowaga rynkowa w krótkim okresie czasu
1. Funkcja podaży
W poprzednim wykładzie zostało pokazane jak będzie się zmieniać optymalna wielkość
produkcji pojedynczego przedsiębiorstwa działającego na rynku o doskonałej konkurencji, gdy cena
rynkowa będzie ulegała zamianie. Na podstawie przeprowadzonej tam analizy możemy określić, jak
wyglądałaby funkcja określająca zależność między ceną rynkową a wielkością produkcji konkretnej
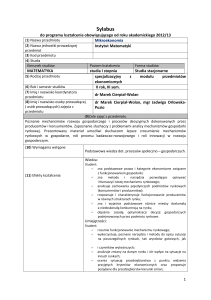
firmy. Zależność między ceną danego produktu a wielkością dostaw na rynek, czyli podażą,
będziemy nazywali funkcją podaży.
Skoro dla ceny p1 optymalna była wielkość produkcji y1* a dla p2 - y2*, podobnie dla p3 - y3*, to
łatwo jest stwierdzić, że rozpatrując nie trzy poziomy ceny ale nieskończenie wiele, otrzymamy
odpowiedni fragment funkcji kosztów krańcowych jako obraz funkcji podaży. Prezentuje to rys. 1.
Dokładniej trzeba wyjaśnić, dlaczego cała funkcja kosztów
p
krańcowych nie stała się funkcją podaży? Należy sobie
Kc’
przypomnieć, co stwierdziliśmy o cenie progu zamknięcia,
oznaczonej symbolem p3. Powiedzieliśmy, że jeżeli cena
rynkowa spadnie poniżej tego poziomu, to producentowi
opłaca się jak najszybciej zlikwidować produkcję tego
wyrobu. Jest to jednoznaczne z tym, że dla cen niższych niż
p1
p3 dany producent nie będzie dostarczał swoich wyrobów na
P2
rynek, czyli podaż będzie równa 0. Dlatego funkcja podaży
P3
jest tylko tym fragmentem krzywej kosztów
krańcowych,
który
leży
powyżej
ceny
progu
zamknięcia, czyli powyżej punktu przecięcia się Kc’ z
Kzp.
y3* y2* y1*
y
Możemy więc stwierdzić bardziej ogólnie, że przebieg
funkcji
podaży pojedynczego producenta zależy od przebiegu
Rys. 1.
jego funkcji kosztów całkowitych, gdyż to one wyznaczają
przebieg kosztów krańcowych.
2. Agregacja funkcji podaży
W dalszej części analizy będziemy prezentować zagadnienie równowagi na rynku danego dobra.
Aby tego dokonać musimy wiedzieć jak będzie wyglądała funkcja podaży wszystkich producentów
danego dobra, czyli musimy dokonać agregacji (zsumować) pojedyncze funkcje podaży. Celem tych
rozważań jest przypomnienie procedury tworzenia zagregowanych funkcji, w tym wypadku podaży 1,
jak również sformułowanie wniosku, określającego, czym mogą się różnić zagregowane funkcje podaży
od indywidualnych.
p4
p
p3
p2
p1
yA1 yA2
yB1
yB2
yA3 yA4 yA,yB
yA1 yA2
yA2+yB1
Rys. 2.
1
Wcześniej mówiliśmy o agregacji indywidualnych funkcji popytu.
yA3+yB2 yA4+yB2 yA+yB
2
Rozpatrzmy najprostszy przypadek, tzn., gdy sumujemy tylko dwie funkcje podaży i gdy są one
Kc2 2. Jeżeli na rynku obowiązywałaby cena niższa niż p , to wtedy dostaw na
prostymi. Prezentuje to rys.
1
rynek nie byłoby, czyli podaż równałaby się zero. Gdyby cena wzrosła do poziomu p1, to wtedy na rynku
Kc1
pojawiłaby się tylko podaż producenta
A w ilości yA1. Dopóki cena jest niższa niż p2 ale na rynku
sprzedaje tylko producent A. Dlatego dla cen od p1 do p2 zagregowana funkcja podaży jest
odpowiednim fragmentem indywidualnej funkcji podaży producenta A. W przedziale cen od p2 do p3
obaj dostawcy oferują swoje produkty i tym samym zagregowana podaż jest sumą ich indywidualnych
podaży. Jak łatwo dostrzec ten fragment zagregowanej funkcji podaży musi być bardziej płaski niż
każdy z odpowiadających mu fragmentów prostej yA i yB. Producent B może maksymalnie
wyprodukować yB2 i dlatego wzrost ceny ponad p3 nie będzie powodował przyrostu jego podaży. Znowu
więc zagregowana podaż z odcinka między cenami p3 i p4 będzie powieleniem odpowiedniego
y
fragmentu indywidualnej funkcji podaży
producenta A. Gdy cena rynkowa przekroczy wysokość p4, to
obie firmy nie będą w stanie zwiększyć dostaw, dlatego podaż utrzyma się na stałym poziomie yA4+yB2.
Im więcej rozpatrywalibyśmy funkcji podaży, to zagregowana podaż tym bardziej
przypominałaby krzywą o rosnącym nachyleniu, czyli taką jak na rys. (odwołanie do indywidualnej
Kc2’
funkcji podaży). Taka tendencja
wystąpiłaby również wtedy, gdyby indywidualne funkcje podaży
byłyby prostymi. Im większą ilość prostych sumujemy, tym częściej (gęściej) wypadają punkty łączące
poszczególne fragmenty prostych i tym samym taka linia łamana coraz bardziej przypomina krzywą z
rys. 1.
Kc1’
Podsumowując: Sumaryczna funkcja podaży przebiega bardziej płasko niż każda z wyjściowych.
3. Wpływ zmian kosztów produkcji na przebieg zagregowanej funkcji podaży
Wykorzystując wcześniej sformułowane wnioski ustalimy teraz, jak na przebieg
zagregowanej funkcji podaży wpływa zmiana kosztów produkcji. Stwierdziliśmy, że wzrost
y warunkach przesuwa funkcję kosztów krańcowych w prawo
kosztów produkcji w typowych
do góry, co przypomina
Rys. 3. jeszcze raz rys. 3.
Wiemy również, że indywidualna funkcja podaży to
jest ten fragment funkcji kosztów krańcowych
producenta, która leży powyżej progu zamknięcia,
czyli powyżej punktu przecięcia się Kc’ i Kzp. Na rys. 3
funkcje podaży zostały przedstawione w postaci
pogrubionych fragmentów kosztów krańcowych.
Jeżeli takie zmiany wystąpią u wszystkich
producentów albo przynajmniej u większości, to
zmieni się przebieg zagregowanej funkcji podaży. W
stosunku do poprzedniej przesunie się ona w lewo do
góry, co oznacza, że podaż pojawi się na rynku dla
wyższej niż poprzednio ceny i będzie jej mniej
(oczywiście, gdy porównujemy wielkości dostaw przy
danej cenie). Jest to stwierdzenie, na które będziemy
się powoływali w dalszej części skryptu.
4. Wyznaczenie punktu równowagi rynkowej
Typowa funkcja podaży jest rosnąca, czyli wzrost ceny wywołuje wzrost podaży. Natomiast
typowa funkcja popytu jest malejąca, tzn. im cena jest wyższa tym mniej danego towaru chcą kupić
nabywcy. Aby się przekonać, gdzie jest punkt równowagi rynkowej najlepiej jest narysować w jednym
3
układzie współrzędnych funkcję popytu na dany produkt i funkcję jego podaży. Taki przykład
prezentuje rys. 4.
W przedstawionym przypadku obie funkcje przecinają się.
p
Zastanówmy się, czym się ten punkt wyróżnia spośród innych.
Y>X Y
X
Zacznijmy rozważania od ceny wyższej niż p*, czyli od ceny p1. Z
analizy rysunku wynika, że dla każdej ceny wyższej niż p* podaż
byłaby większa niż popyt. Co to oznacza dla producentów? Jest to
p1
równoznaczne z tym, że nie wszystkie wyprodukowane przez nich
towary znajdą swoich nabywców. Takiej ilości danego wyrobu Y1
nabywcy po cenie p1 nie kupią. Są skłonni nabyć tylko X1 tego
Y<X
p*
produktu. Różnica między Y1 a X1 będzie zalegała w magazynach.
Producenci ponoszą z tego tytułu straty. Aby je zmniejszyć będą
p2
skłoni obniżać stopniowo cenę na swoje wyroby. Przedsiębiorca,
który to pierwszy uczyni sprzeda całą swoją produkcję, gdyż
nabywcy na homogenicznym rynku mając do wyboru wyroby od
X,
Y
X1
X* = Y* Y1
różnych dostawców wybiorą zawsze produkt, tego który sprzedaje
Rys. 4.
swój towar po niższej cenie. To pogłębi trudności ze zbytem
wszystkich tych przedsiębiorstw, które nie obniżyły ceny. Ten fakt
w typowych warunkach wymusi obniżkę cen wyrobów wszystkich producentów. Jeżeli cenę swojego
wyrobu obniży tylko jeden producent, to sprzeda on całą swoją produkcję. Gdy wszyscy pozostali
wytwórcy obniżą cenę do tego poziomu to nie jest pewne, czy sprzedadzą całą swoją produkcję.
Obniżenie ceny na pewno zwiększy popyt i jednocześnie zmniejszy podaż, gdyż przy niższej cenie
producentom najbardziej opłaca się produkować mniejsze ilości danego wyrobu. Ustanowienie nowej
niższej ceny ale nadal wyższej niż p* zmniejszy wprawdzie nadwyżkę podaży nad popytem ale jej nie
zlikwiduje. Dopiero wtedy wszystkie produkty znajdą nabywców.
Gdyby z kolei cena wyjściowa była niższa niż p*, czyli wynosiła np p2, to wtedy mielibyśmy
odwrotną do poprzedniej sytuację. Teraz występowałaby nadwyżka popytu nad podażą. Co to oznacza
dla nabywców? Najkrócej mówiąc braki towaru w sklepie. Tylko pierwsi klienci dokonaliby zakupu. Dla
przychodzących później towaru zabrakłoby. Efektem tego byłyby kolejki osób oczekujących na dostawę
towaru. Tego typu sytuacje w gospodarce rynkowej występują niezwykle rzadko2, gdyż wtedy można
oczekiwać, że któryś z nabywców, dla którego zabrakło towaru zaproponuję producentom cenę wyższą
od p2. Wtedy oczywiście w pierwszej kolejności zostanie zaspokojony jego popyt. Tym samym pogłębią
się trudności z kupnem danego wyrobu przez tych nabywców, którzy chcą kupować po niższej cenie p2.
Efektem tego będzie zgoda nabywców na podwyżkę ceny. Jeżeli cena wzrośnie do poziomu niższego niż
p*, to wprawdzie popyt zmaleje a podaż wrośnie (czyli nadmiar popytu nad podażą zmniejszy się) ale
nadal popyt będzie większy niż podaż, co będzie wywoływało tendencje do wzrostu ceny.
O punkcie przecięcia się funkcji popytu i podaży możemy więc powiedzieć, że wyznacza on taki
poziom ceny, przy którym podaż jest równa popytowi, co oznacza, że przy cenie równowagi
producenci dążący do maksymalizacji zysku są skłonni produkować dokładnie tyle ile
nabywcy chcą kupić. Oznacza to jednocześnie, że na rynku został osiągnięty maksymalny
poziom ilości sprzedanych produktów, przy ustalonych funkcjach podaży i popytu.
Aby to pokazać wróćmy jeszcze raz do rys. 4. Jeżeli cena na rynku byłaby wyższa niż p*, to
wtedy obroty na rynku (w ujęciu ilościowym a nie wartościowym) będą się równały nie wielkości podaży
ale wielkości popytu, gdyż tylko tyle produktów zostanie sprzedanych. Z kolei jeżeli cena byłaby niższa
niż p* to wtedy wielkość obrotów na rynku będzie pokazywała funkcja podaży, gdyż zostanie
sprzedanych tylko tyle produktów ile wyprodukują dostawcy a nie tyle ile byliby skłonni nabyć klienci.
Tak patrząc na funkcje podaży i popytu dostrzegamy, że największe obroty zostaną osiągnięte na
rynku, gdy cena będzie wynosiła p*, czyli maksymalny obrót wyznacza wielkość X* albo Y* (obie są
sobie równe).
Punkt równowagi można więc scharakteryzować również następująco. Jest to taki punkt w
którym jednocześnie nabywcy kupią najwięcej danego wyrobu a oferenci sprzedadzą
największą ilość swoich wyrobów.
Myląca może się okazać krótsza definicja: równowaga rynkowa występuje wtedy, gdy podaż jest
równa popytowi. Na czym polega możliwość błędnej interpretacji takiego wyrażenia zostanie pokazane
w następnym punkcie.
5. Stabilność równowagi rynkowej
Dotąd formułowaliśmy wnioski w oparciu o analizę typowego przebiegu funkcji podaży i popytu.
W tym punkcie rozpatrzmy również mniej typowe sytuacje i na ich bazie wyjaśnimy zjawisko stabilności
2
Były natomiast typowe dla gospodarki socjalistycznej.
4
i niestabilności równowagi rynkowej. Równowaga rynkowa jest stabilna wtedy, gdy układ
wytrącony z punktu równowagi samoczynnie do niego powraca w wyniku działania
mechanizmu rynkowego.
Najpierw zacznijmy od przypomnienia poprzednio rozważanej sytuacji, czyli gdy obie funkcje
podaży i popytu są typowe. Prezentuje to rys. 5.
Jeżeli w wyniku działania czynników zewnętrznych cena
p
wzrosłaby do poziomu wyższego niż p*, to wtedy wystąpi
Y
X
nadwyżka podaży nad popytem. Ta nadprodukcja będzie tym
większa im cena rynkowa bardziej oddali się od p* (cena
równowagi rynkowej). Jeżeli część oferentów obniży cenę na
swoje wyroby, to tym samym zapewni sobie wzrost
sprzedaży i jednocześnie powiększy problemy ze sprzedażą
tych przedsiębiorstw, które nie obniżyły ceny. To
najprawdopodobniej wymusi na pozostałych oferentach
p*
obniżkę cen. Im większa jest nadprodukcja tym oferenci są
skłonni szybciej i mocniej obniżyć cenę, gdyż utrzymanie
obecnego stanu grozi im dużymi stratami. Tym samym
możemy stwierdzić, że im mocniej cena rynkowa oddali się w
X, Y
X* = Y*
górę od ceny równowagi, tym większe siły rynkowe będą
działały w kierunku jej (ceny rynkowej) obniżenia.
Rys. 5.
Z drugiej strony, gdyby w wyniku tych działań cena
rynkowa spadła poniższej p*, to wystąpi odwrotna sytuacja,
czyli będzie nadwyżka popytu nad podażą. Z punktu widzenia producentów jest to wygodna dla nich
sytuacja, gdyż teraz nie mają żadnych problemów ze zbytem, wręcz odwrotnie nie mogą zaspokoić
wszystkich zamówień. Zwiększenie produkcji przy tej cenie nie opłaca się im, gdyż prowadziłoby do
zmniejszenia ich zysku. Jeżeli na rynku jest nadmiar popytu nad podażą, to część nabywców
zaproponuje wyższe ceny na dany produkt, co pozwoli im zaspokoić ich popyt ale zwiększy trudności z
zakupem tego towaru przez innych nabywców. To wywoła wzrost ceny. Sprzedając po wyższej cenie
będą produkowali więcej, gdyż jak to wcześniej stwierdziliśmy, im wyższa jest cena, tym większa jest
wielkość produkcji, która maksymalizuje zysk. Tendencja do wzrostu ceny będzie on tym większa im
większa była nadwyżka popytu nad podażą. Możemy więc stwierdzić, że na wychylenie się ceny poniżej
ceny równowagi rynek odpowie wystąpieniem sił działających w kierunku wzrostu ceny.
Rynek o doskonałej konkurencji znajduje punkt równowagi metodą prób i błędów. W
przypadku typowego przebiegu funkcji podaży i popytu wystąpią siły samoczynnie przywracające stan
równowagi. Poprzez analogie ten mechanizm można porównać do sprężyny, która ściśnięta
samoczynnie powróci po pewnym czasie do punktu wyjścia. Wtedy też obowiązuje zasada, że im
bardziej jest ona ściśnięta lub rozciągnięta, tym większa działa siła skierowana w stronę punktu
wyjściowego. Na podstawie dotychczasowych ustaleń możemy stwierdzić ogólnie, że jeżeli funkcje
podaży i popytu są typowe to równowaga rynkowa jest stabilna.
Sprawdźmy, czy tak również będzie w przypadku, gdy jedna z funkcji będzie przebiegała
nietypowo. W punkcie
pisaliśmy o dobrach snobistycznych, na które w pewnym przedziale cen
obowiązuje odwrotna zależność między popytem a ceną, czyli spadek ceny wywołuje spadek popytu.
Na rys. 6 przedstawiono właśnie taką sytuację. Krzywa popytu X jest dla cen z przedziału od p1 do p2
obrazem dobra prestiżowego (efekt Veblena), w stosunku do którego obowiązuje zasada: im wyższa
cena tym większy popyt. Gdyby cena spadła poniżej p1, to wtedy to dobro stało by się dostępne dla
nabywców, którzy nie kierują się tego typu motywacjami przy zakupie i dlatego zaczęłaby obowiązywać
zasada: im niższa cena tym większy popyt. Z kolei, gdy cena wzrośnie powyżej p2 to wtedy z przyczyn
ekonomicznych stanie się to dobro coraz mniej dostępne wraz ze wzrostem ceny i dlatego popyt
stosunkowo szybko zaczyna maleć. Funkcja podaży zaczyna się jednak dla cen wyższych niż p13,
dlatego ten dolny fragment krzywej popytu jest hipotetyczny w tym sensie, że nie zostanie nigdy
zweryfikowany w praktyce.
Tak zazwyczaj jest w przypadku dóbr snobistycznych, że producenci ze względu na duże koszty nie są w stanie zejśc z ceną do
takiego poziomu, aby to dobro stało się powszechnie dostępne.
3
5
Zobaczmy jak w tym przypadku będzie przywracana
równowaga
rynkowa, gdyby ten układ został wytrącony z
X
punktu
równowagi.
Jeżeli cena wzrosłaby powyżej p*, to
p2
wystąpi nadwyżka podaży nad popytem, czyli naturalną
tendencją będzie obniżka cen, co zbliża nas do punktu wyjścia.
Gdyby cena spadła poniżej p*, to z kolei wystąpi nadwyżka
p*
popytu nad podażą, co tworzy impuls do wzrostu cen i tym
samym powrotu do punktu równowagi. Reasumując możemy
powiedzieć, że w tej nietypowej sytuacji wystąpił identyczny jak
p1
poprzednio mechanizm regulacji cen, który przywraca rynek do
punktu równowagi i dlatego ten przypadek należy również
zaliczyć do równowagi stabilnej.
Rozpatrzmy z pozoru bardzo podobny przypadek, który
X
p
Y
prezentuje
rys. 7. Najbardziej widoczna zmiana polega na tym,
X
że
teraz
mamy
dwa punkty przecięcia się funkcji podaży i
X, Y
X*=Y*
p*2
popytu. W typie są one jednak takie jak poprzednio. Zmieniła
Rys. 6.
się jedynie relacja ich wzajemnych nachyleń w okolicach
punktu przecięcia (jak strome są funkcje podaży i popytu).
Zacznijmy od analizy pierwszego punktu równowagi, czyli
oznaczonego na rys.
współrzędnymi p1* i X1*=Y1*. Jeżeli
p*1
cena spadłaby poniżej p1* to wtedy podaż będzie większa niż
popyt i można się spodziewać dalszej obniżki cen, która może
prowadzić do zaprzestania produkcji tego wyrobu. Tym samym
nie stwierdzamy teraz występowania sił rynkowych, które
automatycznie korygowałyby zmiany cen w stronę ceny
równowagi rynkowej. Przyjmijmy jednak dodatkowo, że
X
producenci tego wyrobu wiedzą, że ich wyrób jest dobrem
prestiżowym i mimo nadwyżki podaży nad popytem podnosili
X*1=Y*1 X*2=Y*2 X, Y
ceny, co stopniowo zmniejszało nadprodukcję aż do zera, gdy
ponownie cena ustaliła się na poziomie p1*. Łatwo jednak
Rys. 7.
dostrzec, że posiadając tą wiedzę nadal będą podnosić cenę.
Powstanie wprawdzie wtedy nierównowaga ale dla
producenta jest ona bardzo wygodna, gdyż popyt będzie
większy niż podaż. Taka sytuacja nie skłania producentów do
obniżania cen, gdyż byłoby to sprzeczne z ich interesem. Teraz
mają wymarzoną sytuację. Mogą podnosić cenę i jednocześnie
zwiększać sprzedaż. Możemy więc stwierdzić, że w tej sytuacji
powrót do ceny p1* jest praktycznie niemożliwy. Pierwszy punkt
równowagi jest więc przykładem niestabilnego rozwiązania.
Kontynuując poprzedni wątek rozważań możemy stwierdzić, że stałe podnoszenie cen musi
prędzej czy później doprowadzić do sytuacji, gdy wzrostowi ceny zacznie towarzyszyć spadek popytu.
Podaż z popytem zrównają się ponownie przy cenie p2*, czyli w drugim punkcie równowagi. Jeżeli
stanie się on naszym nowym punktem wyjścia, to na podstawie wcześniejszych ustaleń możemy
powiedzieć, że poniżej ceny p2* istnieją siły rynkowe skłaniające producentów do podwyżek cen, czyli
są to siły kierujące ten rynek w stronę drugiego punktu równowagi. Jeżeli cena rynkowa przekroczyłaby
poziom p2*, to wystąpi nadwyżka podaży nad popytem, co skłania producentów do obniżania cen, czyli
układ samoczynnie powraca do punktu równowagi. Dlatego drugi punkt równowagi jest przykładem
stabilnego rozwiązania.
Na podstawie tych przykładów można sformułować warunek na powstanie stabilnej i
niestabilnej równowagi rynkowej. Jeżeli dla cen wyższch niż cena równowagi rynkowej
występuje nadwyżka podaży nad popytem a dla cen niższych od ceny równowagi jest
odwrotnie, czyli jest nadmiar popytu nad podażą, to taki rynek możemy nazwać stabilnym,
gdyż wytrącony z równowagi będzie do niej samoczynnie powracał.
Równowaga na rynku będzie niestabilna, gdy dla cen wyższych od ceny równowagi
będzie występowała nadwyżka popytu nad podażą albo dla cen niższcy od p* będzie
nadmiar podaży nad popytem. W takim układzie układ wytrącony z punktu równowagi do
niej samoczynnie nie powróci, czego efektem będzie trwała nierównowaga na rynku.
Po prezentacji powyższych rozważań może powstać pytanie, po co się rozważa przypadki
stabilności i niestabilności równowagi rynkowej. Wbrew pozorom ma to praktyczne duże znaczenie,
gdyż realne gospodarki rynkowe są stale niezrównoważone przy czym w niektórych
przypadkach poszukiwanie punktu równowagi przebiega szybko i odchylenia są relatywnie niewielkie.
p
Y
6
Wtedy w uproszczeniu mówimy, że dany rynek jest zrównoważony. W innych przypadkach
dysproporcje między popytem i podażą utrzymują się w dłuższym okresie czasu i są relatywnie duże.
Wtedy mówimy o niezrównoważonym rynku. W realnych gospodarkach równowaga rynkowa jest
najczęściej stanem incydentalnym, do którego dany układ dąży bardziej lub mniej zdecydowanie albo
występuje stała nierównowaga.
Na tym poziomie analizy tylko w ten sposób można wytłumaczyć zjawisko stałej nierównowagi
w warunkach konkurencji doskonałej. Najbardziej spektakularnym przykładem rynków z trwałą
nierównowagą może być rynek luksusowych samochodów niektórych firm, np. mercedes, ferrarii itp.
Na wybrane modele samochodów przyjmuje się zapisy i trzeba czekać po kilka lub nawet kilkanaście
miesięcy, co w rozwiniętych gospodarkach rynkowych jest wyjątkową sytuacją. Producenci ci nie
podnoszą ceny swoich luksusowych wersji do punktu równowagi, gdyż czekająca kolejka dodatkowo
podnosi prestiż ich produktu. Gdyby podnieśli cenę tak aby zrównoważyć rynek, to wprawdzie w
krótkim okresie czasu zwiększyliby zyski ale jednocześnie zmniejszyli efekt prestiżu, co w dłuższej
perspektywie mogłoby się odbić niekorzystnie na cenach i zysku. M.in dlatego świadomie utrzymują
stan nierównowagi na swoje snobistyczne produkty.