Znajdowanie związków miarowych w kwadratach i prostokątach

Kurs e-learningowy
Matematyka – lekcja 35
Opracowanie:
Piotr Kaźmierczyk
35. Znajdowanie związków miarowych w kwadratach i
prostokątach, także z zastosowaniem trygonometrii.
I.
Przypomnij sobie:
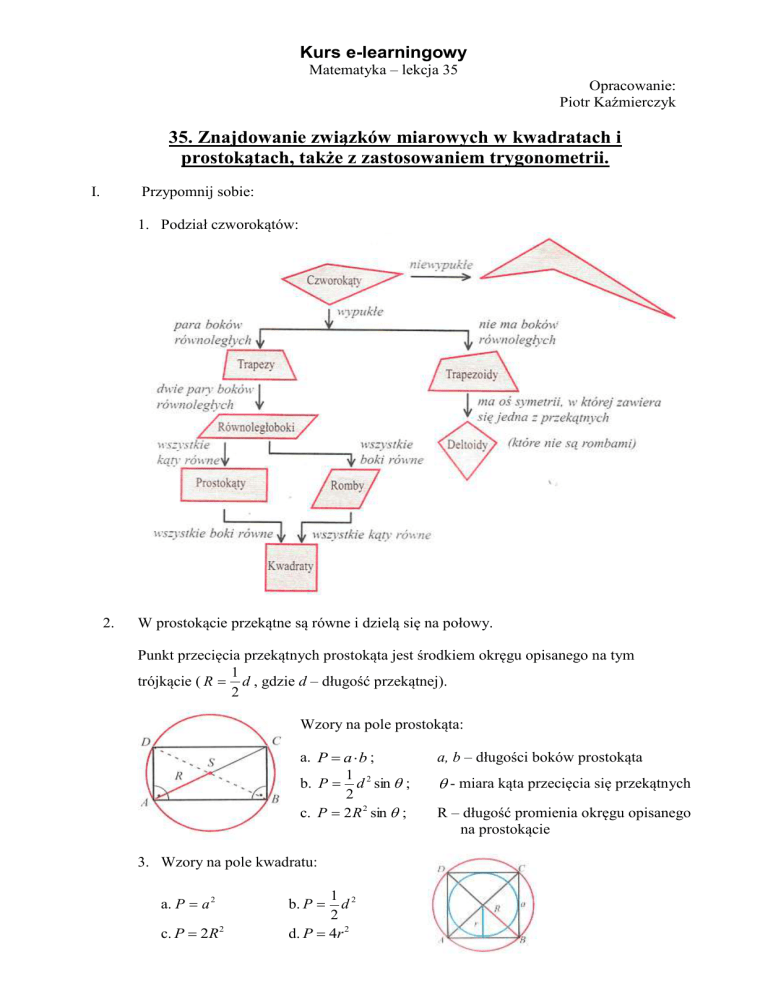
1. Podział czworokątów:
2.
W prostokącie przekątne są równe i dzielą się na połowy.
Punkt przecięcia przekątnych prostokąta jest środkiem okręgu opisanego na tym
1
trójkącie ( R  d , gdzie d – długość przekątnej).
2
Wzory na pole prostokąta:
a. P  a  b ;
a, b – długości boków prostokąta
1
b. P  d 2 sin  ;
 - miara kąta przecięcia się przekątnych
2
c. P  2 R 2 sin  ;
R – długość promienia okręgu opisanego
mmmmmmmmmmmmm na prostokącie
3. Wzory na pole kwadratu:
a. P  a 2
c. P  2R 2
1 2
d
2
d. P  4r 2
b. P 
Kurs e-learningowy
Matematyka – lekcja 35
Opracowanie:
Piotr Kaźmierczyk
W kwadracie przekątne są równe, przecinają się pod kątem prostym i dzielą się na
połowy.
Punkt przecięcia się przekątnych kwadratu jest środkiem okręgu opisanego,
którego promień R jest połową przekątnej kwadratu.
Punkt przecięcia się przekątnych kwadratu jest środkiem okręgu wpisanego,
którego promień r jest połową długości boku kwadratu.
II.
Zobaczmy, jak możemy wykorzystać to w konkretnych przykładach (z
uwzględnieniem czasami nieco innej strategii rozwiązywania zadań zamkniętych i
otwartych).
Przykład 1.
Państwo Kamińscy kupili prostokątną działkę pod budowę domu i ogrodzili ją. Zamówili
metalową bramę o szerokości 5 m i furtkę o szerokości 1 m. Na pozostałą część ogrodzenia
zużyli 122 m siatki. Oblicz:
a. obwód działki L,
b. wymiary działki wiedząc, że stosunek sąsiednich boków działki jest równy 3:5.
Rozwiązanie:
a. Ponieważ na ogrodzenie całej działki użyto 122 m siatki, bramę o szerokości 5 m i furtkę o
szerokości 1 m, to obwód działki wynosi L  122  5  1  128 m.
b. Oznaczmy: a - długość działki;
b - szerokość działki.
Obwód prostokątnej działki (128 m) obliczamy dodając długości wszystkich czterech jej
boków, czyli 128  2a  2b .
Stosunek sąsiednich boków działki jest równy 3:5, czyli b : a  3 : 5 .
Otrzymaliśmy więc układ dwóch równań, który rozwiązujemy:
128  2a  2b / : 2

b 3
 a  5 / 5a
64  a  b

5b  3a
a  b  64 / 3

 3a  5b  0
3a  3b  192

 3a  5b  0
Po dodaniu tych równań stronami otrzymamy 8b  192 , czyli b  24 .
Wstawiając tę wartość do równania a  b  64 otrzymujemy a  24  64 , a następnie a  40 .
Wracając do naszych oznaczeń stwierdzamy:
Odpowiedź: Działka ma długość 40 m i szerokość 24 m. Jej obwód wynosi 128 m.
Kurs e-learningowy
Matematyka – lekcja 35
Opracowanie:
Piotr Kaźmierczyk
Przykład 2.
Do boków kwadratu ABCD dorysowano trójkąt równoboczny CDE oraz kwadrat CBHG.
Wykaż, że trójkąt DGE jest prostokątny.
Rozwiązanie:
Przyjmijmy oznaczenia jak na rysunku obok.
Do wykazania tego, że trójkąt DGE jest prostokątny użyjemy
twierdzenia odwrotnego do twierdzenia Pitagorasa (wzory maturalne
oraz lekcja 28). Bok ED rozważanego trójkąta ma długość a, bok
DG – długość a  a  2a . Natomiast długość boku EG wyliczymy
rozważając trójkąt ECG:
- ponieważ kąt DCE (jako jeden z kątów trójkąta równobocznego) ma miarę 60o, to kąt ECG
(jako przyległy do kąta DCE) ma miarę 180o-60o=120o,
- EC  CG  a , więc trójkąt jest równoramienny; zatem miary kątów przy jego podstawie
są równe i wynoszą: (180o-120o):2 = 60o:2 = 30o,
- gdybyśmy z wierzchołka C poprowadzili wysokość CI na bok EG, to podzieli ona ten bok
1
na połowy, czyli EI  IG  EG ,
2
IG
IG
- w trójkącie prostokątnym CIG mamy: cos CGI 
, czyli cos 30o 
. Zatem
CG
a
3 IG
a 3

 IG 
i ostatecznie EG  2  IG  a 3 .
2
a
2
W trójkącie DEG mamy:
 
ED  EG  a 2  a 3  a 2  3a 2  4a 2  2a   DG
2
2
2
2
2
Odpowiedź: Suma kwadratów długości dwóch boków trójkąta DEG jest równa kwadratowi
długości trzeciego boku, więc jest to trójkąt prostokątny.
Przykład 3.
Kwadrat jest wpisany w okrąg o promieniu 2. Wynika z tego, że obwód kwadratu jest
równy:
A. 4 2 ,
B. 6 2 ,
C. 8 2 ,
D. 10 2 .
Rozwiązanie:
Kwadrat jest wpisany w okrąg, więc jego przekątna jest jednocześnie średnicą okręgu.
Jeśli kwadrat ma boki długości a, to z twierdzenia Pitagorasa mamy a 2  a 2  d 2 , gdzie d
jest długością przekątnej kwadratu (zatem w naszym przypadku d  2  2  4 ).
Obliczamy z tych zależności długość boku a:
Kurs e-learningowy
Matematyka – lekcja 35
Opracowanie:
Piotr Kaźmierczyk
a 2  a 2  4 
2
2a 2  16 2
a  8
2
/:2
2
a  8 2  2 2
Obwód kwadratu o boku a jest równy 4a  4  2 2  8 2 .
Prawidłowa odpowiedź to C.
Przykład 4.
Pole figury wyróżnionej kolorem na rysunku obok jest równe:
A.  2 
3
4
,
B.  2 
3
2
,
C.  2 
2
4
D.  3   2 .
,
Rozwiązanie:
Na rysunku figurę wyróżnioną kolorem otrzymano przez „odcięcie” z każdego z

wierzchołków kwadratu o boku długości  ćwiartki koła o promieniu r  . Pole tej figury
2

 
równe jest zatem różnicy pola kwadratu ( Pkw   ) i pola koła ( Pk  r      
).
2
2
2
2
3
2
Ostatecznie: pole figury z zadania jest równe Pf   
2
3
4
.
Czyli prawidłowa odpowiedź to A.
Przykład 5.
Jeżeli prostokąt A i trójkąt równoramienny B (rysunek obok) mają
równe obwody, to długość odcinka x jest równa:
A. 5,5,
B. 6,
C. 7,5,
D. 11.
Rozwiązanie:
Obwód prostokąta to 2 10  2  5,5  31 , a obwód trójkąta to 2 10  x  20  x . Z równości
obwodów układamy równanie: 31  20  x . Rozwiązujemy je: x  11.
Odpowiedź D.
Kurs e-learningowy
Matematyka – lekcja 35
Opracowanie:
Piotr Kaźmierczyk
ZADANIA DO ROZWIĄZANIA
Zadanie 1. (1 pkt)
Pola dwóch kwadratów różnią się o 16 cm2, a ich boki o 2 cm. Zatem długości boków
wynoszą:
A. 2 i 4 cm,
B. 3 i 5 cm,
C. 4 i 6 cm,
D.5 i 7 cm.
Zadanie 2. (1 pkt)
Długość okręgu wpisanego w kwadrat o przekątnej długości 4 2 wynosi:
A. 2 ,
B. 2 2 ,
C. 4 ,
D. 4 2 .
Zadanie 3. (1 pkt)
W okrąg o środku O i promieniu 6 wpisano kwadrat. Obwód figury wyróżnionej
kolorem na rysunku obok jest równy:
A. 6 2  3 ,
B. 6 2  6 ,
C. 12 2  3 ,
D. 12 2  6 .
Zadanie 4. (2 pkt)
Okno ma kształt prostokąta zakończonego na górze trójkątem równoramiennym
(jak na rysunku). Pole powierzchni okna jest równe 15200 cm2.
a. Jaką wysokość ma część trójkątna okna?
b. Jaką miarę ma kąt przy wierzchołku u szczytu okna?