Znajdowanie związków miarowych w równoległobokach i trapezach

Kurs e-learningowy
Matematyka – lekcja 36
Opracowanie:
Piotr Kaźmierczyk
36.Znajdowanie związków miarowych
w równoległobokach i trapezach,
także z zastosowaniem trygonometrii.
I.
Przypomnij sobie:
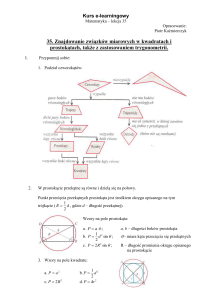
1. Wzory na pola niektórych czworokątów (wzory maturalne):
Mm Trapez
mm P 
ab
h
2
Równoległobok
P  ah  a  b  sin  
ii
Romb
m
P  ah  a 2  sin  
1
 AC  BD  sin 
2
1
 AC  BD
2
2. W równoległoboku przekątne dzielą się na połowy.
3. W rombie przekątne dzielą się na połowy i przecinają się pod kątem prostym.
II.
Zobaczmy, jak możemy wykorzystać to w konkretnych przykładach (z
uwzględnieniem czasami nieco innej strategii rozwiązywania zadań zamkniętych i
otwartych).
Przykład 1.
Różnica długości przekątnych rombu równa jest 2 cm. Wiedząc, że obwód tego rombu ma
długość 116 cm, oblicz długości przekątnych.
Rozwiązanie:
Wprowadźmy oznaczenia:
x– długość dłuższej przekątnej,
x-2 – długość krótszej przekątnej.
Ponieważ (zgodnie z I.3.) w rombie przekątne dzielą się na
połowy i przecinają się pod kątem prostym, to mamy sytuację jak na rysunku.
Kurs e-learningowy
Matematyka – lekcja 36
Opracowanie:
Piotr Kaźmierczyk
2
2
 x  x2
2
Z twierdzenia Pitagorasa dla trójkąta prostokątnego AOD mamy:    
  a (*).
2
2
  

Romb jest czworokątem o bokach równej długości, więc obwód rombu o boku a wynosi 4a.
W naszym przypadku będzie: 4a  116 , czyli a  29 .
2
2
 x  x2
2
Wracając do równania (*) otrzymujemy:    
  29 . Rozwiązujemy:
2  2 
2
2
x
x  4x  4

 841 / 4
4
4
x 2  x 2  4 x  4  3364
2 x 2  4 x  3360  0 / : 2
x 2  2 x  1680  0
2
  b 2  4ac   2  4 1  1680  4  6720  6724
 b     2  82 2  82


 40
2a
2 1
2
bo x (jako długość) powinien być nieujemny
 b     2  82 2  82
x2 


 42 [cm]
2a
2 1
2
x2  2  42  2  40 [cm]
x1 
  6724  82
nie spełnia warunków zadania,
Odpowiedź: Opisany romb ma przekątne długości 42 cm oraz 40 cm.
Przykład 2.
Pole trapezu równoramiennego jest równe 39 3 cm2. Ramię długości 6 3 cm tworzy z
dłuższą podstawą kąt o mierze 30o. Oblicz obwód L trapezu i długość d przekątnej trapezu.
Rozwiązanie:
Rozpatrując trójkąt prostokątny CEB otrzymujemy:
CE
1
h
sin EBC 
, czyli 
, skąd mamy: h  3 3
CB
2 6 3
oraz
EB
3 EB
cos EBC 
, czyli
, stąd EB  9 .

CB
2
6 3
Trapez ABCD jest równoramienny, więc „odcięty” trójkąt CEB jest przystający do „odciętego”
trójkąta A, a więc AF  EB  9 . Zatem a  AB  AF  FE  EB  9  b  9  b  18 .
Pole trapezu P  39 3 , a jednocześnie P 
otrzymujemy:
b  18  b
39 3 
3 3
2
/ :3 3
ab
 h . Wstawiając obliczone wartości
2
Kurs e-learningowy
Matematyka – lekcja 36
Opracowanie:
Piotr Kaźmierczyk
2b  18
2
13  b  9
13 
b4
Czyli a  b  18  4  18  22 , a obwód
L  AB  BC  CD  AD  22  6 3  4  6 3  (26  12 3 ) [cm].
Długość d przekątnej trapezu obliczymy z twierdzenia Pitagorasa dla trójkąta prostokątnego
2
2
AEC: AE  EC  AC
2
 
czyli 9  4   3 3  d 2 . Zatem
2
2
d 2  132  9  3  169  27  196 , więc d  196  14 [cm].
Odpowiedź: Obwód trapezu wynosi L  (26  12 3 ) cm, a długość przekątnej d  14 cm.
Przykład 3.
Obwód figury wyróżnionej kolorem na rysunku obok jest równy:


A. 8 1  5 ,



B. 8 1  3 ,

C. 8 1  3 ,


D. 8 1  5 .
Rozwiązanie:
Figura wyróżniona kolorem jest równoległobokiem o dwóch bokach długości 4 i dwóch
bokach długości d, gdzie d 2  4 2  82 (z tw. Pitagorasa dla białych trójkątów).
d 2  16  64  80 , więc d  80  16  5  4 5 . Zatem obwód
L  2  4  2  4 5  8  8 5  8 1 5


Prawidłowa odpowiedź to D.
Przykład 4.
Stosunek długości ramion trapezu prostokątnego jest równy 2:1. Miara kąta rozwartego tego
trapezu jest:
A. mniejsza od 120o,
B. równa 120o,
C. równa 150o,
D. większa od 150o.
Rozwiązanie:
Na rysunku obok mamy trapez prostokątny a w nim DE  BC . Z warunków zadania wiemy,
AD 2
 , czyli AD  2 BC .
BC
1
Rozpatrujemy trójkąt AED:
DE
BC
1
sin DAE 

 , więc kąt DAE ma miarę 30o.
AD 2 BC 2
że
Kurs e-learningowy
Matematyka – lekcja 36
Opracowanie:
Piotr Kaźmierczyk
Suma miar kątów w czworokącie jest równa 360o ( ABC  BCD  CDA  DAE  360o ),
czyli 90o  90o  CDA  30o  360o . Dalej: CDA  360o  90o  90o  30o  150o
Czyli prawidłowa odpowiedź to C.
Przykład 5.
Pole trapezu ABCD przedstawionego na rysunku obok jest równe:
A.
13
3,
2
B. 39
3
,
2
C. 39,
D. 78.
Rozwiązanie:
W trójkącie AED mamy tg 60o 
P
a  b   h  5  3  5  3
2
Odpowiedź B.
2
3
DE
, czyli
AE
3
13
3
 3 3  39 
2
3
h
3
 h  3 3 . Pole trapezu ABCD:
Kurs e-learningowy
Matematyka – lekcja 36
Opracowanie:
Piotr Kaźmierczyk
ZADANIA DO ROZWIĄZANIA
Zadanie 1. (1 pkt)
Obwód rombu ma długość 48, a promień okręgu wpisanego w ten romb jest równy 3. Kąt
rozwarty tego rombu jest równy:
A. 180o,
B. 150o,
C. 135o,
D. 120o.
Zadanie 2. (1 pkt)
Z wzoru na pole P 
A.
2 P  bh
,
h
ab
h długość podstawy a trapezu określa wyrażenie:
2
B.
2 P  bh
,
h
C.
 2 P  bh
,
h
D.
P  2bh
.
h
Zadanie 3. (1 pkt)
Różnica miar dwóch sąsiednich kątów wewnętrznych równoległoboku jest równa 20o. Kąt
rozwarty tego równoległoboku jest równy:
A. 160o,
B. 140o,
C. 120o,
D. 100o.
Zadanie 4. (2 pkt)
Podstawa trapezu wpisanego w okrąg o promieniu 12 jest średnicą tego okręgu. Kąt ostry
trapezu ma miarę 45o. Oblicz pole P i obwód L tego trapezu.