Kurs e-learningowy
matematyka
Opracowanie:
Piotr Kaźmierczyk
6.Potęgi o wykładnikach wymiernych. Prawa działań na potęgach
o wykładnikach wymiernych i rzeczywistych.
I.
Przypomnij sobie:
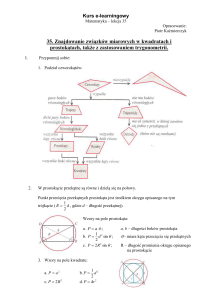
1. Definicję (Wzory maturalne, str.1) potęgi liczby a o wykładniku:
a. naturalnym n: a n a a ... a (n czynników),
1
b. całkowitym: dla a 0 a n n oraz a 0 1 ,
a
m
c. wymiernym: dla a 0 a n n a m ,
dla a 0 a
m
n
1
.
am
2. Definicję pierwiastka (Wzory maturalne, str.1):
Pierwiastkiem arytmetycznym
liczbę b 0 taką, że b n a .
n
n
a stopnia n z liczby a 0 nazywamy
Jeżeli a<0 oraz liczba n jest nieparzysta, to n a oznacza liczbę b<0 taką, że
bn a .
Pierwiastki stopni parzystych z liczb ujemnych nie istnieją.
3. Prawa działań na potęgach (Wzory maturalne, str.1):
Niech r, s będą dowolnymi liczbami rzeczywistymi.
Jeśli a>0 i b>0, to zachodzą równości:
a. a a a
r
s
r s
b. (a ) a
r s
r s
ar
c. s a r s
a
r
ar
a
e. r
b
b
4. Konsekwencją definicji pierwiastka i praw działań na potęgach są między innymi
następujące zależności (wtedy, gdy poniższe pierwiastki są określone):
d. (a b)r a r br
n
a b n a n b
n
a na
b nb
a.
b.
II.
Zobaczmy, jak możemy wykorzystać to w konkretnych przykładach (z
uwzględnieniem czasami nieco innej strategii rozwiązywania zadań zamkniętych i
otwartych).
Kurs e-learningowy
matematyka
Opracowanie:
Piotr Kaźmierczyk
Przykład 1.
Połowa liczby 288 to:
A. 188 ,
B. 244 ,
C. 287 ,
D. 144 .
C. 99 ,
D. 7 7 .
Rozwiązanie:
Obliczamy połowę, czyli
1
liczby 288 :
2
1 88 1 88
2 1 2 21 288 2188 287 .
2
2
Patrz I.1.b.
Zgodnie ze wzorem I.3.a.
Odpowiedź: Wybieramy odpowiedź C.
Przykład 2.
Kwadratem liczby naturalnej jest liczba:
B. 1111 ,
A. 1313 ,
Rozwiązanie:
Podstawami i wykładnikami potęg w powyższym przykładzie są liczby: 13, 11, 9 i 7. Spośród
nich tylko 9 jest liczbą złożoną (na dodatek kwadratem liczby naturalnej 3, czyli 9 = 32= 3 3 ).
Korzystamy ze
wzoru I.3.b.
Jeszcze raz ten
sam wzór I.3.b.
Możemy więc zapisać: 99=(32)9= 329 = 392 =(39)2. Liczba 39 jest oczywiście liczbą naturalną
jako naturalna potęga liczby naturalnej 3 (albo jako iloczyn 3 3 3 3 3 3 3 3 3 ). Zatem 99
jest kwadratem liczby naturalnej 39.
Przekształcenia możemy wykonać też w inny sposób, np.: 99=( 3 3 )9= 39 39 =(39)2.
Odpowiedź: Wybieramy odpowiedź C.
Teraz korzystamy
ze wzoru I.3 d.
Iloczyn takich samych czynników
zapisujemy w postaci potęgi
Przykład 3.
Wyrażenie
A.100,
108 109
zapisane w postaci potęgi liczby 10 to:
11000 105
B.103,
C.106,
D.10-3.
Kurs e-learningowy
matematyka
Opracowanie:
Piotr Kaźmierczyk
Rozwiązanie:
Wzór I.3.a.
Korzystamy z tego, że 109=108+1=108 101 = 108 10 . Przekształcamy licznik naszego
wyrażenia wyłączając wspólny czynnik 108 poza nawias i otrzymujemy:
108 109 108 1 108 10 108 (1 10) 108 11 . Następnie przekształcamy mianownik:
11000 105 111000 105 11103 105 111035 11108 . Wracając do całego wyrażenia
108 109 108 11
mamy:
=
=1=100.
8
5
11000 10 11 10
Bo z I.1.b. wiemy, że a0=1 dla dowolnego a różnego od zera
Odpowiedź: Wybieramy odpowiedź A.
Przykład 4.
5
17
Jeżeli a 3 15 i b 3 4
, to:
8
27
A. a b ,
B. a b ,
C. a b ,
D. a i b są liczbami niewymiernymi.
Rozwiązanie:
Sposób 1:
Jeśli mamy dwie liczby a i b, to musi wystąpić jedna z trzech sytuacji: a<b, a=b, a>b.
Odpowiedź D możemy więc wyeliminować natychmiast w przypadku testu jednokrotnego
wyboru z jakim mamy tu do czynienia.
5
17
Liczby a i b są pierwiastkami 3 stopnia z liczb ujemnych i 15 4 , a jednocześnie
8
27
5
17
15 a 3 i 4
b3 . Łatwo zauważyć, że dla liczb mniejszych od –1 liczby coraz
8
27
5
17
mniejsze mają coraz mniejsze potęgi stopnia nieparzystego. Zatem 3 15 < 3 4
.
8
27
Sposób 2:
Dla liczb a i b wyrażenia podpierwiastkowe zamieniamy na ułamki niewłaściwe a następnie
5
125 3 125 3 125 5
1
a 3 15 3
3
2
8
8
8
2
2
8
stosujemy wzór I.4.b. Otrzymujemy:
17 3 125 3 125 5
2
b 3 4
1
27
27
27
3
3
Czyli a b .
Odpowiedź: Wybieramy odpowiedź C.
Kurs e-learningowy
matematyka
Opracowanie:
Piotr Kaźmierczyk
ZADANIA DO ROZWIĄZANIA
Zadanie 1. (0,5 pkt)
Liczba 4 2 2 w postaci potęgi liczby 2 to:
2
1
2
2
A. 2 ,
3
4
C. 22 ,
B. 2 ,
D. 23 .
Zadanie 2. (0,5 pkt)
Zależność między kilometrem (km) a centymetrem (cm) opisuje równość:
B. 1 cm = 10 –5 km,
A. 1km = 104 cm,
C. 1 cm = 10 –4 km,
D. 1 km = 106 cm.
C. 4,
D. 5.
Zadanie 3. (0,5 pkt)
W przedziale (2; 64) potęg liczby 2 jest:
A. 2,
B. 3,
Zadanie 4. (1,5 pkt)
3
Oblicz: 3 27 9
1, 5
2
1 4 1
.
3 81
Zadanie 5. (2 pkt)
Liczbę 298 3 299 2100 zapisz w postaci potęgi liczby 2.
Wskazówka: Możesz wykorzystać rozumowanie takie jak w przykładzie 3.