m 1 g

I prawo dynamiki
Jeśli cząstka nie oddziałuje z
innymi cząstkami, to można
znaleźć taki inercjalny układ
odniesienia
w
którym
przyspieszenie cząstki jest
równe zeru.
Sir Isaac Newton (1642 - 1727)
(Tlumaczenie z r 1729 Andrew Motte z “Philosophiae Naturalis Principia
Mathematica”:
“Każde ciało pozostaje w spoczynku lub porusza się po linii prostej jeśli nie
działają na nie siły zewnętrzne.’ )
II prawo dynamiki
2
F41
1
4
F43
3

Fwyp 
F42
a


 Fi  ma
i  wszystkie
Fnet
W inercjalnym układzie odniesienia przyspieszenie
cząstki jest proporcjonalne do wypadkowej siły
(sumy sił) działającej na cząstkę i odwrotnie
proporcjonalne do masy cząstki.
III prawo dynamiki


F12  F21
F12
1
F21
2
Akcji towarzyszy reakcja.
Podstawowe oddziaływania
Nicolaus Copernicus
1473-1543
Galileo Gallilei
1564-1642
2
T1
2
T2

3
R1
3
R2
Mm
FG 2
R
Johannes Kepler
1571-1630
Sir Isaac Newton
1642 - 1727
Grawitacja
Na cząstkę o masie m1, oddaloną od cząstki
o masie m2 działa siła przyciągająca ze
strony tej pierwszej:

F21   G m12m 2  r12
r12
1
F21
r12
2
Ciężar
• Rozważmy ciało o masie m


W  mg
W
Na ziemi g = 9.80 m/s2
Na planecie o promieniu R i masie M ciężar ciała jest równy w
przybliżeniu sile grawitacji działającej na to ciało ze strony
planety.

GM
W  m  2 r̂
R
Siła reakcji podłoża
N
Fnet
W
Jest to siła prostopadła do
podłoża, z jaką działa ono
na ciało znajdujące się na
nim.
Przykład: dwie linki i dwie masy na gładkiej
podłodze:
• Dane:T1, m1 i m2 ; ile wynosi a i T2?
T1 - T2 = m1a (a)
T2 = m2a
(b)
dodajemy (a) + (b):
T1
a = m +m
1
2
T1 = (m1 + m2)a
Podstawiamy rozwiązanie do (b):
T2  T1
m2
m1  m2
m2 -T
2
a
T2
m1
T1
i
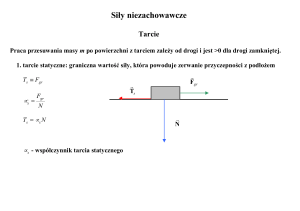
Tarcie statyczne
Siła tarcia statycznego jest to siła styczna
do powierzchni styku dwóch nieruchomych
ciał.
F
N
fs
fs  s N
W
Tarcie kinetyczne
Tarcie kinetyczne jest to siła styczna do
powierzchni dwóch ciał przemieszczających
się względem siebie.
N
f k  k N
fk
f
Fwyp
fs = kN
fs = -Fext
statyczne
kinetyczne
Fext
W
Przykład
Masa m1 = 1.5 kg ciągnięta jest przez linkę z siłą T =
90 N. Tarcie między m1 a m2 :k = 0.51; m2 = 3 kg;
między m2 a stołem nie ma tarcia. Ile wynosi
przyspieszenie a masy m2 ?
(a) a = 0 m/s2 (b) a = 2.5 m/s2 (c) a = 3.0 m/s2
T
a=?
m1
m2
(k=0.51 )
Nie ma tarcia
Rozwiązanie
• Diagram sił dla m1:
N1
T
f = KN1 = Km1g
m1
m1g
Rozwiązanie
• Z III zasady dynamiki Newtona: f12 = - f21

Ale f12 to siła tarcia!
m1
f2,1
m2
f1,2 = Km1g
Rozwiązanie
• Diagram sił dla m2 2:
N2
f2,1 = km1g
m2
m1g
m2g
Rozwiązanie
• Ruch w kierunku poziomym: F = ma
Km1g = m2a
a
1.5 kg
m1
 0.51  9.81 m s 2
k g 
3 kg
m2
a = 2.5 m/s2
f2,1 = Km1g
m2
NAPRĘŻENIE
T
Jak zważyć ziemię?
a ~ M  2r Fg = 2rGm1m2
F= GMZm/R2 = mg
G
/x2
MZ
Henry Cavendish
1731-1810
Pęd
m


p  mv
Pęd jest wielkością opisującą ruch cząstki.
Relacja między energią kinetyczną i pędem
 2


mv 
mv 2
p2
p2

K


2
m
2
2m
2m
v
p
II zasada dynamiki Newtona
W inercjalnym układzie odniesienia:


dp
Fwyp 
dt
klasycznie (nie-relatywistycznie) :





dp dmv 
dv
 ma
Fnet 
m

dt
dt
dt
Energia kinetyczna
Cząstka o masie m, poruszająca się z szybkością v
ma energię kinetyczną
mv 2
K
2
Praca
Praca dW wykonana przez siłę
F
przesuwającą
cząstkę
wzdłuż dr jest równa:
 
dW  F  dr
W postaci całkowej:
F
A
B
dr
jednostka SI pracy
1J = 1N·1m
W
 
 F  dr
droga
Twierdzenie o równoważności pracy i
energii kinetycznej

 mv 2 
dv 
 

  



m
v

d
v
dK  d

m

v
dt

m
a

d
r
 Fwyp  dr  dWwyp

dt
 2 
W inercjalnym układzie odniesienia praca siły wypadkowej działającej na
cząstkę jest równa zmianie energii kinetycznej cząstki
dW = dK
Lub w postaci całkowej: W = K
Przykład
Sanki o masie m stojące na zamarzniętym stawie kopnięto nadając im
prędkość v1. Współczynnik tarcia kinetycznego pomiędzy sankami a
lodem wynosi k. Znajdź odległość jaką przemierzą sanki zanim się
zatrzymają.
Rozwiązanie:
Praca siły tarcia:
W   f k d   k mg
Korzystając z twierdzenia o równoważności pracy i energii kinetycznej:
W  Kk  K p  0  mv / 2
2
1
1
 k mgd   mv12
2
mv12
v12
d 

2 k mg
2k g
Wniosek: droga hamowania nie zależy od masy, jest
proporcjonalna do v2,
Moc
Moc siły jest zdefiniowana jako szybkość z jaką
wykonywana jest przez nią praca.
dW
P( t ) 
dt
Jednostka SI mocy 1W = 1J/1s
t2
Relacja odwrotna:
W   Pt dt
t1
Związek z siłą:
 
P  Fv
Popęd
Jeśli ciało oddziałuje z cząstką w pewnym przedziale
czasowym (t1, t2), to całka
 t2 
I   Ft dt
Jest zwana popędem.
t1
Średnia siła w tym przedziale czasowym jest równa popędowi
dzielonemu przez ten przedział czasowy:
t2 
Fdt

 t1

I
 t  Fav  t
t
Zależność między pędem a popędem
W inercjalnym układzie odniesienia
 t2 
p   Fnet t dt
t1

p2


 t2 

p  pt 2   pt1    dp   Fnet t dt
p1
t1
Przykład
Zmiana pędu:
-wektorowo:
p  mv 2  mv1
-skalarnie:
p  mv2  (mv1 )  m(v2  v1 )
Piłeczka jest:
 t2 
I   Ft dt
t1
Pole pod wykresem tj. popęd
-twarda ( np. golfowa),czas zderzenia t1
-miękka (tenisowa), czas zderzenia t2
FŚR jest ta sama, popęd taki sam ale
Fmax jest większa dla twardej piłki,
bo czas zderzenia jest krótszy.