wykład III - if univ rzeszow pl

Podstawy Fizyki
Wykład 3
Dynamika punktu materialnego
Pęd
Wielkością charakteryzującą ruch ciała jest prędkość. Zmiana ruchu, tzn.
zmiana prędkości, wymaga pokonania oporu bezwładności. Miarą
bezwładności jest masa. Iloczyn masy cząsteczki i jej prędkości nosi
nazwę pędu


p  mv
Pęd jest wielkością wektorową o kierunku
zgodnym z kierunkiem wektora prędkości.
Wektor pędu pełniej charakteryzuje ruch niż
wektor prędkości.

p

v
m
2
Korzystając z definicji prędkości możemy zapisać

dr


p  mv  m
dt
W dowolnym układzie odniesienia pęd możemy rozłożyć na składowe, np. dla
układu kartezjańskiego







p  px ix  p y iy  pz iz  mvx ix  mvy iy  mvz iz
więc
dx
px  m
dt
dy
py  m
dt
p
dz
pz  m
dt
px  p y  pz
2
2
2
3
Zasada bezwładności
(I zasada dynamiki Newtona)
Jeśli cząstka nie oddziałuje
z innymi cząstkami, to można
znaleźć taki inercjalny układ
odniesienia, w którym
przyspieszenie cząstki jest
równe zeru.
Najlepszym przybliżeniem inercjalnego
układu odniesienia jest układ związany
z „gwiazdami stałymi”.
Sir Isaac Newton (1642 - 1727)
4
5
II Zasada dynamiki Newtona
W inercjalnym układzie odniesienia przyspieszenie cząstki jest
proporcjonalne do wypadkowej siły (sumy sił) działającej na
cząstkę i odwrotnie proporcjonalne do masy cząstki.
n
F1
F2
Fwyp
a
Fwyp   Fi  ma
i 1
gdzie n – liczba sił.
Jednostką siły jest niuton (N)
m
m
1N  1kg 1 2  1kg 2
s
s
6
Jeżeli poszukujemy równania opisującegoruch cząstki, czyli
zależności wektora wodzącego od czasu r (t ) , to musimy rozwiązać
równanie:



 dr
d r (t )
m
 F (r , , t )
2
dt
dt
2
Równanie to nazywamy równaniem ruchu Newtona.
Jest ono równoważne trzem równaniom dla poszczególnych składowych.
d 2 x(t )
dx dy dz
m
 Fx ( x, y, z , , , , t )
2
dt
dt dt dt
d 2 y (t )
dx dy dz
m
 Fy ( x, y , z , , , , t )
2
dt
dt dt dt
d 2 z (t )
dx dy dz
m

F
(
x
,
y
,
z
,
, , , t)
z
2
dt
dt dt dt
gdzie




F  Fx ix  Fy iy  Fz iz
 d 2x  d 2 y  d 2z 
a  2 ix  2 i y  2 iz
dt
dt
dt
7
Rozwiązaniem równania ruchu Newtona jest wektor wodzący



 
r  r (t )  x(t )ix  y(t )iy  z(t )iz
Rozwiązanie to zależy od warunków
początkowych,


v
r
a mianowicie od położenia 0 i prędkości 0 cząstki
w chwili początkowej t0


Znajomość siły
 F działającej na cząstkę, oraz położenia r0
i prędkości v0 tej cząstki w chwili t0 pozwala na jednoznaczne znalezienie
funkcji wektora położenia r (t ) , czyli pozwala określić położenie tej
cząsteczki w dowolnej chwili późniejszej (t>t0) lub wcześniejszej (t<t0).
Jest to zasada przyczynowości (determinizmu) mechaniki klasycznej
8
Ogólne równanie ruchu Newtona
Załóżmy, że masa bezwładna cząstki jest wielkością stałą,
czyli m = const. Możemy wtedy równanie ruchu Newtona zapisać:


 

d r (t )
dv (t ) d
dp
m
m
 (mv (t )) 
F
2
dt
dt
dt
dt
2
czyli
 
dp
F
dt
Szybkość zmian pędu ciała jest równa sile zewnętrznej działającej na
cząstkę.
Ostatnie równanie jest ogólniejsze niż poprzednie równanie, gdyż
pozwala opisać ruch ciała o zmiennej masie.
9
Całkując ostatnie równanie w przedziale t = t –t0 , otrzymujemy:

t 
dp
t dt  dt  t F  dt
0
0
t
czyli
t 

 

p  p(t )  p(t0 )   F dt  I
t0

I
nazywamy popędem siły (impulsem siły).
Jednostką popędu siły jest 1 niutonosekunda=1N·1s=1N·s

 p cząstki w przedziale czasu t jest równa
Zmiana pędu
popędowi siły I w tym przedziale czasu
10
Tę samą zmianę pędu możemy osiągnąć albo działając siłą
o małej wartości w dużym przedziale czasu, albo też działając siłą o dużej
wartości w małym przedziale czasu.
Siła o dużej wartości działająca w małym przedziale czasu nazywana jest
siłą impulsową lub zderzeniową.
F
t


p   F dt
t0
t
11
III zasada dynamiki Newtona, Zasada akcji i reakcji
Gdy dwa ciała o masach m1 i m2 oddziałują wzajemnie, to siła F12
wywierana przez ciało drugie na ciało pierwsze jest równa i przeciwnie
skierowana do siły F21, jaką ciało pierwsze działa na drugie




F12   F21  F12  F21  0
12
Jeśli mamy większą liczbę n ciał oddziałujących wzajemnie, to:
n
F
i ,k 1
i k
ik
0
13
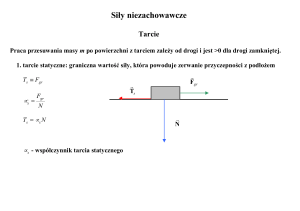
Siła reakcji
Przyczyny ograniczające ruch cząstki nazywamy więzami.
Istnienie więzów powoduje, że w równaniach ruchu należy uwzględnić
dodatkową siłę nazywaną siłą reakcji lub reakcją więzów.
Równanie ruchu cząstki poddanej więzom zapiszemy następująco:


d r (t )   
m
 F (r , v , t )  FR
2
dt
FR
2
Fwyp
Siły reakcji mają kierunek prostopadły do krzywej
lub powierzchni definiującej więzy.
Q
14
Opory ruchu
Przykłady występowania oporów ruchu:
• Klocek przesuwający się po płaskiej powierzchni porusza się z malejącą
prędkością. Jest to przykład tarcia poślizgowego
• Walec toczący się po płaskiej powierzchni także porusza się z malejącą
prędkością. Przykład tarcia tocznego
• Spadanie
pod
wpływem
siły
ciężkości
kulki
metalowej
w cieczy odbywa się ze stałą prędkością. Przykład tarcia wewnętrznego w
ośrodku (lepkości cieczy)
15
Równanie ruchu ciała w przypadku działania oporów ośrodka ma postać:

Siła tarcia FT
  
ma  F  FT

FT
- siła tarcia
jest zawsze skierowana przeciwnie do wektora prędkości ciała


FT   FT iv

 
ma  F  FT iv
gdzie
 v
iv 
v
- wersor o kierunku
i zwrocie prędkości
FT
F
Fn
16
Pełne równanie ruchu wymaga uwzględnienia również siły reakcji więzów

  
ma  F  FT  FR

FR

FR

FT
Tarcie poślizgowe i tarcie toczne
nazywamy tarciem zewnętrznym

F
PRAWA TARCIA
„I prawo tarcia” Siła tarcia między dwoma ciałami jest
proporcjonalna do siły normalnej utrzymującej te ciała w zetknięciu.
FT  FN
W postaci wektorowej:

- współczynnik tarcia


FT  FN iv
17
Interpretacja mikroskopowa tarcia
Tarcie wywołane jest przez oddziaływanie elektromagnetyczne cząstek
stykających się ciał. Powierzchnie nigdy nie są idealnie równe. Na poziomie
mikroskopowym cząstki jednego ciała „blokują drogę” cząstkom drugiego ciała.
Powierzchnia
rzeczywistego
(mikroskopowego)
styku
ciał
jest
w normalnych warunkach wiele rzędów wielkości mniejsza niż powierzchnia
geometryczna
18
„II prawo tarcia” Przy danej sile nacisku FN siła tarcia poślizgowego nie zależy od
wielkości powierzchni zetknięcia między dwoma ciałami.
Wyróżniamy dwa rodzaje współczynników tarcia:
-Współczynnik tarcia statycznego  S - który pomnożony przez siłę nacisku
daje minimalną wartość siły (zwanej siłą tarcia statycznego), którą trzeba
przezwyciężyć, aby wprowadzić w ruch ciało spoczywające na powierzchni.
-Współczynnik tarcia kinetycznego  K - który pomnożony przez siłę nacisku
daje siłę tarcia kinetycznego, czyli siłę którą należy zrównoważyć aby ciało
ślizgające się po powierzchni mogło utrzymać się w ruchu jednostajnym.
Przeważnie
K  S
19
Przykładowe współczynniki tarcia dla wybranych materiałów:
20
„III prawo tarcia” Dla niedużych prędkości współczynnik
kinetycznego nie zależy od prędkości ślizgającego się ciała.
tarcia
Dla dużych prędkości współczynnik tarcia kinetycznego maleje wraz ze
wzrostem prędkości.
21
Tarcie toczne
Poza tarciem statycznym
i kinetycznym (poślizgowym)
wyróżniamy tarcie toczne:

FN 
FT   T
iF
r
Współczynnik tarcia tocznego T
jest zwykle bardzo mały
Przykładowo:
drewno + drewno T = 0,0005 m
stal hartowana + stal T = 0,00001 m
22
Opis ruchu w nieinercjalnym układzie odniesienia
(materiały uzupełniające)
23
Załóżmy, że mamy inercjalny (U) i nieinercjalny (U’) układ odniesienia.
Jeżeli w układzie U’ cząstka P porusza się z przyspieszeniem a’, a układ U’
porusza się względem U z przyspieszeniem a0, to cząstka P w układzie U
porusza się z przyspieszeniem
  
a  a ' a0
Przyspieszenie a0 jest sumą przyspieszenia translacyjnego
i rotacyjnego
 

a0  atr  arot
Rozważmy przypadek, że układy U i U’ poruszają
się względem siebie

ruchem obrotowym z prędkością kątową 
Dla wektorów wodzących punktu P istnieje zależność
 
r  r'
24
Transformacja prędkości między tymi układami ma postać
   
v  v '  r '
Różniczkując po czasie otrzymujemy

  d      
a  a '
 r '2  v '    r '
dt

d


Człon
r'
dt
jest związany z przyspieszeniem kątowym układu U’
 
Wektor 2  v '
Wektor

jest przyspieszeniem Coriolisa
 
    r '
Przyspieszenie
względne układów:
jest przyspieszeniem dośrodkowym

 d      
a0 
 r '2  v '    r '
dt
25
Załóżmy, że obserwator O’ chce zastosować w swoim nieinercjalnym
układzie odniesienia następującą definicje siły
 
ma'  F '
Wykorzystując transformacje przyspieszenia otrzymujemy

 



F '  ma'  ma  ma0  F  FB

F - Siła zmierzona w inercjalnym układzie odniesienia


FB  ma0 - siła bezwładności.
Siła bezwładności nie jest związana z oddziaływaniem otoczenia na cząstkę P. Wiąże
się ona wyłącznie z tym, że układ U’ nie jest układem inercjalnym.
Siła bezwładności jest nazywana siłą pozorną. Uwzględnienie tej siły jest
konieczne jeżeli chcemy stosować zasady dynamiki w układach nieinercjalnych.
26
Siłę bezwładności możemy zapisać


d 

 
  
FB  matr  m
 r '2m  v 'm    r '
dt

  - Siła Coriolisa
FBC  2m  v '

  
2
FBO  m    r '  m r
- Siła odśrodkowa
Ruch ciała możemy opisywać albo w układzie inercjalnym korzystając
z rzeczywistych sił, lub w układzie nieinercjalnym uwzględniając siłę
bezwładności. Oba opisy są prawidłowe. Szczególnie układ nieinercjalny
można dobrać tak, by zagadnienie dynamiczne sprowadzić do problemu
statycznego.
 
F  FB  0
27
Siła bezwładności na Ziemi
Ziemia nie jest inercjalnym układem odniesienia przede wszystkim ze względu
na jej dzienny ruch obrotowy. W układzie związanym z Ziemią występuje zatem
siła bezwładności Coriolisa i odśrodkowa
ma  F  m  (  r )  2m(  v )
Skutkiem działania tych sił są następujące efekty;
1. Zależność przyspieszenia ziemskiego od szerokości geograficznej,
2. Odchylenie kierunku pionu ciała wiszącego nad Ziemią na pewnej wysokości,
3. Wpływ sił Coriolisa na kierunek wiatrów,
4. Obrót płaszczyzny wahań wahadła Foucault,
5. Odchylenie toru przy spadku swobodnym,
6. Przyjęcie przez Ziemię kształtu geoidy.
28
Zależność przyspieszenia ziemskiego od szerokości geograficznej
Siła odśrodkowa jest największa na równiku, a na biegunie wynosi 0.
Wypadkowe przyspieszenie ziemskie będzie równe


     
2
g  g0      R  g0   r

aOd
r
g0
R
aOd
g
g0
g
Wpływ przyspieszenia
odśrodkowego:
 2 r   2 R cos 
m
 (3.34 10 2 ) cos 
s
2
29
Wahadło Foucault'a 1851 r.
Dla obserwatora na Ziemi płaszczyzna ruchu wahadła obraca
się z prędkością kątową
1   sin 
w Warszawie (
 = 52º):
Dla startu z położenia
równowagi
1  12 / h
Dla startu z położenia
maksymalnego wychylenia
30
Odchylenie toru przy spadku swobodnym
31
32