Pole magnetyczne ⇔ prąd elektryczny
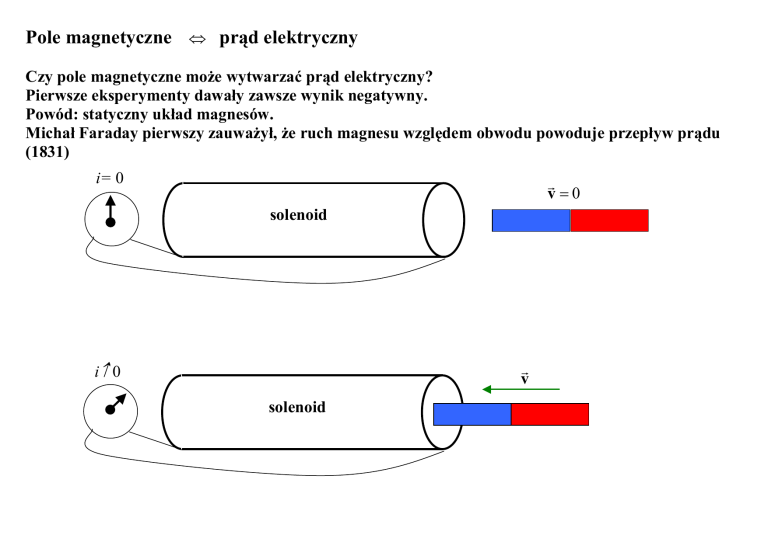
Czy pole magnetyczne może wytwarzać prąd elektryczny?
Pierwsze eksperymenty dawały zawsze wynik negatywny.
Powód: statyczny układ magnesów.
Michał Faraday pierwszy zauważył, że ruch magnesu względem obwodu powoduje przepływ prądu
(1831)
i= 0
r
v=0
solenoid
i≠ 0
r
v
solenoid
Podsumowanie obserwacji: zmiana strumienia pola magnetycznego, przenikającego przez obwód,
powoduje powstanie w tym obwodzie siły elektromotorycznej, a ta – jeżeli obwód jest zamknięty –
powoduje przepływ prądu.
Jest to zjawisko indukcji elektromagnetycznej.
Prawo indukcji Faradaya:
ε = − dΦdt
B
Siła elektromotoryczna indukcji jest równa szybkości zmian strumienia magnetycznego przenikającego
dany obwód, ze znakiem przeciwnym.
Michael Faraday (1791 - 1867)
(źródło: Wikipedia)
Reguła Lenza:
Prąd indukowany ma taki kierunek, że przeciwstawia się zmianie, która go wywołała.
N
N
S
S
N
S
Zastosowanie prawa indukcji Faradaya (w połączeniu z regułą Lenza):
• prądnice elektryczne
• transformatory
• niektóre typy silników
• liczniki prądu elektrycznego
• tygle do topienia metali
Prądy wirowe: prądy indukcyjne powstające w bryłach metalu, w zmiennym polu magnetycznym
• w licznikach, w tyglach – korzystne
• w transformatorach – niekorzystne
Postać całkowa prawa indukcji Faradaya
q0
r
⊗ B
r
B zmienne, rosnące
r
E
ε = − dΦdt
B
W = q0ε
r r
W = ∫ q0 E ⋅ d l
K
ε = ∫ E ⋅ dl
r
K
r r
dΦ B
E
⋅
d
l
=
−
∫
dt
K
r
Magnetyzm materii
Fakt eksperymentalny – w przyrodzie istnieją tylko dipole magnetyczne
Właściwości dipoli magnetycznych:
r
r
1. przyjmują w polu B określony kierunek (|| do B )
r
2. same wytwarzają pole B
µ µ
1
pole dipola B ∝ 3 , w szczególności na osi dipola B = 0 3
2π r
r
gdzie µ 0 - przenikalność magnetyczna próżni
µ - wartość momentu magnetycznego
Przykłady makro: magnesy trwałe, solenoidy, elektromagnesy
Przykłady mikro: niektóre atomy, niektóre cząsteczki, niektóre cząstki elementarne
Związek momentu magnetycznego z momentem pędu
rozważmy ruch orbitalny cząstki naładowanej
µ
r
r
L
r
r
r
r
q
r
v
q
2π r 2
r qvr
2
µ = iS = π r = q
= qω r =
T
T 2
2
2
m
L = mvr
µ
L
=
q
2m
r
v
µ
Jest to zjawisko magnetomechaniczne, a iloraz γ = nazywamy stosunkiem żyromagnetycznym.
L
r r
Widoczne jest, że µ || L , więc
r
r
µ =γ L
Dla dodatnio naładowanej cząstki
e
γ=
2m
Dla ujemnie naładowanej cząstki
e
γ =−
2m
r
Cząstki elementarne mają własny moment pędu, tzw. spin S . Dla niego także
r
r
µ =γ S
ale konieczna jest modyfikacja
γ =g
q
2m
gdzie g jest czynnikiem Landego.
Naturalna jednostka momentu magnetycznego (magneton Bohra)
eh
µB =
= 9,27 ⋅ 10 −24 A m2
2m
1
Dla elektronu S = h , ale g = 2 , więc
2
µS = µB
Moment magnetyczny jest przeciwny do spinu.
Momenty magnetyczne związane z orbitalnym i spinowym momentem pędu są odpowiedzialne za
magnetyzm materii.
Prawa elektromagnetyzmu w obecności magnetyków
Prawo Gaussa jest takie samo:
r r
Φ B = ∫ B ⋅ dS = 0
s
powierzchnia
Gaussa
linie r
pola B
Prawo Ampere’a wymaga modyfikacji
Załóżmy, że wybierzemy jedną z linii pola jako drogę całkowania
r r
∫ B ⋅ dl ≠ 0
K
i=0
r r
B
∫ ⋅ d l ≠ µ 0i
K
droga
całkowania
definiujemy wektor namagnesowania
r
r ∑ µi
M=
V
jest to moment magnetyczny
na jednostkę objętości
A
jednostka namagnesowania 1
m
r r
r r
∫ B ⋅ d l = µ0 ∫ M ⋅ d l
K
K
zgodne z doświadczeniem
Prawo Ampere’a w obecności magnetyków
r r
r r
B
⋅
d
l
=
µ
i
+
µ
M
⋅ dl
0
0∫
∫
K
K
r
Wprowadzamy trzeci wektor magnetyczny H - natężenie pola magnetycznego
r
r
r
B = µ0 H + µ0M
stąd
r r
∫ H ⋅ dl = i
K
jednostka natężenia pola magnetycznego: 1
A
.
m
r
Natężenie pola magnetycznego H pochodzi tylko od prądów makroskopowych;
r
Namagnesowanie M pochodzi od momentów magnetycznych istniejących w materii;
r
Indukcja pola magnetycznego B opisuje w kompletny sposób oddziaływanie pola magnetycznego na
ładunki elektryczne (w ruchu) i na dipole magnetyczne.
W próżni
r
r
B = µ0H
r
r
W materiałach magnetycznych B zależy od H (elektromagnesy)
r
r
B = κ m µ0H
κ m - przenikalność magnetyczna.
r
r
r
r
Zależność B od H bierze się stąd, że pole H wywołuje w materii namagnesowanie M :
r
r
r
B = µ0 H + µ0M
r r
r
µ0 M = B − µ0 H
r
r
r
µ0M = κ m µ0 H − µ0 H
r
r
M = (κ m − 1) H
definiujemy podatność magnetyczną
χ ≡ κm −1
stąd
r
r
M=χH
empiryczna klasyfikacja magnetyków:
diamagnetyki:
κ m nieco < 1,
χ mała i ujemna
paramagnetyki:
κ m nieco > 1,
χ mała i dodatnia
ferromagnetyki: κ m znacznie > 1,
χ duża i dodatnia
Diamagnetyzm
r
zjawisko występowania indukowanego momentu magnetycznego, przeciwnego do pola H .
Można to interpretować jako efekt działania reguły Lenza w skali mikro.
Występuje zawsze, nie zawsze jest widoczny.
Typowa podatność
χ ≈ 10 −6 , niezależna od temperatury.
Przykładowe diamagnetyki: Sb, Bi, gazy szlachetne, H2, benzen, grafit, woda, siarka, sól, kwarc.
Nietypowe diamagnetyki: Cu, Ag, Au.
Test doświadczalny: diamagnetyk jest wypychany z pola magnetycznego w kierunku słabszego pola
r
F
Paramagnetyzm
r
zjawisko występowania indukowanego momentu magnetycznego, zgodnego z polem H .
Wyjaśniamy to istnieniem w niektórych materiałach trwałych momentów magnetycznych.
r
W dielektrykach są to momenty związane z atomami lub cząsteczkami. W zewnętrznym polu H mają
r
one tendencję do ustawienia się || do H . Przeszkadzają temu drgania termiczne. Prawo Curie:
χ=
const
T
słuszne w niskich temperaturach.
Przykładowe paramagnetyki dielektryczne: O2, sole metali przejściowych.
W metalach są swobodne elektrony, które mają spinowy moment magnetyczny. W zewnętrznym polu
r
r
H niewielka ich część ustawia się || do H . Ta podatność jest niezależna od temperatury.
Typowa wartość:
χ ≈ 10 −5
Przykładowe paramagnetyki metaliczne: wszystkie metale, które nie są diamagnetykami, ani
ferromagnetykami.
Test doświadczalny: paramagnetyk jest wciągany w pole magnetyczne w kierunku silniejszego pola
r
F
Ferromagnetyzm
r
zjawisko występowania spontanicznego namagnesowania (nawet w zerowym polu H ).
Wyjaśniamy to istnieniem bardzo silnego sprzężenia między spinowymi (czasem też orbitalnymi)
momentami magnetycznymi elektronów, które mają tendencję do ustawiania się równolegle w jednym
kierunku. Jest to dla nich korzystne energetycznie.
Przykłady: magnetyt Fe3O4, Fe, Co, Ni, Dy, Gd, ich związki i stopy, niektóre stopy pierwiastków
nieferromagnetycznych, np. Cu2MnAl, niektóre tlenki pierwiastków nieferromagnetycznych, np. EuO.
Test doświadczalny:
1. uzyskiwanie bardzo dużego momentu magnetycznego nawet w słabym polu (duża χ )
2. bardzo silne wciąganie w obszar większego pola
r
F
Problem: dlaczego kawałek żelaza na ogół nie jest magnesem, chociaż Fe jest ferromagnetykiem?
Samorzutne uporządkowanie spinowych momentów magnetycznych zachodzi w małych obszarach,
zwanych domenami. Momenty magnetyczne domen skierowane są całkowicie przypadkowo. Ich
suma wektorowa jest równa zeru.
r
H
r
H
r
H
r
H=0
słabe pole
silne pole
pole nasycające
Po wyłączeniu pola stan nasycenia się nie utrzyma, ale pozostanie różne od zera namagnesowanie.
Otrzymamy magnes trwały. Pełny cykl przemagnesowania opisuje pętla histerezy.
M
nasycenie
MR
krzywa magnesowania pierwotnego
- HC
HC
H
- MR
nasycenie
Pętla histerezy
M R - pozostałość magnetyczna (remanencja)
H C - pole koercji
Pole wewnątrz pętli jest miarą pracy na przemagnesowanie (w jednym cyklu).
Zależność namagnesowania od temperatury wewnątrz jednej domeny
M
M max
0
•
•
•
•
•
TC
T
idealne uporządkowanie (maksymalne namagnesowanie) jest możliwe tylko w T=0
ze wzrostem temperatury uporządkowanie zmniejsza się
istnieje temperatura krytyczna TC , w której namagnesowanie spontaniczne spada do zera
powyżej TC ferromagnetyk staje się paramagnetykiem
TC nazywamy temperaturą Curie
Niektóre rodzaje uporządkowania magnetycznego
(rysunki dla T ≈ 0 )
ferromagnetyk
(np. Fe, Co, Ni)
antyferromagnetyk
(np. Cr, FeO)
ferrimagnetyk
(niektóre ferryty,
tj. MO⋅⋅Fe2O3)
Wszystkie mają zastosowanie techniczne: w elektrotechnice, radiotechnice i technice komputerowej.