Etap II

XVII edycja
Międzynarodowego Konkursu Matematycznego
„PIKOMAT”
rok szkolny 2008/2009
Etap II
Klasa IV
Zadanie 1
Z poniższych 5 puzzli z liczbami ułóż kwadrat magiczny, tzn. kwadrat w którym suma liczb
w każdym wierszu, kolumnie i na obu przekątnych jest równa.
6
12
5
8
7
11
4
9
10
Zadanie 2
W kółeczka w wierzchołkach przedstawionej poniżej sześciennej kostki wpisz liczby od 1 do
8 tak, aby sumy liczb na każdej ścianie tej kostki były równe.
Zadanie 3
Kilku przyjaciół postanowiło wspólnie kupić dwuosobowy rower. Gdyby każdy z nich dał po
800 zł, zabraknie 300 zł na zakup roweru. Gdyby zaś każdy z nich dał po 900 zł, to zostanie
300 zł. Ilu było przyjaciół i ile kosztował rower?
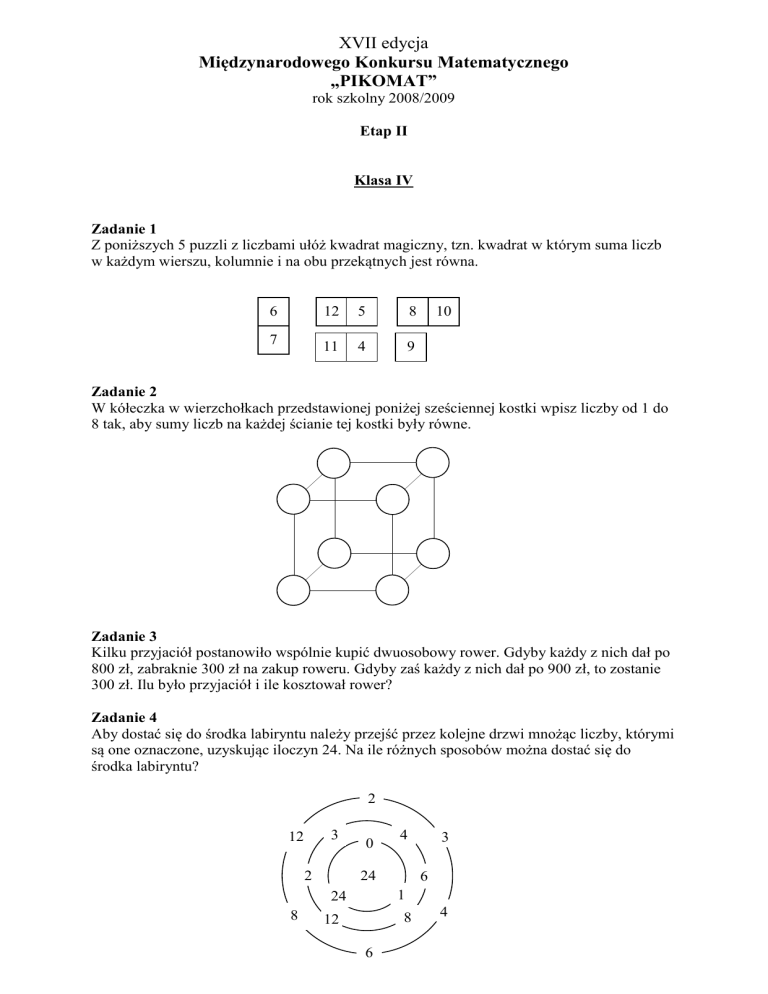
Zadanie 4
Aby dostać się do środka labiryntu należy przejść przez kolejne drzwi mnożąc liczby, którymi
są one oznaczone, uzyskując iloczyn 24. Na ile różnych sposobów można dostać się do
środka labiryntu?
2
3
12
0
24
2
3
6
1
24
8
4
8
12
6
4
Klasa V
Zadanie 1
Zastąp ☼ cyframi od 1 do 9 tak, aby otrzymać prawdziwą równość.
☼ ☼
3
2
☼ ☼
☼
5
☼
+ ☼ ☼ ☼
1
2
3
4
Zadanie 2
Z podanych poniżej elementów ułóż kwadrat 5  5 tak, aby na jego bokach powstały po dwie
takie same liczby pięciocyfrowe, czytane pionowo i poziomo.
1
6
3
2
8
2
6
9
1
2
1
2
9
8
4
7
7
4
5
0
6
4
4
7
3
Zadanie 3
Skarbiec rozbójnika Pikusia pseudonim Dowcipniś jest zabezpieczony dwoma kodowanymi
i zaopatrzonymi w przyciski zamkami. Żeby do niego wejść należy każdy przycisk nacisnąć
odpowiednią liczbę razy. Tylko na niektórych przyciskach napisane jest, ile razy należy je
nacisnąć. Rozbójnik Matuś pseudonim Ciekawski postanowił zaspokoić swoją niesamowitą
wręcz ciekawość i dostać się do skarbca. Żeby zrealizować swój zamiar musi odgadnąć, jakie
liczby zapisane są na poszczególnych przyciskach zamków korzystając z faktu, że niektóre
liczby widnieją na przyciskach oraz, że zdobył pewne instrukcje.
Instrukcja I (dotyczy zamku pierwszego):
Otwierając pierwszy zamek, należy naciskać każdy przycisk tylko
nieparzystą liczbę razy i to tak, aby sumy liczb wyrażających
naciśnięcia na każdym z boków trójkąta były równe.
Instrukcja II (dotyczy zamku drugiego):
Otwierając drugi zamek, można naciskać przyciski tylko 1, 2, 3, 4, 5, 6, 7
lub 8 razy (każdy przycisk naciska się inną liczbę razy) i to tak, aby suma
naciśnięć przycisków leżących na okręgu była o 20 mniejsza od sumy
naciśnięć przycisków leżących na bokach kwadratu.
1
1
5
7
2
Jakie liczby według Ciebie zapisane są na poszczególnych przyciskach zamków?
Zadanie 4
Adaś postanowił kupić prezenty pod choinkę dla swoich rodziców. Dokonał zakupów na
kwotę 105 zł i zapłacił w kasie monetami dwuzłotowymi oraz pięciozłotowymi. Ile monet
pięciozłotowych użył Adaś, jeżeli wiadomo, że kwotę 105 złotych uiścił on w kasie za
pomocą 33 monet?
Klasa VI
Zadanie 1
Uzupełnij puste pola kwadratu liczbami naturalnymi tak, żeby iloczyn liczb w każdym
wierszu, w każdej kolumnie i po obu przekątnych równy był 216.
9
36
18
Zadanie 2
Kwadrat podzielono na 6 jednakowych prostokątów, każdy o obwodzie 28. Oblicz obwód
kwadratu.
Zadnie 3
Oto zanotowane w zeszycie małego Kuby dodawanie, w którym pewne cyfry oznaczone
 uległy zatarciu. Jakie to cyfry?

4
+ 2
1 0
0
3

0
2

0
0
5


0
Zadanie 4
Miasto ma 5 dzielnic. W pierwszej mieszka
3
wszystkich mieszkańców, w drugiej
16
2
4
reszty, w trzeciej
pozostałej reszty liczby mieszkańców, w czwartej 14 tysięcy,
13
11
a w ostatniej o 4 tysiące więcej niż w trzeciej. Ile kg chleba i ile litrów wody mineralnej
należy przygotować dla mieszkańców tego miasta na okres pięciu dni, jeżeli przeciętnie jeden
człowiek zjada dziennie 250 g chleba i wypija 1,5 l wody mineralnej?
Klasa I
Zadanie 1
Naukowiec rozpoczął badania związane z pewnym zagadnieniem, kiedy był w wieku, który
1
równał się
roku jego urodzenia, które ukończył z sukcesem w 2007 roku. W którym roku
30
naukowiec rozpoczął badania i ile miał wtedy lat?
Zadanie 2
Marcin zbudował z18 jednakowych sześciennych kostek prostopadłościan o wysokości trzech
kostek. Ile wynosi pole powierzchni całkowitej zbudowanego przez Marcina
prostopadłościanu, jeżeli wiadomo, że pole powierzchni jednej kostki równe jest 17 cm2?
Zadanie 3
Ośmiu kolegów z klasy: Wojtek, Bartek, Olek, Dawid, Staszek, Kamil, Łukasz i Michał
mieszka w ośmiopiętrowym budynku. Parter tego budynku zajmują sklepy. Na którym piętrze
mieszka każdy z chłopców, jeżeli wiadomo, że:
- Wojtek mieszka na piętrze, którego numer wyraża się liczbą podzielną przez 3;
- Bartek mieszka o 2 piętra wyżej od Wojtka;
- Gdyby Olek przeprowadził się o 3 piętra wyżej, to mieszkałby na tym samym piętrze co
Bartek;
- Dawid nie mieszka na najwyższym piętrze;
- Staszka dzielą dwa piętra od Dawida;
- Kamil mieszka wyżej niż Dawid, ale niżej niż Staszek;
- Łukasz nie korzysta z windy;
- Michał mieszka piętro wyżej niż Staszek.
Zadanie 4
Podczas strasznego sztormu na oceanie uległ zniszczeniu jacht samotnego żeglarza.
Resztkami sił rozbitek dotarł do bezludnej wyspy Pikolandia, która miała kształt trójkąta
równobocznego. Musiał na niej zamieszkać. Postanowił sobie, że codziennie będzie wędrował
na każdy brzeg wyspy, aby sprawdzić, czy nie nadciąga pomoc. W którym miejscu powinien
on wybudować szałas na wyspie, aby suma odległości, które codziennie będzie przebywał,
była najmniejsza?
Klasa II
Zadanie 1
Dana jest pewna liczba trzycyfrowa. Jeżeli dodamy do niej 12 i tę liczbę podzielimy przez 7,
to otrzymamy resztę 5. Jeżeli do danej liczby trzycyfrowej dodamy 14 i zwiększoną liczbę
podzielimy przez 9, znowu otrzymamy resztę 5. Jeżeli do danej liczby trzycyfrowej dodamy
18 i zwiększoną liczbę podzielimy przez 13, także otrzymamy 5. Znajdź daną liczbę
trzycyfrową.
Zadanie 2
Dany jest trójkąt prostokątny, w którym wysokość opuszczona z wierzchołka kąta prostego
1
stanowi
długości przeciwprostokątnej. Znajdź miary kątów ostrych tego trójkąta.
4
Zadanie 3
Masz do dyspozycji 5 żetonów 20 zł, 3 żetony 15 zł, 3 żetony 10 zł, 6 żetonów 5 zł. Rozmieść
je w polach poniższej figury tak, aby suma wartości żetonów wzdłuż każdej zaznaczonej linii
wynosiła 55 zł.
Zadanie 4
Na sześciokącie foremnym o boku 1 opisano okrąg. Następnie wykreślono dwa okręgi,
o środkach w przeciwległych wierzchołkach sześciokąta, o promieniu 1. Oblicz pole
zacieniowanej figury (rys.).
Klasa III
Zadanie 1
Dany jest dowolny czworokąt wypukły. Narysuj pięciokąt wypukły, którego pole jest równe
polu danego czworokąta. Swoją odpowiedź uzasadnij.
Zadanie 2
Kasia zbudowała z brystolu sześcienne pudełko na drobiazgi, bez przykrywki. Wiadomo, że
ścianka tego pudełka ma pole 1 dm2. Rozetnij to pudełko na trzy części tak, aby można złożyć
z nich kwadrat o polu 5 dm2.
Zadanie 3
W pieczarze, przed zamczyskiem, żyje pewien groźny smok o 2000 głów, który prześladuje
niewiasty. Pewnego razu – na wieść o potworze – pojawił się szlachetny, nieustraszony
i wprawiony w walkach ze smokami rycerz, który postanowił zabić smoka. Jednym cięciem
miecza ścina on 33 smocze głowy albo 21 głów, albo 17 głów, albo 1 głowę. Jednakże, gdy
rycerz zetnie smokowi 33 głowy, natychmiast wyrasta mu 48 nowych głów. Gdy rycerz zetnie
17 głów, smokowi odrasta ich 14, gdy zaś rycerz zetnie smokowi jedną głowę, sytuacja jest
wtedy koszmarna – wyrasta mu natychmiast 349 nowych głów. Tylko wtedy, gdy rycerz
zetnie smokowi 21 głów, żadna nie odrasta. Oczywistym jest, że aby zabić smoka, należy
ściąć mu wszystkie głowy. Czy i jak nieustraszony rycerz może zabić smoka?
Zadanie 4
Pan Antoni wygrał w loterii ABA euro. Zwrócił swojemu sąsiadowi dług wartości CBA euro
i pozostało mu BDD euro. Następnie dał swojej ukochanej wnuczce Oli AA euro, a na kupno
płyt z muzyką poważną wydał CA euro i ku jego zdumieniu – pieniądze się skończyły. Jaką
kwotę wygrał w loterii pan Antoni? Wiadomo, że tej samej literze użytej w różnych miejscach
tego zadania odpowiada ta sama cyfra.
Opracowanie: Jan Domaszewicz, Marek Kawałko, Katarzyna Sikora, Katarzyna Żak