Analiza czynnikowa

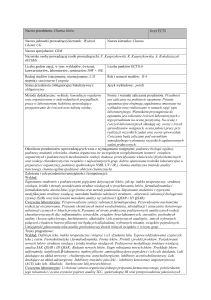
Program przedmiotu
“Opracowywanie danych w chemii”
1.
2.
3.
4.
Wprowadzenie: przegląd rodzajów danych oraz metod
ich opracowywania.
Podstawowe pojęcia rachunku prawdopodobieństwa i
statystyki matematycznej.
Podstawy analizy wyników pomiarów. Statystyczna
weryfikacja hipotez. Analiza wariancji.
Dopasowywanie modeli
a)
b)
c)
d)
e)
5.
6.
Regresja liniowa pojedyncza i wielokrotna.
Regresja nieliniowa.
Analiza konfluentna.
Porównywanie modeli.
Metoda największej entropii.
Analiza skupień: grupowanie podobnych obiektów.
Analiza czynnikowa.
Literatura
•
•
•
•
•
•
J. Czermiński i współautorzy, Metody
statystyczne w doświadczalnictwie
chemicznym. PWN, Warszawa.
S. Brand, Analiza danych, PWN, Warszawa.
A. Strzałkowski, A. Śliżyński, Matematyczne
metody opracowywania wyników pomiarów,
PWN, Warszawa.
C. R. Rao, Modele liniowe statystyki
matematycznej, PWN, Warszawa.
R.G. Brereton, Chemometrics, Wiley.
Sieber,Wild, Nonlinear regression, Wiley.
Pochodzenie danych
• Pomiar (np. pomiary fizykochemiczne)
• Obserwacja (np. zapis zmiany liczebności
populacji na określonym terenie)
• Symulacja (np. symulacje dynamiki
molekularnej ewolucji czasowej zespołów
cząsteczek)
Metody analizy danych
• Analiza statystyczna (obliczanie średnich i
rozrzutu, ocena wiarygodności pomiarów, ocena
istotności różnic wielkości zmierzonych w
różnych miejscach)
• Dopasowywanie modeli matematycznych do
danych pomiarowych (np.analiza regresyjna i
konfluentna)
• Analiza skupień (znajdowanie skupisk obiektów
o podobnych cechach)
• Analiza czynnikowa (wyławianie czynników
określających większość właściwości zbioru
danych lub zjawiska)
Zastosowania
• Analiza statystyczna wyników pomiarów: chemia
analityczna, chemia medyczna, technologia
chemiczna.
• Dopasowywanie modeli: chemia fizyczna,
chemia organiczna, krystalochemia i inne
metody określania struktury cząsteczek, chemia
teoretyczna, technologia chemiczna.
• Analiza skupień: analiza konformacyjna, QSAR.
• Analiza czynnikowa: QSAR, spektroskopia.
Rachunek prawdopodobieństwa
A – zdarzenie
E – przestrzeń wszystkich zdarzeń
P(A) – prawdopowobieństwo zdarzenia A;
liczba nieujemna określająca częstość
jego występowania.
P(E)=1
P(A+B)=P(A)+P(B) dla zdarzeń
wykluczających się.
Prawdopodobieństwo warunkowe i
niezależność zdarzeń
P(A|B)=P(AB)/P(B)
P(AB)=P(A|B)P(B)
Zdarzenia A i B są niezależne jeżeli
P(A|B)=P(A)
czyli
P(AB)=P(A)P(B)
Zmienne losowe i ich rozkłady
Zmienna losowa: liczba przyporządkowana
zdarzeniu
Dystrybuanta:
F(x)=P(yx)
Gęstość prawdopodobieństwa:
f(x)=dP(x)/dx
Funkcja zmiennej losowej jest też zmienną
losową.
Dystrybuanta liczby oczek na jednej ścianie kostki dla rzutów idealnie
symetryczną kostką.
1
F(x)
0.5
1
2
3
4
5
6
x
Momenty rozkładu
Dla zmiennych ciągłych:
n
E ({x})   x i Px  x i 
E{x}  x̂ 
i 1

 xf x dx

n

i 1

EH ( x )   H x i Px  x i  EHx    Hx f x dx
Jeżeli H(x)=(x-xc)n to E{H(X)} nazywa się n-tym
momentem x względem c; jeżeli c= x̂ to E jest n-tym
momentem centralnym, mn({x}).
Użyteczne momenty centralne
Wariancja


2
x  m 2 x   x  x̂  f x dx
2

Skrzywienie
m 3 x
1
3
x  x̂  f x dx
 x  3 / 2
 3

m 2 x  x 

Kurtoza
m 4 x
1
4
x  x̂  f x dx  3
x  2
3  4

m 2 x
 x 

Obliczanie momentów centralnych
zbioru punktów
1 n
x̂   x i
n i 1
2
n
n

1
1 

 
2
2
2
x i  x̂  
 
n xi    xi 

n  1 i 1
n  1  i 1
 i 1  
n
n

 x
i 1
i
(n  1)3
n

 x̂ 
3
 x
i 1
 x̂ 
4
i
(n  1)
4
3
Przykłady momentów centralnych
paru rozkładów
Wartość najbardziej prawdopodobna (modalna): xm: f’(xm)=0, f’’(xm)<0
Mediana: x0.5: P(x<x0.5)=0.5
Wartość średnia:
x

 xf x dx

f(x)
xm x0.5 x
x
Mediana i kwantyle
F(x)
1.0
xq
Fx q    f x dx  q
0.5

0.2
x0.2
x0.5
mediana
x0.9
x
Rozkład dwóch zmiennych i
kowariancja
10  Ex   x̂
 01  Ey   ŷ


 E y  ŷ     y 
m 20  E x  x̂    2 x 
2
m 02
2
2
m11  Ex  x̂ y  ŷ   covx , y 
covx , y 
x , y  
x y 
Sposoby przedstawiania rozkładów zmiennych
losowych:
1. Wykresy liniowe (rozkłady jednowymiarowe).
2. Wykresy „rozproszone” (scatter plots) (dwuwymiarowe)
3. Histogramy
Rozkład normalny
f x ; m ,   
 x  m 2 
1

exp  
2

2

2 


 x2 
1
f u;1,0  
exp   
2
 2 
 x  m  
Fx; m,    erf 

  
U = zmienna stadardyzowana
Wielowymiarowy rozkład normalny

det( A)
 1  T  
f ( x1 , x 2 ,..., x n )  f (x ) 
exp  x  m  Ax  m
n/2
2
 2

Centralne twierdzenie graniczne
Jeżeli x jest zmienną losową o wartości średniej a
i wariancji b2, to zmienna
n
1
  lim n   x i
n
i 1
Ma rozkład normalny o wartości średniej a i
wariancji b2/n.