ĆWICZENIE 2

ĆWICZENIE 6
POMIARY REZYSTANCJI
I. Cel ćwiczenia
Celem ćwiczenia jest wdrożenie umiejętności poprawnego wyboru metody
pomiaru w zależności od wartości mierzonej rezystancji oraz postulowanej
dokładności wyniku pomiaru. Wybór dotyczy: omomierza cyfrowego, metody
technicznej, mostka Wheatstone’a i mostka Thomsona.
II. Zagadnienia
1. Zasada pomiaru rezystancji omomierzem cyfrowym.
2. Metoda techniczna pomiaru rezystancji.
3. Zasada pomiaru rezystancji mostkiem Wheatstone’a i Thomsona.
4. Konstrukcja technicznego i laboratoryjnego mostka Wheatstone’a.
5. Układ technicznego i laboratoryjnego mostka Thomsona.
6. Warunek równowagi mostka Wheatstone’a i Thomsona.
III. Wprowadzenie
Wybór metody pomiaru rezystancji zależy od jej wartości, charakterystyki
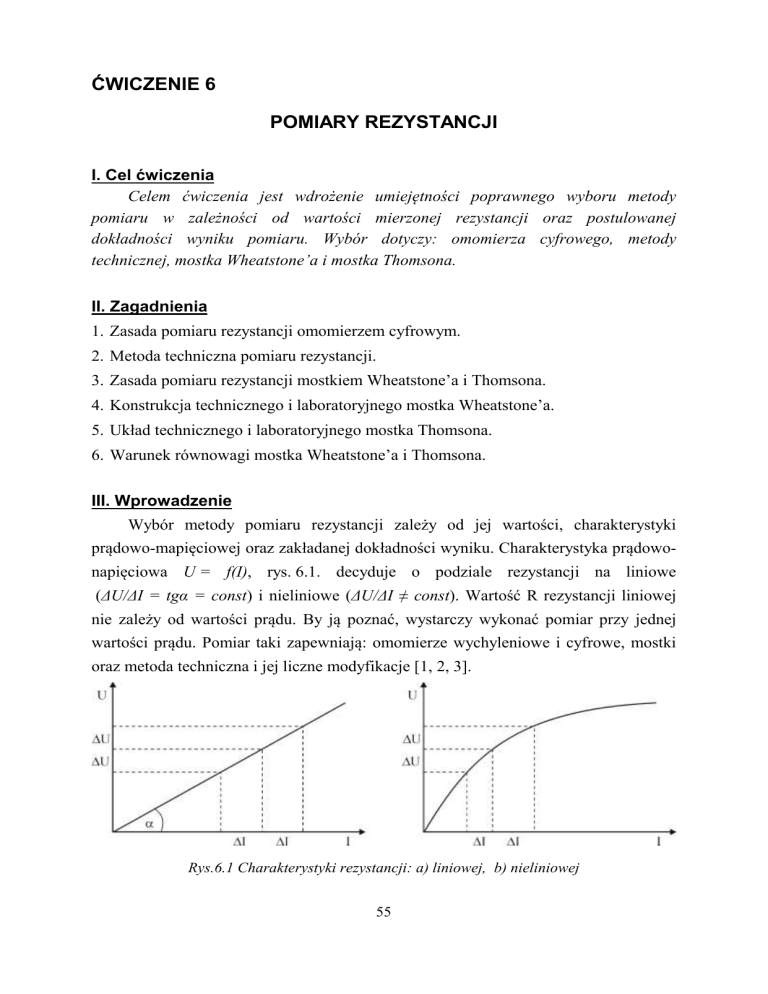
prądowo-mapięciowej oraz zakładanej dokładności wyniku. Charakterystyka prądowonapięciowa U = f(I), rys. 6.1. decyduje o podziale rezystancji na liniowe
(ΔU/ΔI = tgα = const) i nieliniowe (ΔU/ΔI ≠ const). Wartość R rezystancji liniowej
nie zależy od wartości prądu. By ją poznać, wystarczy wykonać pomiar przy jednej
wartości prądu. Pomiar taki zapewniają: omomierze wychyleniowe i cyfrowe, mostki
oraz metoda techniczna i jej liczne modyfikacje [1, 2, 3].
Rys.6.1 Charakterystyki rezystancji: a) liniowej, b) nieliniowej
55
Do pomiaru rezystancji nieliniowych, które zmieniają wartość w zależności od
wartości prądu przez nie płynących, układ pomiarowy powinien zapewnić kontrolę
wartości prądu i napięcia na rezystancji mierzonej. Wymaganie takie spełnia metoda
pośrednia zwana techniczną.
1. Pomiary rezystancji liniowych
Praktyczne pomiary rezystancji obejmują wartości w zakresie od 10-6 Ω
(rezystancja przewodów, boczników) do 1014Ω (rezystancja izolacji), zaś wymagania
co do dokładności zmieniają się w granicach od 10-4 % (pomiary wzorców rezystancji)
do kilku procent (pomiary techniczne).
1.1. Omomierze
Do pomiarów rezystancji o wartościach z zakresu 1Ω  200Ω służą omomierze
analogowe równoległe, dla wartości z zakresu 10Ω –10MΩ omomierze szeregowe, zaś
omomierze elektroniczne o różnych zakresach mierzą do wartości 1010Ω. Omomierze
elektroniczne
cyfrowe
działają
wykorzystując
przetworzenie
rezystancji
na
proporcjonalne do niej napięcie i następnie cyfrowy pomiar napięcia. Często stanowią
jedną z funkcji multimetru cyfrowego (DMM – Digital MultiMeter). Omomierze
cyfrowe o dużej rozdzielczości zapewniają dokładność pomiaru rzędu 0,05%
1.2. Metoda zerowa
Do pomiarów o średniej dokładności (około 1%) służą mostki techniczne.
Techniczne mostki Thomsona mierzą rezystancje w zakresie od 10-4Ω do 1Ω.
Techniczne mostki Wheatstone’a mają zakres pomiarowy 1Ω – 100kΩ. Laboratoryjne
mostki Wheatstone’a zapewniają pomiar dokładny, rzędu 0,05 %.
Rys.6.2. Schemat laboratoryjnych mostków a) Wheatstone’a b) Thomsona
56
Zrównoważony mostek czteroramienny Wheatstone’a (rys. 6.2.) realizuje metodę
zerową pomiaru rezystancji. W mostku rozróżnić można przekątną zasilania AB
i przekątną wskaźnika zera (galwanometru) CD. Zazwyczaj przyjmuje się, że
rezystancja mierzona wpinana jest do gałęzi mostka w miejsce R1, czyli Rx = R1.
Regulując odpowiednio rezystancje R2, R3, R4 (rezystancje w ramionach mostka) należy
zrównoważyć mostek, czyli doprowadzić do wartości zerowej prąd galwanometru:
Ig = 0. W stanie równowagi obowiązuje zależność zwana warunkiem równowagi:
(6.1)
Rx R4  R2 R3
Mierzoną rezystancję można wyznaczyć z wyrażenia:
R R
Rx  2 3
R4
Jeżeli R2, R3 i R4
(6.2)
są rezystorami wzorcowymi, to mierzona rezystancja Rx jest
porównywana bezpośrednio z wzorcami i dokładność pomiaru zależy od ich
dokładności:
Rx  R2  R3  R4 
(6.3)
Praktycznie równoważenie mostka odbywa się na dwa sposoby:
-
przez zmianę R2 (tzw. rezystancji porównawczej) przy dobranym wcześniej
stosunku R3/R4 = const, ten sposób stosowany jest w mostkach laboratoryjnych,
-
przez zmianę stosunku R3/R4 przy utrzymaniu R2 = const, ten sposób stosowany
w mostkach technicznych.
Mostek Thomsona (sześcioramienny) służy do pomiaru rezystancji o małych
wartościach, ponieważ jego konstrukcja umożliwia eliminację wpływu rezystancji
przewodów łączących i styków na wynik pomiaru. Jeżeli dla mostka Thomsona
spełniony zostanie dodatkowy warunek:
R3' R4'

R3 R4
(6.4)
to równanie na jego warunek równowagi przyjmuje postać taką samą, jak dla mostka
Wheatstone’a i Rx można wyznaczyć ze wzoru:
R R
Rx  N 3
R4
(6.5)
1.3. Metoda porównawcza i podstawienia
Metoda porównawcza należy do dokładnych metod pomiaru rezystancji a polega
na porównaniu za pomocą kompensatora spadków napięcia na połączonych szeregowo
(rys. 6.3.) rezystorze wzorcowym Rw i rezystorze badanym Rx (zakres stosowania:
57
10-4 - 1013 Ω). Dzięki zastosowaniu kompensatora napięcia można przyjąć, że przez
rezystor badany i rezystor wzorcowy płynie ten sam prąd. Wtedy, z pomiarów:
U w  I  Rw oraz
U x  I  Rx
można otrzymać:
R U
Rx  w x
Uw
(6.6)
(6.7)
Rys.6.3 Zasada pomiaru rezystancji metodą porównania
Dokładność metody porównawczej określa wzór:
Rx   Rw  U x  U w 
(6.8)
Metoda podstawienia (rys. 6.4.) zapewnia dokładny pomiar rezystancji o dużej
wartości (zakres stosowania: 104 - 1012 Ω). Polega ona na podstawieniu w obwodzie
z czułym wskaźnikiem prądu w miejsce mierzonej rezystancji – rezystancji wzorcowej
o regulowanej wartości. Należy tak nastawić tę rezystancję, by po jej podstawieniu
wskaźnik prądu nie zmienił swego wskazania. Wtedy:
I Rx = I Rw = U
(6.9)
Zatem:
Rx = R w
oraz:
δRx = ± |δRw |
Rys.6.4 Zasada pomiaru rezystancji metodą podstawienia
58
(6.10)
(6.11)
2. Pomiar rezystancji nieliniowych (metoda techniczna)
Do pomiaru rezystancji nieliniowej (ale można nią mierzyć również rezystancje
liniowe) służy metoda techniczna, pośrednia, polegająca na wykorzystaniu
woltomierza i amperomierza (rys. 6.5). Wartość mierzonej rezystancji Rx wylicza się na
podstawie prawa Ohma ze wskazań przyrządów. Obliczona wartość Rx obarczona jest
błędem systematycznym wynikającym z niedoskonałości energetycznej woltomierza
lub amperomierza (pobór prądu IV przez woltomierz, albo spadek napięcia UA na
amperomierzu).
Rys. 6.5 Układy do pomiaru rezystancji metodą techniczną:
a) poprawnie mierzonego prądu, b) poprawnie mierzonego napięcia
a) Układ poprawnie mierzonego prądu (amperomierz wskazuje prąd płynący
przez Rx)
Poprawną wartość rezystancji Rx określa wzór:
U
U  U A UV
Rx  x  V

 RA
Ix
Ix
Ix
(6.12)
gdzie: Ux jest napięciem na rezystancji Rx, UV jest wskazaniem woltomierza (Ux + UA),
UA napięciem na amperomierzu, Ix wskazaniem amperomierza
Błąd metody wynosi:
ΔRx = +RA
(6.13)
Wynika stąd wniosek, by układ poprawnie mierzonego prądu stosować do pomiaru
rezystancji o dużych wartościach (Rx >> RA) .
b) Układ poprawnie mierzonego napięcia (woltomierz wskazuje spadek napięcia
na Rx)
Poprawną wartość rezystancji Rx określa wzór:
U
Ux
Rx  x 
I x I A  IV
59
(6.14)
gdzie: Ux jest wskazanie woltomierza (UV = Ux), IA jest wskazaniem amperomierza
(IA = Ix + IV ), a IV jest to prąd pobierany przez woltomierz
Błąd metody wynosi:
Rx  
Rx
R
1 V
Rx
(6.15)
Wynika stąd wniosek, by układ poprawnie mierzonego napięcia stosować do
pomiaru rezystancji o małych wartościach (Rx << RV).
Dla ułatwienia decyzji, jeżeli dostępne są dane techniczne woltomierza i amperomierza
i można z nich uzyskać wartości RV i RA na wykorzystywanym zakresie, oblicza się
rezystancję graniczną Rg ze wzoru:
Rg  RV  RA
(6.16)
Dla Rx < Rg stosuje się układ poprawnie mierzonego napięcia.
Dla Rx > Rg stosuje się układ poprawnie mierzonego prądu.
Określenie dokładności metody technicznej powinno uwzględniać błąd metody
wybranego układu (który jako błąd systematyczny może być wyeliminowany za
pomocą poprawki) oraz błędy graniczne wnoszone przez woltomierz i amperomierz
a zależne od ich klasy. Dla metody pośredniej błąd względny graniczny wynosi:
δRx = ± (|δU|+ |δI|)
(6.17)
Praktycznie dokładność metody technicznej wynosi ok. ±1  5%.
IV. Program ćwiczenia
1. Wybrać rezystor z zestawu, zapisać jego dane do tabelki. Dobrać zakres pomiarowy
omomierza na podstawie przewidywanej wartości rezystancji rezystora wynikającej
z jego danych. Zweryfikować zakres, by błąd rozdzielczości pomiaru był
najmniejszy. Zanotować wynik i obliczyć bezwzględną wartość błędu granicznego
pomiaru.
2. Zmierzyć rezystancję tego samego rezystora metodą techniczną. Zapisać w tabelce
dane zastosowanych przyrządów. Obliczyć przewidywane wartości napięcia i prądu
(należy założyć jedną z nich np. równą zakresowi woltomierza ale mniejszą lub
równą napięciu osiąganemu z zasilacza). Zestawić w tabelce dobrane zakresy
pomiarowe oraz podać charakterystyczne dla nich rezystancje wewnętrzne. Obliczyć
rezystancję graniczną Rg dla dobranych zakresów pomiarowych i dokonać wyboru
60
metody pomiaru (poprawny pomiar napięcia albo prądu). Obliczyć błędy
systematyczne metody. Zmontować wybrany układ pomiarowy, zapisać wyniki
i dokonać potrzebnych obliczeń.
3. Wybrać rezystor z zestawu i podłączyć do mostka. Ustawić na technicznym mostku
Wheatstone’a przewidywany zakres pomiarowy. Zrównoważyć mostek. Odczytać
i zapisać wartość mierzonej rezystancji (Rx). Powtórzyć pomiary w celu
wyeliminowania powstania błędu grubego. Określić i obliczyć wartość błędu
granicznego względnego (Rx) i bezwzględnego (Rx) pomiaru. Zapisać wynik
pomiaru.
4. Za pomocą technicznego mostka Thomsona zmierzyć wybraną rezystancję. W celu
eliminacji błędu grubego powtórzyć dodatkowo pomiar.
V. Pytania kontrolne
1. Podaj i omów wzór na błąd graniczny pomiaru rezystancji omomierzem cyfrowym.
2. Narysuj układ do pomiaru rezystancji metodą techniczną.
3. Podaj zasadę pozwalającą wybrać układ pomiarowy, wprowadzający mniejszy
błąd systematyczny w technicznej metodzie pomiaru rezystancji.
4. W jakim celu zmieniamy kierunek prądu w obwodzie mostka (tzw. komutacja)?
5. Co ogranicza zakres pomiarowy mostka Wheatstone’a od dołu a co od góry?
7. Różnice budowy mostka czteroramiennego (Wheatstone’a) i sześcioramiennego
(Thomsona). W jakim celu skonstruowano mostek sześcioramienny.
8. Schemat i rozwiązania konstrukcyjne mostka technicznego Thomsona.
Literatura
1. Chwaleba A.: Metrologia elektryczna, Warszawa: WNT, 1997.
2. Dyszyński J.: Metrologia elektryczna i elektroniczna - laboratorium cz.I, Rzeszów:
Wydawnictwo PRz, 1997.
3. Marcyniuk A., Pasecki E.,Pluciński M., Szadkowski B, Podstawy metrologii
elektrycznej, WNT, Warszawa 1984
4. Szadkowski B. (red) Laboratorium metrologii elektrycznej i elektronicznej, Wyd.
Polit. Śląskiej, Gliwice, 1998
61