Zadania do rozdziału 7.
Zad.7.1.
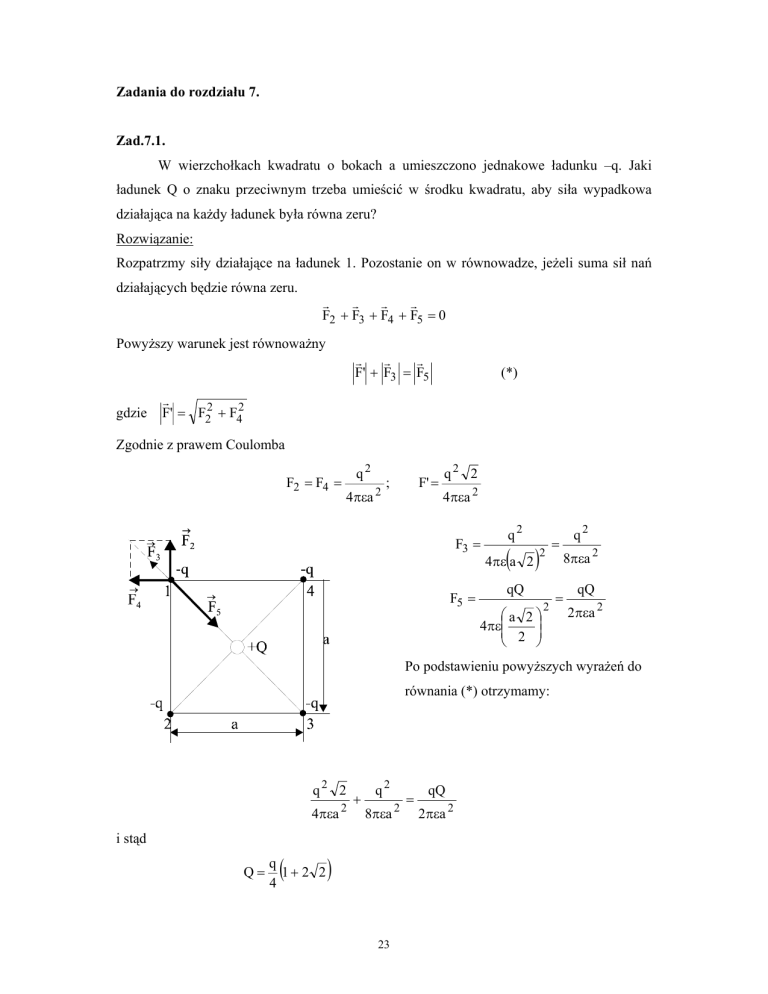
W wierzchołkach kwadratu o bokach a umieszczono jednakowe ładunku –q. Jaki
ładunek Q o znaku przeciwnym trzeba umieścić w środku kwadratu, aby siła wypadkowa
działająca na każdy ładunek była równa zeru?
Rozwiązanie:
Rozpatrzmy siły działające na ładunek 1. Pozostanie on w równowadze, jeżeli suma sił nań
działających będzie równa zeru.
G
G
G
G
F2 + F3 + F4 + F5 = 0
Powyższy warunek jest równoważny
G
G
G
F' + F3 = F5
gdzie
(*)
G
F' = F22 + F42
Zgodnie z prawem Coulomba
F2 = F4 =
q2
4πεa 2
F' =
;
q2 2
4πεa 2
F3 =
F5 =
q2
( )2
=
4πε a 2
qQ
a 2
4πε
2
2
=
q2
8πεa 2
qQ
2πεa 2
Po podstawieniu powyższych wyrażeń do
równania (*) otrzymamy:
q2 2
4πεa
2
+
q2
8πεa
i stąd
Q=
(
q
1+ 2 2
4
)
23
2
=
qQ
2πεa 2
Taki sam tok rozumowania można zastosować dla każdego ładunku Q umieszczonego w
pozostałych wierzchołkach kwadratu.
Zad.7.2.
Cztery jednakowe ładunki q umieszczono w narożach kwadratu o bokach a. Znaleźć
natężenie i potencjał pola elektrycznego w środku kwadratu?
Rozwiązanie:
G
Natężenie pola elektrycznego E w środku
kwadratu wynosi:
G G
G
G
G
E = E1 + E 2 + E 3 + E 4 , gdzie:
G
q⋅4
q
1 Q1
1
E1 = E1 =
=
⋅
=
2
2
4πε r
4πε a ⋅ 2 2πεa 2
1
G
q⋅4
q
1
1 Q2
E2 = E2 =
=
⋅
=
2
2
4πε a ⋅ 2 2πεa 2
4πε r
2
G
q
1 Q3
1 q⋅4
E3 = E3 =
=
⋅
=
2
2
4πε r
4πε a ⋅ 2 2πεa 2
3
G
q
1 Q4
1 q⋅4
E4 = E4 =
=
⋅
=
4πε r 2
4πε a 2 ⋅ 2 2πεa 2
4
Widzimy, że E1 = E 2 = E 3 = E 4 .
Z geometrii układu ładunków wynika, że
G
G
G
G
E1 = − E 3 i E 4 = −E 2 ,
G
Zatem natężenie pola E w środku kwadratu wynosi:
G G
G
G
G
E = E1 + E 2 + E 3 + E 4 = 0
Potencjał V pola elektrycznego w środku kwadratu wynosi:
V = V1 + V2 + V3 + V4 , gdzie:
V1 =
1 Q1
1 q⋅2 q 2
⋅
=
=
4πε r1 4πε a 2 4πεa
V2 =
1 Q2
1 q⋅2 q 2
=
⋅
=
4πε r2
4πε a 2 4πεa
V3 =
1 Q3
1 q⋅2 q 2
⋅
=
=
4πε r3
4πε a 2 4πεa
24
V4 =
1 Q4
1 q⋅2 q 2
⋅
=
=
4πε r4
4πε a 2 4πεa
Widzimy, że V1 = V2 = V3 = V4 .
Potencjał V pola elektrycznego w środku kwadratu wynosi
V = V1 + V2 + V3 + V4 = 4
q 2 q 2
=
4πεa πεa
Zad.7.3.
Obliczyć potencjał pola elektrycznego w punkcie o współrzędnych (x,y), dla układu
trzech
ładunków:
Q1 = q , Q 2 = 2 2 q , Q 3 = − q
umieszczonych
w
punktach
o
współrzędnych: Q1 (0, a ), Q 2 (0,0), Q 3 (a ,0) . Wyznaczyć V dla punktu P(a,a).
Rozwiązanie:
Całkowity potencjał pola elektrycznego V(x,y) w dowolnym punkcie P(x,y), można
przedstawić jako sumę potencjałów V(r1 ), V(r2 ) i V(r3 ) wytworzonych w tym punkcie przez
każdy z ładunków z osobna
V(x , y ) = V(r1 ) + V(r2 ) + V(r3 )
V(r1 ) =
1 Q1
1 q
=
4πε r1 4πε r1
V(r2 ) =
1 Q2
1 2 2q
=
4πε r2
4πε r2
V(r3 ) =
1 Q3
1 q
=−
4πε r3
4πε r3
25
Ale
r1 = x 2 + (y − a )2
r2 = x 2 + y 2
r3 =
(x − a ) 2 + y 2
Zatem
V(x , y ) =
q
1
+
4πε x 2 + (y − a )2
2 2
x 2 + y2
−
2
(x − a ) + y 2
1
Potencjał w punkcie P(a,a) wynosi
V(a , a ) =
q 1 2 2 1
+
−
4πε a a 2 a
V(a , a ) =
q
2πεa
Zad.7.4.
Obliczyć natężenie pola elektrycznego w otoczeniu tzw. dipola elektrycznego, tj.
układu dwóch różnoimiennych, jednakowych co do wartości ładunków elektrycznych
+Q i –Q, rozsuniętych na odległość a, biorąc pod uwagę tylko punkty leżące na osi dipola
(patrz rysunek).
Rozwiązanie:
-Q
0
+Q
E_
A
E+
oś dipola
a
r
Weźmy pod uwagę punkt A leżący na osi dipola w odległości r od jego środka 0. Natężenie
G
E A pola w punkcie A jest wypadkową natężeń pól wytwarzanych w punkcie A przez
G
G
ładunek +Q i –Q. Oba natężenia E + i E − są skierowane wzdłuż tej samej prostej, lecz mają
zwroty przeciwne, a zatem ich suma geometryczna sprowadza się do różnicy arytmetycznej:
G
G
G
EA = E+ + E−
EA =
1
Q
1
Q
⋅
−
⋅
,
4πε (r − a / 2 )2 4πε (r + a / 2 )2
EA =
Q (r + a / 2 )2 − (r − a / 2 )2
⋅
,
4πε (r + a / 2 )2 (r − a / 2 )2
26
EA =
Q r 2 + ra + a 2 / 4 − r 2 + ra − a 2 / 4
,
⋅
2
4πε
r2 − a2 / 4
EA =
1
2Qra
⋅
2
4πε 2
r − a2 / 4
(
(
)
)
Takie jest wyrażenie ogólne na natężenie pola w punktach leżących na osi dipola. Dla
punktów leżących daleko od ładunków dipola (tzn. gdy r>>a) otrzymujemy wzór przybliżony
E≈
1 2Qa
.
4πε r 3
Iloczyn ładunku Q dipola i odległości a nazywamy momentem dipola. Tę nową wielkość
traktujemy jako wektor o kierunku od ładunku ujemnego do ładunku dodatniego dipola i
G
oznaczamy symbolem p .
A zatem natężenie pola elektrycznego w punktach leżących na osi dipola w odległości r
znacznie większej od a wynosi
E≅
1 2p
4πε r 3
Zad.7.5.
Na powłoce kulistej o promieniu R rozmieszczone są równomiernie ładunki
elektryczne z gęstością powierzchniową σ. Znaleźć natężenie pola i potencjał w odległości r
od środka kuli.
Rozwiązanie:
Gęstość powierzchniowa σ ładunku mówi nam jaki ładunek elektryczny jest umieszczony na
jednostce powierzchni ciała.
σ=
dq C
ds m 2
Na powłoce kulistej o promieniu R umieszczony jest ładunek Q
Q = σ⋅S
gdzie S = 4πR 2 - pole powierzchni kuli.
Ładunek ten umieszczony jest tylko na powierzchni kuli tak, że wewnątrz kuli jak i na
zewnątrz nie ma innych ładunków.
27
Jeżeli współśrodkowo z powłoką kulistą o promieniu R utworzymy (w myślach)
powierzchnię kulistą o promieniu r, to na tej powierzchni (zwanej powierzchnią gaussowską)
G
G G
wektor E ma stałą wartość i jest zawsze prostopadły do powierzchni ( E d s ) i wtedy
G G
E ⋅ ds = Eds .
Stosujemy prawo Gaussa, które mówi, że strumień natężenia pola elektrycznego Φ E,S przez
powierzchnię zamkniętą S ( przez naszą utworzoną w myślach sferę o promieniu r) jest równy
całkowitemu ładunkowi Q zawartemu wewnątrz tej powierzchni (w naszym przypadku
ładunkowi Q znajdującego się na powierzchni kuli o promieniu R leżącej wewnątrz kuli o
promieniu r) pomnożonemu przez czynnik
1
.
ε
G G 1
Φ E,S = ∫ E ⋅ ds = ⋅ Q
ε
S
Ale
G G
Φ E,S = ∫ E ⋅ ds = ∫ E ⋅ ds = E ∫ ds = E ⋅ 4πr 2
S
S
S
Dla r<R (wewnątrz powłoki kulistej o promieniu R) ładunek Q nie występuje, więc
E ⋅ 4πr 2 = 0
i wtedy natężenie pola elektrycznego wewnątrz naładowanej powierzchniowo kuli wynosi
zero.
E=0
Dla r ≥ R czyli w przypadku gdy gaussowska powierzchnia ( ta utworzona przez nas w
myślach powierzchnia kulista o promieniu r) obejmuje naładowaną powłokę o promieniu R
prawo Gaussa możemy zapisać:
1
E ⋅ 4πr 2 = ⋅ Q
ε
E ⋅ 4πr 2 =
E(r ) =
σR 2
εr 2
;
1
⋅ 4πR 2 ⋅ σ
ε
dla r = R otrzymujemy :
E(R ) =
σ
ε
Zatem natężenie pola elektrycznego wewnątrz naładowanej powłoki kulistej jest równe zeru,
na jej powierzchni osiąga wartość σ/ε, następnie maleje odwrotnie proporcjonalnie do
kwadratu odległości i jest skierowane prostopadle do powierzchni kuli (rys.a).
28
Potencjał pola V wyznaczamy korzystając z wzoru definicyjnego, że
VA =
WA∞
q0
Dla r>R
∞G G ∞
G G ∞ σ R2
WA∞ = ∫ F ⋅ d r = ∫ q 0 ⋅ F ⋅ d r = ∫ q 0
dr
2
ε
r
r
r
r
q R 2σ ∞ 1
q 0R 2σ 1
=
WA∞ = 0
dr
−
∫ 2
ε
ε
r
r
r
q R 2σ 1
⋅
WA∞ = 0
ε
r
V(r ) =
∞
r
i wtedy
R 2σ
; dla r = R otrzymujemy :
εr
V(R ) =
σ⋅R
ε
Dla r ≤ R
∞ G G R
∞
σ R2
WA∞ = ∫ q 0 E ⋅ d r = ∫ q 0 0 ⋅ dr + ∫ q 0
dr
ε r2
r
r
R
∞
σR 2 1
WA∞ = 0 + q 0
−
ε r R
q Rσ
WA∞ = 0
ε
i wtedy
V(r ) =
R ⋅σ
= const
εr
Wykres funkcji V(r) przedstawia rys. b.
Zad. 7.6.
G
Znaleźć natężenie pola elektrycznego E w odległości r od nieskończenie długiej
prostoliniowej nici naładowanej ładunkiem elektrycznym z gęstością liniową λ.
29
Rozwiązanie:
Gęstość liniowa ładunku λ mówi nam jaki ładunek elektryczny jest umieszczony na jednostce
długości nici.
λ=
dQ C
dl m
Na odcinku nici o długości l umieszczony jest ładunek Q
Q =λ⋅l
Z symetrii układu (rozkładu ładunku)
G
wynika, że natężenie poła E będzie
skierowane prostopadle do powierzchni
bocznej nici.
Opierając się na twierdzeniu Gaussa
możemy zapisać:
G G
Q
Φ E,S = ∫ E ⋅ ds =
ε
S
gdzie
S
jest
powierzchnią
walca
współśrodkowego z nicią o wysokości l i
promieniu r.
G G
G G
G G
Φ E,S = ∫ E ⋅ ds = ∫ E ⋅ ds b + 2 ∫ E ⋅ ds pod
S
Sb
Spod
Ostatni człon w tym wyrażeniu znika, gdyż
strumień przechodzący przez podstawę
walca jest równy zeru, ponieważ
G
G G
G
ds pod ⊥ E , co czyni, że: E ⋅ ds pod = 0 .
Ze względu na stałą wartość
G
E
powierzchni bocznej walca zachodzi:
G
G G
G G
∫ E ⋅ ds = ∫ E ⋅ ds b = E ∫ ds = E 2πr ⋅ l
S
Zatem
1
E ⋅ 2πr ⋅ l = ⋅ Q
ε
30
Sb
Sb
na
1
E ⋅ 2πr ⋅ l = ⋅ λ ⋅ l
ε
E=
λ
2πε r
Zad.7.7.
Obliczyć pojemność C kondensatora cylindrycznego o promieniach elektrod
(cylindrów) R1 i R2 oraz długości l, wypełnionego dielektrykiem o przenikalności
elektrycznej ε.
Rozwiązanie:
Wychodzimy
ze
wzoru
definicyjnego
pojemności
C=
Q
Q Q
=
=
V1 − V2 ∆V U
Gdzie U to napięcie, (czyli różnica
potencjałów
∆V = V1 − V2
między
elektrodami kondensatora.
Na wewnętrznej elektrodzie cylindrycznej
o promieniu R1 znajduje się ładunek Q
równomiernie rozłożony na tej elektrodzie.
G
Z symetrii rozkładu ładunku wynika, że natężenie pola E w przestrzeni między elektronowej
będzie skierowane prostopadle do powierzchni pobocznicy walca (elektrody).
Jako powierzchnię Gaussa wybieramy powierzchnię walca o promieniu r i wysokości l,
którego oś symetrii pokrywa się z osią kondensatora (z osiami walców o R1 i R2).
Opierając się na twierdzeniu Gaussa możemy zapisać
G G
Q
Φ E,S = ∫ E ⋅ ds =
ε
S
gdzie S = S b + 2S pod jest powierzchnią całkowitą walca o promieniu r i wysokości l. Na
wielkość tej powierzchni S składa się powierzchnia pobocznicy walca
oraz dwie powierzchnie podstawy
S pod = πr 2
31
Zatem
S b = 2πr ⋅ l
G G
G G
G G
Φ E,S = ∫ E ⋅ ds = ∫ E ⋅ ds b + 2 ∫ E ⋅ ds pod
S
Sb
Spod
Ostatni człon w tym wyrażeniu zanika, gdyż strumień przechodzący przez podstawy walca
G
G G
G
jest równy zeru ponieważ dla l>>r ds pod ⊥ E co czyni, że: E ⋅ ds pod = 0 .
G
Ze względu na stałą wartość E na powierzchni bocznej walca gaussowskiego zachodzi:
G G
G G
∫ E ⋅ ds = ∫ E ⋅ ds = E ∫ ds = E 2πr ⋅ l
S
Sb
Sb
1
E ⋅ 2πr ⋅ l = ⋅ Q ;
ε
czyli
E=
Q 1
⋅
2πε l r
Znając E w przestrzeni międzyelektronowej obliczamy U
R2
U = ∆V = ∫ E(r ) ⋅ dr =
R1
U=
R
2
Q
Q R2 1
(ln r )
∫ dr =
2πεl
2πεl R r
R1
1
R
Q
Q
⋅ (ln R 2 − ln R 1 ) =
ln 2
2πεl
2πεl R 1
Ostatecznie pojemność C kondensatora wynosi
C=
Q
Q
=
U
R
Q
ln 2
2πεl R 1
2πεl
R
ln 2
R1
C=
=
2πεl
R
ln 2
R1
Zad.7.8.
N kondensatorów o pojemnościach C1 , C 2 , C 3 ,... , C j ,... , C N połączono w baterię
raz szeregowo, raz równoległe. Oblicz pojemność elektryczną powyższych baterii
kondensatorów.
Rozwiązanie:
a) połączenie szeregowe
32
Napięcie U przyłożone do baterii N szeregowo połączonych kondensatorów jest równe sumie
spadków napięć na poszczególnych kondensatorach
U = U1 + U 2 + U 3 + ... + U j + ... + U N
(*)
Na okładce każdego kondensatora zgromadzony jest jednakowy ładunek Q.
Z definicji pojemności C wynika, że
C=
Q
;
U
U1 =
Q
Q
Q
;...
; U3 =
; U2 =
C3
C2
C1
Uj =
Q
;...
Cj
UN =
Q
CN
Po podstawieniu do (*) otrzymujemy:
1
1
1
1
+
+
+ ... +
+ ...
U = Q
C1 C 2 C 3
Cj
1
C WS
=
1
CN
1
U 1
1
1
=
+
+
+ ... +
+ ...
Cj
Q C1 C 2 C 3
+
1
CN
Ostatecznie bateria kondensatorów utworzona z N kondensatorów połączonych szeregowego
ma pojemność CWS taką, że
1
C WS
=
1
1
1
1
+
+
+ ... +
+ ...
Cj
C1 C 2 C 3
+
1
CN
a) połączenie równoległe
Przy połączeniu równoległym kondensatorów na każdym
kondensatorze panuje to samo napięcie U, ale zgromadzony
jest na ich elektrodach inny ładunek.
Zatem ładunek całkowity Q zgromadzony w baterii
kondensatorów o pojemności CWR wynosi
Q = Q1 + Q 2 + Q 3 + ... + Q j + ... + Q N
(**)
Z definicji pojemności C wynika, że:
Q
;
U
Q1 = C1 U, Q 2 = C 2 U, ... , Q j = C j U,... , Q N = C N U
C=
oraz
Q = C WR ⋅ U
Po podstawieniu do (**) otrzymujemy
C WR ⋅ U = C1 U + C 2 U + C 3 U + ... + C j U + ... + C N ⋅ U
Ostatecznie C WR = C1 + C 2 + C 3 + ... + C j + ... + C N
33












