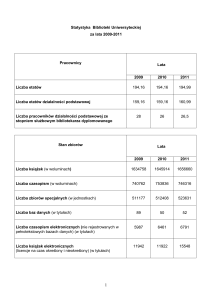
I kolokwium ze Wstępu do Teorii Miary
17.11.05
Grupa A
1. (a) Udowodnić, że lim(An ∩ Bn ) ⊂ lim An ∩ lim Bn .
(b) Znaleźć granice górną i dolną ciągu zbiorów:
An = (−1)n ·
1
1
, 1 − (−1)n ·
∪ [3, 4 + (−1)n ).
n
n
Rozwiązanie
a) x ∈ lim(An ∩ Bn ) wtedy i tylko wtedy, gdy x należy do nieskończenie
wielu przekrojów A ∩ B. Ale wtedy x ∈ An dla nieskończenie wielu n i
x ∈ Bn dla nieskończenie wielu n. Zatem należy jednocześnie do lim An
i lim Bn .
b) Dla każdego x z przedzialu (0, 1) istnieje takie n, że dla n > n0
zachodzi n1 < x < 1 − n1 . Zatem (0, 1) ⊂ lim An . Punkty z odcinka [3, 5]
nie należą do An dla nieparzystych, a spoza (0, 1) ∪ [3, 5] nie należą do
An dla parzystych n (zwykle dla żadnych), więc (0, 1) = lim An .
Dodatkowo, punkty 0, 1 należą do An dla nieparzystych n, a przedział
[3, 5] zawiera się w An dla parzystych n. Punkty z (−∞, 0) ∪ (1, 3) ∪
(5, ∞) należą do co najwyżej skończenie wielu An , więc lim An = [0, 1]∪
[3, 5].
2. Znaleźć σ-ciało generowane w Z przez rodzinę wszystkich trzyelementowych zbiorów postaci {2n, 2n + 1, 2n + 2} (n ∈ Z). Odpowiedź uzasadnić.
Rozwiązanie
Dowiedziemy, że jest to 2Z , czyli rodzina wszystkich
podzbiorów Z. Jest jasne, że jest to σ-ciało, bo skoro zawiera wszystkie
podzbiory Z, to jest zamknięte na wszystkie możliwe operacje mnogościowe. Oczywiście, zawiera też zbiory trzyelementowe danej postaci, bo
zawiera wszystkie podzbiory. Wystarczy więc uzasadnić, że każdy zbiór
da się uzyskać z trzyelementowych zbiorów postaci {2n, 2n + 1, 2n + 2}
przez działania nie wyprowadzające (ogólnie) poza σ-ciało. Ponieważ
każdy podzbiór Z jest przeliczalną sumą zbiorów jednoelementowych,
wystarczy wygenerować zbiory jednoelementowe.
Dla n parzystych, czyli postaci n = 2k, mamy
{n} = {2k, 2k + 1, 2k + 2} ∩ {2k − 2, 2k − 1, 2k},
zatem potrafimy wygenerować singletony parzyste. Wobec tego dla n
nieparzystych, n = 2k + 1, możemy zapisać
{n} = {2k, 2k + 1, 2k + 2} \ {2k} \ {2k + 1},
1
co kończy dowód.
3. Zdefiniujmy σ-ciało borelowskie B na R jako najmniejsze σ-ciało zawierające wszystkie przedziały otwarte. Udowodnić, że B jest generowane
przez rodzinę {(−∞, q] : q ∈ Q}.
Rozwiązanie
Oznaczmy przez A σ-ciało generowane przez daną
rodzinę. Zauważmy, że dla każdej liczby a ∈ R mamy
∞
[
(−∞, a) =
(−∞, qn ],
n=1
gdy (qn ) jest rosnącym ciągiem liczb wymiernych zbieżnym do a. Podobnie,
∞
\
(−∞, a] =
(−∞, qn ],
n=1
gdy (qn ) jest malejącym ciągiem liczb wymiernych zbieżnym do a. Zatem półproste (−∞, a), (−∞, a] należą do A dla wszystkich a ∈ R.
Ponieważ, dla dowolnych a < b ∈ R mamy
c
(a, b) = (−∞, b) ∩ (−∞, a] ,
każdy przedział otwarty musi należeć do A. Czyli B ⊂ A.
Z drugiej strony, (q, ∞) można zapisać, na przykład, jako przeliczalną
S
c
sumę przedziałow otwartych ∞
n=1 (q, q + n). Zatem (−∞, q] = (q, ∞)
należy do B, czyli A ⊂ B.
4. Niech (X, F) będzie przestrzenią mierzalną. Ustalmy skończony zbiór
{x1 , ..., xk } ⊂ X. Czy funkcja zbioru µ : F → [0, ∞] określona wzorem
µ(A) =
k
X
A (xi )
i=1
jest miarą?
Rozwiązanie
Miara jest nieujemną przeliczalnie addytywną funkcją zbioru spełniającą przypisująca zbiorowi pustemu 0. Skoro µ jest sumą wartości funkcji nieujemnych, to jest nieujemna. Ponadto ∅ (x) = 0
dla każdego x, więc µ(∅) = 0. Rozważmy teraz ciąg (An ) zbiorów paS
rami rozłącznych. Niech A = ∞
n=1 An . Dla każdego i = 1, ..., k mamy
A (xi ) = 1 wtedy i tylko wtedy, gdy istnieje taki n(k), że An(k) (xi ) = 1.
Zatem
k
X
A (xi ) =
k
X
i=1
i=1
2
An(k) (xi )
Co więcej, taki n może być tylko jeden dzięki rozłączności, więc
k
X
An(k) (xi ) =
k X
∞
X
An (xi ).
i=1 n=1
i=1
Zamieniając kolejność sumowania na mocy twierdzeń o arytmetyce graP
nic, mamy µ(A) = ∞
n=1 An .
5. Które z poniższych zdań są fałszywe, a które prawdziwe? Odpowiedzi
nie trzeba uzasadniać. Za dobrą odpowiedź dodajemy 1 punkt, za złą
odejmujemy 1 punkt. Brak odpowiedzi nie jest punktowany.
(a) Jeśli An jest wstępującym lub zstępującym ciągiem zbiorów mierzalnych (w pewnej przestrzeni mierzalnej), to lim An jest zbiorem
mierzalnym.
(b) Każde σ-ciało jest rodziną monotoniczną.
(c) µ(A \ B) = µ(A) − µ(B).
(d) Jeśli µ jest miarą i
T∞
n=1
S∞
An = ∅, to µ (
(e) Zbiory typu Fσ są borelowskie.
n=1
An ) =
P∞
n=1
µ(An ).
Rozwiązanie
T (wtedy granice są odpowienio przeliczalną sumą lub przeliczalnym przekrojem);
T (skoro jest zamknięte na wszystkie przeliczalne sumy i przekroje, to tym
bardziej na monotoniczne);
N (nie jest tak np. gdy A ∩ B = ∅ i µ(B) > 0);
N (za słabe założenie);
T (Fσ to przeliczalne sumy zbiorów domkniętych, więc borelowskich).
3
I kolokwium ze Wstępu do Teorii Miary
17.11.05
Grupa B
1. (a) Udowodnić, że lim An ∪ lim Bn ⊂ lim(An ∪ Bn ).
(b) Znaleźć granice górną i dolną ciągu zbiorów:
(−1)n
(−1)n
+
2,
3
−
.
Bn = (−2n, −n) ∪
2n
3n
"
!
Rozwiązanie
a) Jeśli x należy do An dla prawie wszystkich n, to tym bardziej należy
do An ∪ Bn dla prawie wszystkich Bn . Zatem lim An ⊂ lim(An ∪ Bn ).
Podobnie dla Bn .
b) Dla każdego x z przedzialu (2, 3) istnieje takie n0 , że dla n > n0
zachodzi 2 + 21n ¬ x < 3 − 31n . Zatem (2, 3) ⊂ lim An . Każda liczba
ujemna należy do (−2n, −n) dla co najwyżej skończenie wielu n, a każda dodatnia, za wyjątkiem przedziału (2, 3) do co najwyżej skończenie
wielu [2 − 21n , 3 + 31n ). Zatem (2, 3) = lim An
Dodatkowo, punkty 2, 3 należą do An dla nieparzystych n. Punkty
z (−∞, 2) ∪ (3, ∞) należą do co najwyżej skończenie wielu An , więc
lim An = [2, 3].
2. Znaleźć σ-ciało generowane w Z przez rodzinę wszystkich trzyelementowych zbiorów postaci {n, 2n, 3n} (n ∈ Z). Odpowiedź uzasadnić.
Rozwiązanie
Dowiedziemy, że jest to 2Z , czyli rodzina wszystkich
podzbiorów Z. Jest jasne, że jest to σ-ciało, bo skoro zawiera wszystkie
podzbiory Z, to jest zamknięte na wszystkie możliwe operacje mnogościowe. Oczywiście, zawiera też zbiory trzyelementowe danej postaci,
bo zawiera wszystkie podzbiory. Wystarczy więc uzasadnić, że każdy
zbiór da się uzyskać z trzyelementowych zbiorów postaci {n, 2n, 3n}
przez działania nie wyprowadzające (ogólnie) poza σ-ciało. Ponieważ
każdy podzbiór Z jest przeliczalną sumą zbiorów jednoelementowych,
wystarczy wygenerować zbiory jednoelementowe. Ale
{n} = {n, 2n, 3n} \ {2n, 4n, 6n} \ {3n, 6n, 9n}.
3. Zdefiniujmy σ-ciało borelowskie B na R jako najmniejsze σ-ciało zawierające wszystkie przedziały otwarte. Udowodnić, że B jest generowane
przez rodzinę {[q, ∞) : q ∈ Q}.
4
Rozwiązanie
Oznaczmy przez A σ-ciało generowane przez daną
rodzinę. Zauważmy, że dla każdej liczby a ∈ R mamy
(a, ∞) =
∞
[
[qn , ∞),
n=1
gdy (qn ) jest malejącym ciągiem liczb wymiernych zbieżnym do a. Podobnie,
[a, ∞) =
∞
\
[qn , ∞),
n=1
gdy (qn ) jest rosnącym ciągiem liczb wymiernych zbieżnym do a. Zatem
półproste (a, ∞), [a, ∞) należą do A dla wszystkich a ∈ R. Ponieważ,
dla dowolnych a < b ∈ R mamy
c
(a, b) = (a, ∞) ∩ [b, ∞) ,
każdy przedział otwarty musi należeć do A. Czyli B ⊂ A.
Z drugiej strony, (−∞, q) można zapisać, na przykład, jako przeliczalną
S
c
sumę przedziałow otwartych ∞
n=1 (q − n, q). Zatem [q, ∞) = (−∞, q)
należy do B, czyli A ⊂ B.
4. Niech (X, F) będzie przestrzenią mierzalną. Czy funkcja zbioru µ : F →
[0, ∞] określona wzorem
liczność A,
µ(A) =
∞,
gdy A jest skończony
w przeciwnym wypadku
jest miarą? (Przyjmujemy zgodnie z intuicją: ∞+∞ = ∞, ∞+a = ∞,
∞ > a dla każdej a ∈ R.)
Rozwiązanie
Miara jest nieujemną przeliczalnie addytywną funkcją zbioru spełniającą przypisująca zbiorowi pustemu 0. Skoro µ jest
licznością zbioru, to jest nieujemna (ewentualnie +∞). Ponadto liczność zbioru pustego wynosi 0, więc µ(∅) = 0. Rozważmy teraz ciąg
S
(An ) zbiorów parami rozłącznych. Niech A = ∞
An . Jeśli któryś z
n=1 P
An jest nieskończony, to A też, więc mamy µ(A) = ∞
n=1 µ(An ) = ∞.
Załóżmy więc, że An są skończone. Jeśli A jest nieskończony, to musi nieskończenie wiele spośrod An musi być niepustych. Zatem szereg
P∞
) ma nieskończenie wiele składników nie mniejszych niż jen=1 µ(AnP
den, więc ∞
n=1 µ(An ) = ∞ = µ(A). Jeśli zaś A jest skończony, to
prawie wszystkie An muszą być puste. Ponieważ suma liczności dwóch
(zatem i skończonej liczby) skończonych zbiorów rozłącznych jest równa
liczności ich sumy, mamy tezę.
5
5. Które z poniższych zdań są fałszywe, a które prawdziwe? Odpowiedzi
nie trzeba uzasadniać. Za dobrą odpowiedź dodajemy 1 punkt, za złą
odejmujemy 1 punkt. Brak odpowiedzi nie jest punktowany.
(a) Jeśli (An ) jest ciągiem zbiorów mierzalnych (w pewnej przestrzeni
mierzalnej), to lim inf n An i lim supn An są zbiorami mierzalnymi.
(b) Niech {At : t ∈ T } będzie dowolną (niekoniecznie przeliczalną)
S
rodziną zbiorów miary zero. Wtedy µ ( t∈T At ) = 0.
(c) Przekrój rodziny σ-ciał jest zawsze σ-ciałem.
(d) Jeśli µ jest miarą i µ(A∪B) = µ(A)+µ(B), to A i B są rozłączne.
(e) Zbiory typu Gδ są borelowskie.
Rozwiązanie
T (granice górna polegają na zastosowaniu przeliczalnego przekroju i
przeliczalnej sumy);
N (cała przestrzeń może być sumą zbiorów miary zero, np. dla R zbiorów jednopunktowych);
T (to po prostu trzeba wiedzieć);
N (przekrój może być niepusty, ale miary zero);
T (Gδ to przeliczalne przekroje zbiorów otwartych, więc borelowskich).
6