funkcje

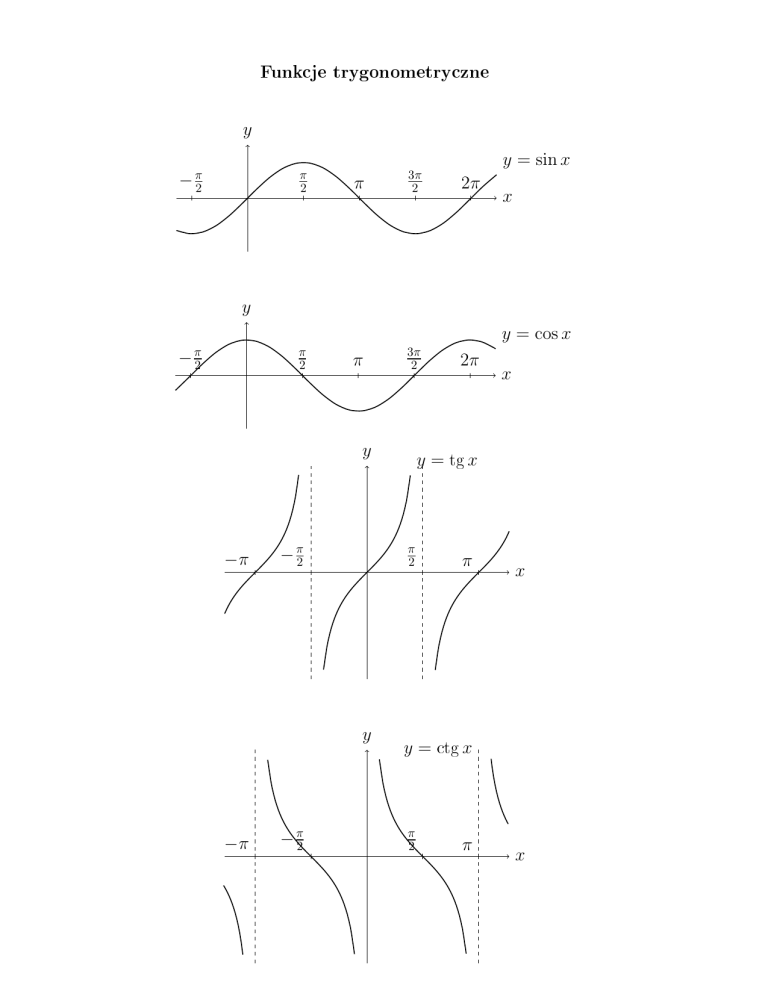
Funkcje trygonometryczne
y
y = sin x
− π2
π
2
π
3π
2
2π
x
y
y = cos x
− π2
π
2
π
3π
2
y
−π
− π2
−π
− π2
x
y = tg x
π
2
y
2π
π
x
y = ctg x
π
2
π
x
Funkcje cyklometryczne
Funkcjami cyklometrycznymi nazywamy funkcje odwrotne do funkcji trygonome-
trycznych zaw¦»onych do odpowiednich zbiorów. Mo»na je zdeniowa¢ jednoznacznie
tylko w tych przedziaªach, w których funkcje trygonometryczne s¡ ró»nowarto±ciowe.
Wykresy funkcji cyklometrycznych sporz¡dza si¦ zgodnie z zasad¡ sporz¡dzania
wykresów funkcji odwrotnych, tzn. przez odbicie symetryczne wzgl¦dem prostej y = x
wykresów funkcji trygonometrycznych w odpowiednich przedziaªach.
Niech f : − π2 , π2 → [−1, 1], f (x) = sin x. Funkcja f jest bijekcj¡, zatem mo»na
utworzy¢ funkcj¦
π π do
niej odwrotn¡. Funkcj¦ odwrotn¡ do funkcji sinus zaw¦»onej do
przedziaªu − 2 , 2 nazywamy arcus sinus i oznaczamy symbolem arcsin. Mamy
h π πi
.
arcsin x = y ⇐⇒ sin y = x dla x ∈ [−1, 1] , y ∈ − ,
2 2
Dziedzin¡ funkcji arcus sinus jest zbiór D = [−1, 1].
y
y = arcsin x
π
2
−1
− π2
1
x
Niech f : [0, π] → [−1, 1], f (x) = cos x. Funkcj¦ odwrotn¡ do funkcji cosinus zaw¦»onej do przedziaªu [0, π] nazywamy arcus cosinus i oznaczamy symbolem arccos.
Mamy
arccos x = y ⇐⇒ cos y = x dla x ∈ [−1, 1] , y ∈ [0, π] .
Dziedzin¡ funkcji arcus cosinus jest zbiór D = [−1, 1].
y
π
π
2
−1
y = arccos x
1
x
Niech f : − π2 , π2 →R, f (x) = tg x. Funkcj¦ odwrotn¡ do funkcji tangens zaw¦»onej
do przedziaªu − π2 , π2 nazywamy arcus tangens i oznaczamy symbolem arctg . Mamy
π π
arctg x = y ⇐⇒ tg y = x dla x ∈ R, y ∈ − ,
.
2 2
Dziedzin¡ funkcji arcus tangens jest zbiór R.
yπ
2
y = arctg x
x
− π2
Mamy
arctg 0 = 0
√
π
3
√
3 π
=
arctg
3
6
π
arctg 1 =
4
π
arctg (−1) = − .
4
arctg
3=
Niech f : (0, π) → R, f (x) = ctg x. Funkcj¦ odwrotn¡ do funkcji cotangens zaw¦»onej do przedziaªu (0, π) nazywamy arcus cotangens i oznaczamy symbolem
arcctg . Mamy
arcctg x = y ⇐⇒ ctg y = x
dla
x ∈ R, y ∈ (0, π) .
Dziedzin¡ funkcji arcus cotangens jest zbiór R.
y
π
π
2
y = arcctg x
x
Mamy
π
2
√
π
arcctg 3 =
6
√
3 π
arcctg
=
3
3
π
arcctg 1 =
4
3
arcctg (−1) = π.
4
Podstawowe to»samo±ci zwi¡zane z funkcjami cyklometrycznymi:
arcctg 0 =
arcsin(−x) = − arcsin x
arctg (−x) = −arctg x
π
arcsin x + arccos x =
2
π
arctg x + arcctg x =
2
dla ka»dego
dla ka»dego
x ∈ [−1, 1],
x ∈ R,
dla ka»dego
x ∈ [−1, 1],
dla ka»dego
x ∈ R.
Funkcje wymierne
Funkcj¡ wymiern¡ nazywamy funkcj¦ postaci f (x) =
wielomianami odpowiednio stopnia m i n.
Wm (x)
Gn (x) ,
gdzie Wm (x) i Gn (x) s¡
Je»eli m < n, to funkcj¦ wymiern¡ f (x) nazywamy funkcj¡ wymiern¡ wªa±ciw¡, w
przeciwnym przypadku nazywamy j¡ funkcj¡ wymiern¡ niewªa±ciw¡.
Funkcj¦ wymiern¡ postaci f (x) =
wamy funkcj¡ homograczn¡.
ax+b
cx+d ,
gdzie c 6= 0, ad − bc 6= 0, a, b, d ∈ R, nazy-
Funkcje wymierne postaci f (x) =
prostymi pierwszego rodzaju.
1
(x+a)n ,
gdzie n ∈ N, a ∈ R, nazywamy uªamkami
2
2
2
Funkcje wymierne postaci f (x) = (x2Ax+B
+bx+c)n , gdzie n ∈ N, b −4c < 0 oraz A +B > 0,
nazywamy uªamkami prostymi drugiego rodzaju.
Nierówno±ci wymierne
Wm (x)
> 0 ⇐⇒ Wm (x)Gn (x) > 0
Gn (x)
Wm (x)
< 0 ⇐⇒ Wm (x)Gn (x) < 0
Gn (x)
Wm (x)
> 0 ⇐⇒ Wm (x)Gn (x) > 0 ∨ Wm (x) = 0
Gn (x)
Wm (x)
6 0 ⇐⇒ Wm (x)Gn (x) < 0 ∨ Wm (x) = 0
Gn (x)
Ci¡gi
Niech X b¦dzie zadanym zbiorem niepustym. Ci¡giem w zbiorze X nazywamy
ka»d¡ funkcj¦ a : N → X. Ci¡g w zbiorze liczb rzeczywistych R nazywamy ci¡giem
liczbowym. Ci¡g liczbowy oznacza¢ b¦dziemy symbolem {an }.
Ci¡g {an } jest ograniczony z doªu, je»eli istnieje liczba m ∈ R taka, »e dla ka»dej liczby
naturalnej n zachodzi an > m.
Ci¡g {an } jest ograniczony z góry, je»eli istnieje liczba M ∈ R taka, »e dla ka»dej
liczby naturalnej n zachodzi an 6 M.
Ci¡g, który jest jednocze±nie ograniczony z góry i z doªu nazywamy ci¡giem ograniczonym.
n
Ci¡g an = 2 + ( 53 ) jest ograniczony z doªu, bo np. an > 2 dla
n = 1, 2, . . ., ale nie jest ograniczony z góry.
Ci¡g bn = sin n jest ograniczony z góry i z doªu, bo bn 6 1 oraz bn > −1.
Przykªad 1.
Ci¡g {an } nazywamy
1) rosn¡cym, je»eli an < an+1 dla ka»dego n ∈ N,
2) niemalej¡cym, je»eli an 6 an+1 dla ka»dego n ∈ N,
3) malej¡cym, je»eli an > an+1 dla ka»dego n ∈ N,
4) nierosn¡cym, je»eli an > an+1 dla ka»dego n ∈ N.
Ci¡gi malej¡ce, rosn¡ce, niemalej¡ce i nierosn¡ce nazywamy ci¡gami monotonicznymi,
przy czym ci¡gi rosn¡ce i malej¡ce nazywamy ±ci±le monotonicznymi, a ci¡gi nierosn¡ce
i niemalej¡ce sªabo monotonicznymi.
Przy badaniu monotoniczno±ci ci¡gów wygodnie jest bada¢ znak ró»nicy an+1 − an .
Przykªad 2.
Zbadamy, czy ci¡g an =
n
n2 +1
jest monotoniczny.
Dla ka»dego n ∈ N mamy
an+1 =
n+1
n+1
=
.
(n + 1)2 + 1 n2 + 2n + 2
Tworzymy ró»nic¦ an+1 − an i otrzymujemy
n+1
n
−
=
n2 + 2n + 2 n2 + 1
(n + 1)(n2 + 1) − n(n2 + 2n + 2)
=
=
(n2 + 2n + 2)(n2 + 1)
n3 + n + n2 + 1 − n3 − 2n2 − 2n
=
=
(n2 + 2n + 2)(n2 + 1)
−n2 − n + 1
=
.
(n2 + 2n + 2)(n2 + 1)
an+1 − an =
Poniewa» dla ka»dej liczby naturalnej n prawdziwa jest nierówno±¢
−n2 − n + 1
< 0,
(n2 + 2n + 2)(n2 + 1)
wi¦c badany ci¡g {an } jest malej¡cy.
Granica ci¡gu
Liczb¦ a nazywamy granic¡ wªa±ciw¡ ci¡gu {an } (piszemy lim an = a lub an → a),
n→∞
je»eli jest speªniony warunek
∀ε>0 ∃n0 ∈N ∀ n∈N |an − a| < ε.
n>n0
Poniewa» mamy
|an − a| < ε ⇐⇒ −ε < an − a < ε ⇐⇒ a − ε < an < a + ε,
wi¦c mo»emy powiedzie¢, »e liczba a jest granic¡ ci¡gu {an }, je»eli w ka»dym przedziale
(a − ε, a + ε) znajduj¡ si¦ prawie wszystkie wyrazy tego ci¡gu.
Okre±lenie prawie wszystkie wyrazy ci¡gu oznacza, »e poza przedziaªem (a − ε, a + ε)
znajduje si¦ sko«czona liczba wyrazów tego ci¡gu.
Je»eli granic¡ ci¡gu {an } jest liczba a, to mówimy, »e ci¡g {an } jest zbie»ny do a.
Mówimy, »e ci¡g {an } ma granic¦ niewªa±ciw¡ równ¡ +∞ (piszemy lim an = +∞),
n→∞
je»eli jest speªniony warunek
∀ε>0 ∃n0 ∈N ∀ n∈N an > ε.
n>n0
Mówimy, »e ci¡g {an } ma granic¦ niewªa±ciw¡ równ¡ −∞ (piszemy lim an = −∞),
n→∞
je»eli jest speªniony warunek
∀ε<0 ∃n0 ∈N ∀ n∈N an < ε.
n>n0
W obu powy»szych przypadkach mówimy, »e ci¡g {an } jest zbie»ny do granicy niewªa±ciwej.
Twierdzenie 1
Ka»dy ci¡g ma co najwy»ej jedn¡ granic¦.
Twierdzenie 2
Ka»dy ci¡g zbie»ny do granicy wªa±ciwej jest ograniczony.
Twierdzenie 3
Je»eli lim |an | = +∞, to lim
Np. lim
1
n→∞ −n
1
n→∞ n
n→∞
= 0, lim
Twierdzenie 4
1
n→∞ an
= 0.
= 0.
Je»eli ci¡gi {an } i {bn } maj¡ granice wªa±ciwe, to
a) lim (an + bn ) = lim an + lim bn ,
n→∞
b)
c)
n→∞
n→∞
lim (an − bn ) = lim an − lim bn ,
n→∞
n→∞
n→∞
lim (an · bn ) = lim an · lim bn ,
n→∞
n→∞
n→∞
d) lim (kan ) = k lim an dla k ∈ R,
n→∞
n→∞
lim an
an
n→∞
=
o ile lim bn 6= 0,
e) lim
n→∞
n→∞ bn
lim bn
n→∞
m
m
f ) lim (an ) = lim an
dla m ∈ Z,
n→∞
n→∞
q
√
p
g) lim an = p lim an dla p ∈ N, p > 2.
n→∞
n→∞