Przypominajka : Algorytmy grafowe w służbie sekwencjonowania DNA
oraz identyfikacji protein
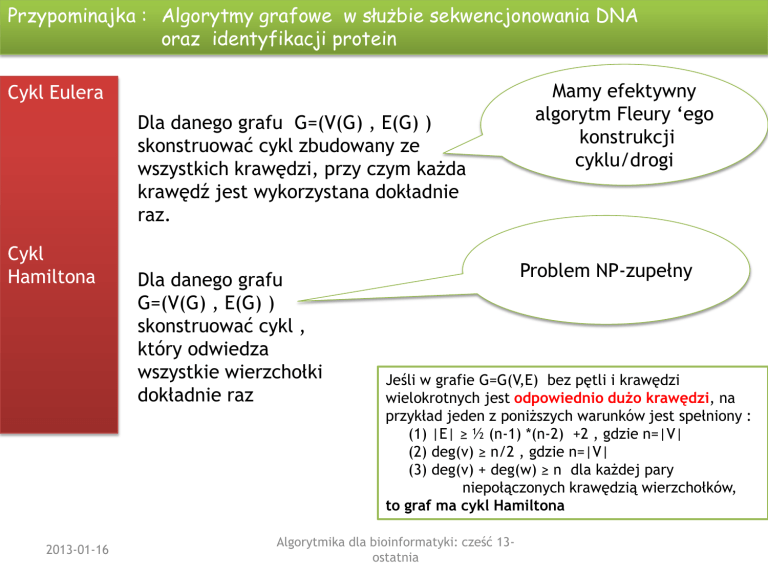
Cykl Eulera
Dla danego grafu G=(V(G) , E(G) )
skonstruować cykl zbudowany ze
wszystkich krawędzi, przy czym każda
krawędź jest wykorzystana dokładnie
raz.
Cykl
Hamiltona
2013-01-16
Dla danego grafu
G=(V(G) , E(G) )
skonstruować cykl ,
który odwiedza
wszystkie wierzchołki
dokładnie raz
Mamy efektywny
algorytm Fleury ‘ego
konstrukcji
cyklu/drogi
Problem NP-zupełny
Jeśli w grafie G=G(V,E) bez pętli i krawędzi
wielokrotnych jest odpowiednio dużo krawędzi, na
przykład jeden z poniższych warunków jest spełniony :
(1) |E| ≥ ½ (n-1) *(n-2) +2 , gdzie n=|V|
(2) deg(v) ≥ n/2 , gdzie n=|V|
(3) deg(v) + deg(w) ≥ n dla każdej pary
niepołączonych krawędzią wierzchołków,
to graf ma cykl Hamiltona
Algorytmika dla bioinformatyki: cześć 13ostatnia
Grafy i genetyka
Genialna obserwacja Seymoura Benzera (1950)
dowodząca , że struktura genu jest liniowa
Watson i Crick
odkryli strukturę
podwójnej helisy
DNA w 1953
Normalny wirus T4 zabija pewną bakterię
Ale, jeśli T4 jest zmutowane (ważny część genu jest skasowana),
to wirus traci moc zabijania bakterii.
Przypuśćmy, że bakteria jest zarażona dwoma takimi różnymi
mutantami .
Czy taki atak bakteria przeżyje czy nie?
Zadziwiające, ale para różnych zmutowanych wirusów może zabić
bakterie mimo, że każdy mutant z osobna nie zabija.
Jak to można wytłumaczyć?
2013-01-16
Algorytmika dla bioinformatyki: cześć 13ostatnia
W
M1
M2
M3
Mutacje M1 i M2
pokrywają się
2013-01-16
Algorytmika dla bioinformatyki: cześć 13ostatnia
Grafy i genetyka
Dwie
hipotetyczne
struktury
organizacyjne
genu:
a) organizacja
liniowa
b) organizacja z
rozgałęzieniami
Nie jest możliwa
konstrukcja liniowej
sekwencji delecji taka,
która prowadzi do tego
grafu
2013-01-16
Algorytmika dla bioinformatyki: cześć 13ostatnia
Graf interwałowy
Delecje i ich interwały
Przykład grafu
interwałowego
Niemożliwe jest
wskazanie delecji tak,
aby spełnione były
relacje grafu.
Przykład grafu
nie
interwałowego
2013-01-16
Algorytmika dla bioinformatyki: cześć 13ostatnia
Sekwencjonowanie DNA
Eksperyment Sangera:
2013-01-16
Masz wiele egzemplarzy tej samej gazety
pociętych na miliony części.
Każdy egzemplarz jest pocięty inaczej.
Znaczna część kawałków się pogubiła.
Znaczna część jest pochlapana atramentem.
Potrafisz odczytać oryginalną zawartość?
Algorytmika dla bioinformatyki: cześć 13ostatnia
Graf zupełny
skierowany
z wagami
wyznaczonymi
przez POKRYCIE
etykiet
wierzchołków
2013-01-16
Algorytmika dla bioinformatyki: cześć 13ostatnia
Sekwencjonowanie DNA przez Hybrydyzacje
• 1988: pierwsze pomysły dla
macierzy DNA. Mało kto
wierzy w powodzenie
• 1991: technika syntezy
polimerów sterowana
światłem (light directed
polymer synthesis)
• 1994: pierwsza 64-kb
micromacierz DNA
2013-01-16
First microarray
prototype (1989)
First commercial
DNA microarray
prototype w/16,000
features (1994)
500,000 features
per chip (2002)
Algorytmika dla bioinformatyki: cześć 13ostatnia
Sekwencjonowanie DNA przez Hybrydyzacje:
Na czym polega?
2013-01-16
Algorytmika dla bioinformatyki: cześć 13ostatnia
Sekwencjonowane
DNA przykleiło się
do:
SuperŁańcuch:
Sekwencjonowane
DNA to ciąg
komplementarny:
Przykład uniwersalnej macierzy dla l-merów o długości l=4
2013-01-16
Algorytmika dla bioinformatyki: cześć 13ostatnia
Def:
spectrum(s,l) - widmo sekwencji DNA s w reprezentacji l-merów to
zbiór ujawnionych l-merów w eksperymencie sekwencjonowania DNA
UWAGA:
Różne sekwencje DNA mogą produkować to samo widmo!!
Spectrum( GTATCT ,2) = Spectrum( GTCTAT ,2) = {AT, CT, GT, TA, TC}
2013-01-16
Algorytmika dla bioinformatyki: cześć 13ostatnia
Rozwiązanie problemu SBH jako ścieżki Hamiltona w
grafie pokrywania się l-merów
Graf skierowany H
o wierzchołkach etykietowanych l-merami
o krawędziach jedynie wtedy, gdy pokrywanie wynosi l-1
Przykład:
S = { ATG AGG TGC TCC GTC GGT GCA CAG }
ATG AGG
TGC
H
ATG C A G G T C C
2013-01-16
TCC
GGT
GTC
GCA
CAG
Ścieżka odwiedziła każdy
wierzchołek tylko RAZ
Algorytmika dla bioinformatyki: cześć 13ostatnia
Problem
niejednoznaczności
wyniku
2013-01-16
Algorytmika dla bioinformatyki: cześć 13ostatnia
Rozwiązanie problemu SBH
jako ścieżki Eulera
Graf skierowany
o wierzchołkach etykietowanych l-1 merami
o krawędziach jedynie wtedy, gdy odpowiedni l mer występuje
w zbiorze widma
Przykład:
S = { ATG, TGG, TGC, GTG, GGC, GCA, GCG, CGT }
Wierzchołki: V = { AT, TG, GC, GG, GT, CA, CG }
GT
AT
E=S
CG
TG
GC
GG
2013-01-16
Krawędzie:
CA
ścieżka przechodząca przez
każdą krawędź i to tylko raz
Algorytmika dla bioinformatyki: cześć 13ostatnia
2013-01-16
Algorytmika dla bioinformatyki: cześć 13ostatnia