Nadprzewodnictwo

Nadprzewodnictwo
Opis fenomenologiczny
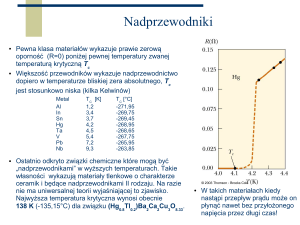
W 1911 roku Kammerlingh Onnes odkrył, że rtęć
poniżej pewnej temperatury zaczyna
nadprzewodzić,co oznacza, że jej opór elektryczny
wynosi 0.
Nagroda Nobla 1913
Właściwości nadprzewodników
• W stanie nadprzewodzącym substancja
posiada następujące cechy:
– Opór elektryczny równy jest zeru;
– Materiał staje się doskonałym
diamagnetykiem;
– Zmieniają się właściwości termiczne;
– Zmieniają się właściwości optyczne (w
zakresie pewnych częstotliwości);
• Normalny przewodnik przechodzi do stanu
nadprzewodzącego poniżej temperatury
krytycznej, Tc, Wartość temperatury krytycznej
zależy od natężenia zewnętrznego pola
magnetycznego ( Hc ) i jest maksymalna w
nieobecności pola.
Właściwości termiczne: energia swobodna
•
•
•
Wielkoscią decydującą o tym, jaki stan w danych warunkach
zewnętrznych jest stabilny jest potencjał termodynamiczny
Gibbsa na jednostkę objętosci:
G = U − TS + pV − BM
, gdzie M jest namagnesowaniem. W stanie nadprzewodzącym
materiał jest doskonałym diamagnetykiem, a zatem wypadkowe
pole magnetyczne wewnątrz materialu jest ròwne zeru:.
B wewn = B + µ 0 M = 0
•
Zatem, otrzymujemy układ równań:
dG = dU − TdS − SdT + pdV + Vdp − dBM − dMB
dU = TdS − pdV + BdM
M =−
•
1
µ0
B
Przyjmując, że p,V =const, otrzymujemy:
dG = −SdT +
1
BdB
µ0
Właściwości termiczne: energia swobodna
•
Oznaczając indeksem S stan nadprzewodzący, różnica energii
swobodnych Gibbsa pomiędzy stanem nadprzewodzącym w
polu magnetycznym B< BC(T) a stanem nadprzewodzącym
bez pola magnetycznego w stałej temperaturze T<TC będzie
równa:
B
G S ( B, T ) − G S (0, T ) =
∫
0
•
BdB B 2
=
µ0
2µ 0
Gdy pole magnetyczne osiąga wartość pola krytycznego,
wówczas materiał przechodzi do stanu normalnego
G S (B C , T) = G N (B C , T)
•
Energia swobodna stanu normalnego bardzo słabo zależy od
pola magnetycznego, zatem
G S (B C , T) = G N (B C , T) = G N (0, T)
•
otrzymujemy:
BC 2
G S (B C , T) − G S (0, T) = G N (0, T) − G S (0, T) =
2µ 0
BC 2 − B2
G N (B, T) − G S (B, T) =
2µ 0
Energia swobodna stanu nadprzewodzącego (poniżej Tc i Bc)
jest mniejsza niż stanu normalnego
Właściwości termiczne: entropia
dG = −SdT +
1
BdB
µ0
•
Ponieważ
•
Entropia i różnica entropii między stanami normalnym i
nadprzewodzącym, są odpowiednio równe:
⎛ ∂G ⎞
S = −⎜
⎟
⎝ ∂T ⎠ B = const
•
•
⎛ ∂ (∆G ) ⎞
∆ S = −⎜
⎟
∂
T
⎝
⎠ B = const
Stosując przybliżone wyrażenie na zależność pola krytycznego
od temperatury:
Otrzymujemy:
⎡ ⎛T
BC (T ) = BC (0) ⎢1 − ⎜⎜
⎢⎣ ⎝ TC
⎞
⎟⎟
⎠
2
⎤
⎥
⎥⎦
2
2
⎛ T ⎞ ⎟
2BC2 (0) ⎡⎢ ⎛ T ⎞ ⎤⎥
∂
1 − ⎜⎜ ⎟⎟
T 1 − ⎜⎜ ⎟⎟
= ..... =
∆S = SN − SS = −
2
⎜
⎟
T
∂T 2µ 0
⎢ ⎝ TC ⎠ ⎥
TC
⎣
⎦
⎝ ⎝ C⎠ ⎠
BC2 (0) ⎛⎜
2⎞
Entropia stanu nadprzewodzącego jest mniejsza niż stanu
normalnego
Właściwości termiczne: pojemność cieplna
•
•
∂S
C
=
T
Ponieważ V
∂T
⎡ ⎛T
BC (T ) = BC (0) ⎢1 − ⎜⎜
⎢⎣ ⎝ TC
2
⎤
⎥
⎥⎦
różnica pojemności cieplnej (ciepła właściwego) między
stanami normalnym i nadprzewodzącym, są odpowiednio
równe:
2 BC2 (0) d ⎛⎜ ⎡ ⎛ T
CN − CS = T
T ⎢1 − ⎜⎜
2
⎜
TC dT
T
⎝ ⎢⎣ ⎝ C
•
⎞
⎟⎟
⎠
⎞
⎟⎟
⎠
2
⎤⎞
⎥⎟
⎥⎦ ⎟⎠
Przekształcając dalej otrzymujemy:
⎛T
2 B (0) ⎡
⎜⎜
∆C = T
−
1
3
⎢
2
TC ⎢
⎝ TC
⎣
2
C
⎞
⎟⎟
⎠
2
⎤
⎥
⎥⎦
W temperaturze krytycznej następuje skokowa zmiana ciepła
właściwego
Właściwości termiczne
Ponieważ pary Coopera
nie przekazują energii sieci
krystalicznej:
przewodnictwo cieplne
maleje.
Skokowa zmiana ciepła
właściwego
Diamagnetyzm
Nadprzewodnik jest idealnym diamagnetykiem:
wypycha pole magnetyczne ze swojego wnętrza.
Fenomenologiczny opis własności
magnetycznych: RÓWNANIA LONDONÓW.
Zwykły metal
Nadprzewodnik
Diamagnetyzm
• Zgodnie z definicją namagnesowanie
doskonałego diamagnetyku kompensuje
całkowicie zewnętrzne pole magnetyczne, jest
więc równe
M = −H
gdzie H jest natężeniem zewnętrznego pola
magnetycznego. Odpowiada to zerowej indukcji
magnetycznej wewnątrz materiału.
B = µ 0 (M + H ) = 0
Dwa typy zachowań nadprzewodnika w polu magnetycznym
Pole magnetyczne
magnetisation [emu]
namagnesowanie
0.1
0.0
-0.1
nadprzewodnik
-0.2
Hc
-0.3
-0.4
-0.5
-0.6
-0.7
0
1
2
3
4
5
field [tesla]
Nadprzewodniki I rodzaju: zachowują się w polu magnetycznym tak, ja
to zostało opisane: poniżej pola krytycznego całkowicie wypychaja pole z
wnętrza materiału, powyżej Bc – pole wnika, jak do normalnego metalu.
magnetisation [emu]
0.1
Hc1
0.0
Hc
Hc2
idealny
stan
diamag mieszany
netyk
-0.1
-0.2
stan
normalny
-0.3
-0.4
-0.5
-0.6
-0.7
0
1
2
3
4
5
6
7
8
9
field [tesla]
Nadprzewodniki II rodzaju: W odróżnieniu od nadprzewodników
pierwszego rodzaju, zachowują się one tak, że w pewnym zakresie
pola magnetycz-nego, pole częściowo wnika do wnętrza
nadprzewodnika.
Na czym polega częściowe wnikanie pola
magnetycznego:
„Widok z góry”
Kwant strumienia
pola
magnetycznego
(wir, worteks)
RÓWNANIA LONDONÓW
Z rozwiązania równań Maxwella w przypadku materiału o
zerowym oporze wynika, że w takim materiale zmiany
pola magnetycznego nie przenikają do wnętrza
materiału, tylko zanikają eksponencjalnie:
dB
dB
(x) =
(0)e − x α , gdzie
dt
dt
1
α
=
m
e 2nµ0
Z doświadczenia wiadomo, że w nadprzewodnikach nie
tylko zmiany pola magnetycznego ale również pole
magnetyczne nie wnika do wnętrza nadprzewodnika.
F. i H. Londonowie zaproponowali fenomenologiczny opis
tego zjawiska w taki sposób, że
B( x ) = B(0)e − x α , gdzie
1
α
=
m
2
e nµ0
tzw. londonowską glebokoscia wnikania
≡ λL jest
Na granicy między nadprzewodnikiem a otoczeniem, w
którym B ≠0:
Nadprzewodnik
−
x
B( x ) = B(0)e λ
λ – głębokość wnikania
pola magnetycznego
B AA
B AA exp(− x λ )
x
Nadprzewodnik to nie jest tylko idealny
przewodnik !
Kwantowanie strumienia pola
magnetycznego
Magnetic
field
B
Pierścień
nadprzewodzący
W nadprzewodnikach, strumień pola magnetycznego jest
skwantowany. Kwant strumienia wynosi:
Φ0 = h/2e = 2.07 x 10 -15 weber
Prąd krytyczny, pole krytyczne, głębokość
wnikania pola magnetycznego, temperatura
krytyczna
• Stan nadprzewodzący można zniszczyć
– ogrzewając materiał powyżej temperatury
krytycznej;
– umieszczając go w polu magnetycznym
większym od pola krytycznego;
– gdy płynie prąd krytyczny.
• Pole i prąd krytyczny zależą od temperatury w
podobny sposób:
jc
Normalny
metal
Nadprzewodnik
T
Tc
Mikroskopowa teoria nadprzewodnictwa:
teoria Bardeena Coopera Schrieffera (BCS)
przesłanki:
1.
Pierwszy krok (Frohlich, 1950): oddziaływanie elektronfonon może doprowadzić do przyciągania pomiędzy
elektronami (gdy Ei - Ei jest mniej więcej ωq)
2.
Jeżeli istnieje takie właśnie przyciąganie między
elektronami, to tworzą się pary elektronowe (pary
Coopera)
3.
Nadprzewodnictwo
jest związane z istnieniem
pewnego uporządkowania elektronów
Przyciąganie między elektronami
• W normalnych warunkach, w 0K, gaz elektronów
swobodnych opisywany jest przez model Fermiego,
w którym elektrony zajmują wszystkie stany
energetyczne poniżej poziomu Fermiego. Frölich , a
później Cooper wykazali, że w niskich
temperaturach gaz elektronów Fermiego nie jest
stanem, w którym układ elektronów swobodnych w
ciele stałym ma minimum energii. Okazuje się, że
w sieci krystalicznej istnieje słabe oddziaływanie
przyciągające pomiędzy elektronami, które obniża
energię układu elektronów swobodnych.
Oddziaływanie to wynika z faktu ,że pole
elektryczne ładunku elektronu polaryzuje sieć
krystaliczną. Wytworzony w ten sposób zespół
dipoli elektrycznych, związanych z jonami sieci
wytwarza pole, które przez pozostałe elektrony
„odczuwane” będzie jako przyciągnie.
Bez wzorów:
• Przyczyną powstania nadprzewodnictwa jest jakieś
oddziaływanie pomiędzy elektronami, które
prowadzi do tego, że ELEKTRONY SIĘ
PRZYCIĄGAJĄ.
W konwencjonalnych nadprzewodnikach jest to
oddziaływanie z siecią krystaliczną (oddziaływanie
elektron-fonon).
Główne tezy teorii BCS:
1
W temperaturze, w której wypadkowe oddziaływanie
między elektronami staje się przyciągające, wówczas stan
nieskorelowanych elektronów w morzu Fermiego staje się
niestabilny
zaczynają tworzyć się pary
Coopera. Proces ten trwa tak długo aż energia swobodna
układu osiągnie minimum.
2.
Pary Coopera tworzą te elektrony, które maja takie
wektory falowe ki, że ich energia liczona względem energii
Fermiego :
k i2h 2
εk =
− E F ≤ hωq
2m
Główne tezy teorii BCS:
3.
Przyciąganie miedzy elektronami odbywa się za
pośrednictwem fononów.
4.
Dwa elektrony tworząc parę Coopera (w przypadku
najkorzystniejszym, czyli k i -k ) mają całkowitą energię:E = 2EF - ∆ <
2EF
5.
każda para Coopera ma taką samą energię.
Energia
Swobodne
elektrony
Pary Coopera
Struktura energetyczna nadprzewodnika. Pasmo
odpowiada stanom wzbudzonym pary czyli swobodnym
elektronom
Główne tezy teorii BCS:
prąd krytyczny
• Prąd nadprzewodzący jest spowodowany
ruchem par Coopera .Gęstość prądu:
enh
j = enυ =
K
2m
– K jest wektorem falowym pary Coopera .
– Ruch pary Coopera powoduje przyrost jej
energii kinetycznej . Ten przyrost energii
przypadający na jeden elektron jest równy
∆E =
K 2
)
2
2
2
h
h
(
k
)
kF K
F
2 −
≈
2m
2m
2m
h 2 (kF +
Główne tezy teorii BCS:
prąd krytyczny
– Jeżeli energia kinetyczna pary przekroczy
wartość para samorzutnie ulegnie
rozpadowi. Warunek
h2kF K
≥ 2∆
m
– pozwala na obliczenie krytycznej gęstości
prądu nadprzewodnictwa. Zatem:
en∆
jc =
hk F
Zerowy opór
• Wiemy,że opór metali wynika z oddziaływania
elektronów z drganiami sieci krystalicznej
(następuje zmiana kierunku ruchu elektronu,
czyli ograniczenie prądu elektrycznego).
• W nadprzewodniku oddziaływanie elektronu z
drganiami sieci prowadzi do powstania pary
Coopera.
Elektron zmienia swój pęd, ale para Coopera nie!!!