Wykład X Nadprzewodnictwo

Wykład XI. Nadprzewodnictwo.
Podstawowe definicje
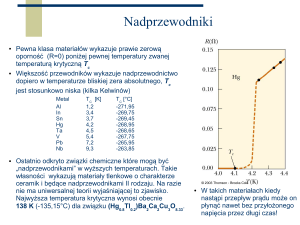
Zjawisko znikania oporu elektrycznego rtęci w temperaturze kilku kelwinów zostało zaobserwowane
po raz pierwszy w 1911 roku przez Kamerlingh’a Onnes’a . Później obserwowano to zjawisko w wielu innych
metalach oraz ich stopach, a w latach osiemdziesiątych w szeregu materiałach niemetalicznych , głównie
tlenkach ziem rzadkich domieszkowanych metalami. Co ciekawe materiały te w warunkach normalnych
bardzo słabo przewodziły prąd elektryczny , zaś zanik oporu elektrycznego występuje w nich już w stosunkowo
wysokich temperaturach kilkudziesięciu kelwinów.
Okazuje się , że w niskich temperaturach oprócz znikania oporu elektrycznego pojawia się szereg
innych ciekawych właściwości ciał, zaś przejście od stanu normalnego do stanu nadprzewodzącego ma wszelkie
cechy przejścia fazowego. Prowadzi to bezpośrednio do wniosku , że mamy tu do czynienia ze specyficznym
stanem układu zwanym stanem nadprzewodzącym. W stanie nadprzewodzącym substancja posiada
następujące cechy:
1.
Opór elektryczny równy jest zeru.
2.
Materiał staje się doskonałym diamagnetykiem .
Określa się temperaturę krytyczną i krytyczne pole magnetyczne, które to parametry odpowiadają
przejściu fazowemu pomiędzy stanem normalnym a stanem nadprzewodzącym. Oznacza to ,że normalny
przewodnik przechodzi do stanu nadprzewodzącego jeśli obniżymy jego temperaturę poniżej temperatury
krytycznej, Tc, Wartość temperatury krytycznej zależy od natężenia zewnętrznego pola magnetycznego ( H c ) i
jest maksymalna w nieobecności pola. Przykładowy diagram fazowy przedstawiony jest na rysunku XI-1a.
Widać, że dla temperatur wyższych od temperatury krytycznej nadprzewodnik przechodzi do stanu normalnego.
Równie ważny jest fakt , że wzrost zewnętrznego pola magnetycznego także powoduje przejście do stanu
normalnego. Wartość krytycznego natężenia pola magnetycznego jest skorelowana z wartością temperatury
krytycznej. Im niższe pole magnetyczne tym wyższa temperatura krytyczna i na odwrót im wyższa temperatura
krytyczna tym niższe natężanie pola krytycznego. Podobny wykres fazowy otrzymuję się gdy zamiast pola
magnetycznego analizujemy prąd płynący w nadprzewodniku. Jeśli prąd wzrośnie powyżej wartości krytycznej
, zależnej od temperatury nadprzewodnik przechodzi do stanu normalnego ( patrz diagram XI-b).
Powróćmy do własności magnetycznych nadprzewodnika. Doskonały diamagnetyzm stanu
nadprzewodzącego zastał odkryty przez Meissnera i Oshenfelda. Zjawisko to nosi nazwę efektu Meissnera –
Oshenfelda. Zgodnie z definicją namagnesowanie doskonałego diamagnetyku kompensuje całkowicie
zewnętrzne pole magnetyczne, jest więc równe
M  H
(XI-1)
gdzie H jest natężeniem zewnętrznego pola magnetycznego. Odpowiada to zerowej indukcji magnetycznej
wewnątrz materiału.
B   0 (M  H )  0
We wzorze (XI-2)
0
(XI-2)
jest przenikalnością magnetyczną próżni. Siły działające na diamagnetyk umieszczony w
polu magnetycznym , kierują go do obszaru o najniższym natężeniu pola. Efekt ten często wykorzystywany jest
w demonstracjach nadprzewodnictwa wysokotemperaturowego , gdzie pokazuje się jak po oziębieniu
1
nadprzewodnik lewituje w polu magnetycznym. Można zmierzyć namagnesowanie w funkcji indukcji
magnetycznej B. Dla materiałów , które są niemagnetyczne w stanie normalnym odpowiednie wykresy
przedstawione są na rysunkach XI-2 a i b.
Rysunek XI-1 a
Zależność natężenia
krytycznego pola
magnetycznego od
temperatury
b zależność prądu
krytycznego od
temperatury. Na
diagramach
zakreskowano
obszar , który
odpowiada stanowi
nadprzewodnictwa.
1000
Stan normalny
a
H (Gs)
500
Stan nadprzewodzący
0
4
8
T (K)
Prąd krytyczny
Stan normalny
b
Stan nadprzewodzący
0
4
8
T (K)
Materiał niemagnetyczny ( doskonały paramagnetyk ) to taki w którym, w stanie normalnym
namagnesowanie jest równe zeru . Rozważmy rysunek( XI-2.a). Począwszy od zera aż do wartości krytycznej
namagnesowanie rośnie wprost proporcjonalnie do wartości indukcji magnetycznej. Jeśli indukcja
wzrośnie powyżej wartości krytycznej materiał ten przechodzi natychmiast ze stanu nadprzewodzącego
do stanu normalnego. Nie istnieje w tym przypadku stan mieszany. Materiał mający taką cechę
nazywamy nadprzewodnikiem I rodzaju .
Na rysunku XI-2 b przedstawiony jest wykres zależności namagnesowania od indukcji dla innego typu
nadprzewodnika . Widzimy, że namagnesowanie początkowo rośnie tak jak poprzednio aż do wartości B kr1
, następnie zaczyna maleć i osiąga wartość zerową, co odpowiada przejściu do stanu normalnego, po
przekroczeniu przez indukcję wartości Bkr2. W zakresie indukcji pomiędzy Bkr1 i Bkr2 mamy do czynienia
ze stanem mieszanym, w którym pewna objętość materiału jest nadprzewodząca a pewna znajduje się już
w stanie normalnym. Materiał taki nazywamy nadprzewodnikiem II rodzaju.
2
Namagnesowanie –μ0M
a
Bkr
Namagnesowanie –μ0M
Rys XI-2 zależność
namagnesowania od pola
magnetycznego dla
nadprzewodnika pierwszego
rodzaju (a) i drugiego
rodzaju (b). W przypadku
nadprzewodnika pierwszego
rodzaju istnieje tylko jedna
wartość pola krytycznego.
W przypadku
nadprzewodnika drugiego
rodzaju istnieją dwie
wartości pola krytycznego
b
Bkr1
Bkr2
Równania Londonów
Spróbujmy rozważyć jakie są konsekwencje zerowej oporności elektrycznej materiału i jakie
wymagania muszą być spełnione aby materiał był idealnym diamagnetykiem. Do analizy oporności można
posłużyć się modelem Drude’go, w którym ruch elektronów wymuszany przez zewnętrzne pole elektryczne
opisuje się równaniem:
m
υ m
 υ u  eε
t 
gdzie
 , u , 
(XI-3)
są odpowiednio prędkością średnią elektronów, prędkością unoszenia i średnim czasem
pomiędzy dwoma rozproszeniami ( zderzeniami z defektami sieci ,fononami , innymi elektronami , itp)
pojedynczego elektronu .Przypomnijmy, że w przypadku klasycznego przewodnictwa średnia prędkość
elektronu nie ulega zmianie, stąd pierwszy człon z lewej strony równania (XI-3) znika, zaś prąd
elektryczny pojawia się ponieważ elektrony poruszają się z prędkością unoszenia. W konsekwencji
otrzymuje się następujące wyrażenie na oporność właściwą przewodnika,

m
e 2n
, gdzie n jest ilością
elektronów. Zgodnie z tym wzorem w przewodniku o zerowej oporności średni czas pomiędzy
zderzeniami elektronów powinien być nieskończony. Elektrony nie będą więc rozpraszane.
Pomijając
dyskusję o przyczynach tak niezwykłego zjawiska ograniczymy się do stwierdzenia ,że brak rozpraszania
prowadzić musi do znikania drugiego członu równania (XI-3). Będzie miało ono teraz postać:
3
m
υ
 eε
t
(XI-4)
Korzystając z definicji gęstości prądu ,
j  neυ
(XI-5)
otrzymujemy równanie opisujące prąd w nadprzewodniku ,
j e 2 n

ε
t
m
(XI-6)
Widać , że w nadprzewodniku nie jest spełnione prawo Ohma. Stałe pole elektryczne nie powoduje przepływu
stałego prądu .
Prąd rośnie w czasie w miarę jak wzrasta średnia prędkość elektronów. Równanie (XI-6) jest
jednym z dwóch równań Londonów. Drugie równanie Londonów opisuje oddziaływanie prądu
nadprzewodnictwa z polem magnetycznym. Podstawiając równanie (XI-6) do równania Maxwella
rotε  
B
t
(XI-7)
otrzymujemy
 m

 2 rotj  B   0
t  ne

(XI-8)
Szczególne rozwiązanie tego równania można otrzymać przy założeniu, że
rotj  
ne 2
B
m
(XI-9)
Równanie (XI-9) jest właśnie drugim równaniem Londonów.
Z równania (XI-9) wynikają własności diamagnetyczne nadprzewodnika. Przyjrzyjmy się rozkładowi pola
magnetycznego w nadprzewodniku nieco dokładniej. Kombinując równania (XI-6) , (XI-9) oraz równanie
Maxwella
rotB   0 j
(XI-10)
otrzymujemy następujące równoważne układy równań
ne 2
B
m
ne 2
rotrotj    0
j
m
rotrotB    0
(XI-11)
lub
ne 2
  B   0
B
m
ne 2
  2 j   0
j
m
2
(XI-12)
Rozwiązania układu równań (XI-12) wygodnie jest dyskutować dla prostego przypadku gdy granica pomiędzy
nadprzewodnikiem i próżnią przebiegaj w płaszczyźnie xy oraz gdy pole magnetyczne skierowane jest wzdłuż
osi x. Patrz Rysunek XI-3 . Aby otrzymać układ równań skorzystano z faktu, że dla pól bezźródłowych
rot  rotB   2 B
4
Bx
X
próżnia
nadprzewodnik
y
Rys. XI. 3 .
półnieskończony
nadprzewodnik
rozciągający się w
kierunku z>0 w polu
magnetycznym
z
Zgodnie z równaniem (XI-9) wewnętrzne pole magnetyczne będzie indukowało gęstość prądu płynącego w
kierunku y. Równia (XI-12) będą miały postać
2
ne 2
Bx   0
Bx
m
z 2
2
ne 2
j



jy
y
0
m
z 2
(XI-13)
Równania (XI-13) mają rozwiązania, które opisują zanik prądu nadprzewodzącego i indukcji magnetycznej
wewnątrz nadprzewodnika.

 0 ne 2 
B x ( z )  B x (0)  exp 
 z
m


(XI-14)

 0 ne 2 
j y ( z )  j y (0)  exp 
 z
m


Widać, że zarówno indukcja jak i prąd nadprzewodzący znika eksponencjalnie wewnątrz nadprzewodnika.
Proces ten opisuje ilościowo charakterystyczna głębokość wnikania
m
  . Dla nadprzewodników
 0 ne 2
metalicznych głębokość wnikania jest równa kilkaset Å.
Należy zwrócić uwagę, że zerowa oporność elektryczna nie jest warunkiem dostatecznym na to aby
materiał był idealnym diamagnetykiem. Z równań Maxwella wynika tylko równanie (XI-8), które mówi, że
jeśli opór elektryczny jest równy zeru to prądy elektryczne i indukcja magnetyczna nie zmieniają się w czasie.
W szczególności suma w nawiasie w równaniu (XI-8) nie musi być równa zeru. W takim materiale pole
magnetyczne i indukowany przez nie prąd nadprzewodzący są niezerowe w całej objętości próbki. Ma to istotne
konsekwencje w przypadku, gdy oziębiamy materiał do temperatury niższej niż temperatura krytyczna w
obecności pola magnetycznego. Jeśli po takim oziębieniu idealnego przewodnika wyłączylibyśmy
zewnętrzne pole magnetyczne to zanik pola zewnętrznego musiały spowodować pojawienie się magnetyzacji
5
materiału. Zjawiska tego nie obserwuje się w realnych nadprzewodnikach.
Zachowanie się przewodnika o
zerowej temperaturze i nadprzewodnika w polu magnetycznym przedstawione jest na rysunku( XI-4)
Fig XI-4
Opis zjawiska nadprzewodnictwa przedstawiony w tym paragrafie ma charakter fenomenologiczny i
nie wyjaśnia dlaczego niektóre materiały w niskich temperaturach mogą przejść do stanu nadprzewodzącego.
W zasadzie w chwili obecnej nie ma spójnego modelu mogącego wyjaśnić nadprzewodnictwo metali oraz
zjawisko nadprzewodnictwa wysokotemperaturowego występującego w nie przewodzących w normalnych
warunkach, w związkach ziem rzadkich.
Znaczącym krokiem w zrozumieniu zjawiska nadprzewodnictwa jest koncepcja par Coopera i teoria
Bardeena Coopera i Schriffera (BCS). Jeśli przyjąć, że opór elektryczny materiału związany jest z
rozpraszaniem elektronów, a brak oporu elektrycznego wynika z możliwości całkowicie swobodnego ruchu
nośników prądu, wyjaśniając fenomen nadprzewodnictwa należy szukać zjawisk, które eliminowałyby lub
ograniczały możliwość rozproszeń pojedynczych elektronów .
6
Mikroskopowy model nadprzewodnictwa. Pary Coopera
W normalnych warunkach, w temperaturze 0K, gaz elektronów swobodnych opisywany jest przez
model Fermiego, w którym elektrony zajmują wszystkie stany energetyczne leżące poniżej poziomu Fermiego.
Frölich , a później Cooper wykazali, że w niskich temperaturach gaz elektronów Fermiego nie jest stanem, w
którym układ elektronów swobodnych w ciele stałym ma minimum energii. Okazuje się, że w sieci
krystalicznej istnieje słabe oddziaływanie przyciągające pomiędzy elektronami, które obniża energię układu
elektronów swobodnych. Oddziaływanie to wynika z faktu ,że pole elektryczne ładunku elektronu polaryzuje
sieć krystaliczną. Wytworzony w ten sposób zespół dipoli elektrycznych, związanych z jonami ( atomami ) sieci
wytwarza potencjał, który przez pozostałe elektrony „odczuwany” będzie jako potencjał przyciągający.
Na ogół rozważa się dwa oddziaływujące ze sobą elektrony. Obiekt taki nazywany jest parą
Coopera. Zgodnie z regułami mechaniki kwantowej energię pary Coopera można obliczyć rozwiązując
następujące równanie Schrödingera.
   2 12   2  22 

 2 k12  2 k 22 



(
r
,
r
)

V
(
r
,
r
)


(
r
,
r
)


E





   (r1 , r2 )
1
2
1
2
1
2
2m 
2m
2m 
 2m

(XI-
15)
 (r1 , r2 ) 
gdzie
 g (k
1
, k 2 ) k 1k 2 (r1 , r2 ) jest dwuelektronową funkcją falową ,zaś  k1k2 (r1 , r2 ) , jest
k 1k 2
dwuelektronową funkcją Blocha, którą można przedstawić przy pomocy iloczynu funkcji jednoelektronowych (
w przypadku modelu swobodnych elektronów będą to odpowiednie fale płaskie, zaś stałe
współczynnikami rozwinięcia.
g (k 1 , k 2 ) są
V (r1 , r2 ) jest potencjałem oddziaływania pomiędzy elektronami. Dokładna
analiza oddziaływania elektronu z siecią krystaliczną, która tu nie zostanie przedstawiona, pozwala stwierdzić,
że wystarczy uwzględniać tylko oddziaływanie pomiędzy elektronami o energiach bliskich energii Fermiego.
Dokładnie, energie elektronów spełniać muszą warunki
EF 
 2 k12  2 k 22
,
 E F   D
2m 2m
gdzie
 D jest energią Debye’a . Co więcej możemy uwzględniać tylko pary, których pędy są przeciwne czyli
takie ,że
(XI-16)
k 1  k 2 . Dla nich potencjał oddziaływania przybliżony jest przez stałą wartość, -V0 . Dla
pozostałych par elektronów potencjał przyciągający jest równy zeru. Nie wchodząc w szczegóły obliczeniowe
podamy przybliżoną wartość energii o którą obniży się energia pary Coopera względem energii dwóch
swobodnych elektronów na powierzchni Fermiego, E
 1 

E  2  D exp 
V 0 Z (k F ) 
gdzie
(XI-17)
Z (k F ) jest powierzchniową gęstością stanów na powierzchni Fermiego. Dla przybliżenia swobodnych
elektronów:
7
Z (k F ) 
mk F
2 2  2
(XI-18)
gdzie kF jest wektorem Fermiego.
Ujemna energia pary Coopera powoduje, że w niskich temperaturach łączenie się elektronów w takie
pary jest korzystne energetycznie.
Jeśli rozpatruje się parę Coopera jako jedna cząstkę zauważamy, że obiekt taki ma spin będący
sumą lub różnicą spinów elektronów, czyli mają wartość 1 lub 0 ( w rzeczywistości spotyka się tylko pary
o spinie zerowym). W obu jednak przypadkach para jest się bozonem, podlega więc statystyce Bosego.
Oznacza to, że nieskończenie wiele par może znajdować się w jednym stanie energetycznym.
Stan podstawowy „gazu” par Coopera. Teoria BCS
Energia wyrażona wzorem (XI-17) jest energią pojedynczej pary elektronów, przy założeniu ,że
pozostałe elektrony nie tworzą par. Jest oczywiste ,że sytuacja taka aczkolwiek możliwa jest pewnym
szczególnym mało prawdopodobnym przypadkiem. W rzeczywistości tworzyć się będzie znacznie więcej
niż jedna para. Każda sytuacja utworzenia się określonej ilości par Coopera jest pewnym szczególnym
przypadkiem naszego układu i odpowiada pewnemu stanowi energetycznemu. Teoria BCS podaje
przepis na obliczenie energii stanu podstawowego układu, czyli stanu, w którym pary Coopera mają
najniższa energię.
Pomimo, że energia układu zależeć będzie głównie od ilości par Coopera zagadnienie to nie
sprowadza się do prostego mnożenia energii pary przez ilość wszystkich par, zgodnie bowiem z relacją ( XI-16)
generacja pary Coopera , poprzez fakt , że na to aby tworzyć parę elektrony muszą zostać wzbudzone ponad
poziom Fermiego, powoduje wzrost energii kinetycznej całego układu
Nie wchodząc w szczegóły podamy tu sposób w jaki zostały przeprowadzone rachunki. Rozważa się
układ elektronów w temperaturze 0K. Do obliczenia energii stanu podstawowego par Coopera użyto
przybliżenia wielocząstkowego , w którym stan układu opisywany był przez funkcję falową będącą iloczynem
jednoelektronowych funkcji falowych pojedynczych par. Przyjęto , że każda z par elektronów o wektorach
falowych k,k może znajdować się w dwóch stanach energetycznych; może istnieć jako para – mamy
wówczas stan |1>- lub może nie istnieć jako para - mamy wówczas stan |0> . Dlatego też funkcja falowa
pojedynczej pary jest kombinacją liniową dwóch składników ( |1> i |0>). W konsekwencji stan układu w teorii
BCS opisuje się przez następującą funkcję:
|  BCS   (a k 1  bk 0 )
(XI-19)
k
2
2
gdzie a k , bk są prawdopodobieństwami, że istnieje lub nie istnieje odpowiednia para Coopera o wektorze
falowym (k, -k). Energię układu , W, można policzyć znajdując wartość oczekiwaną potencjału oddziaływania
pomiędzy elektronami w parze
V , W   BCS V  BCS . Główny problem polega na tym aby przedstawić
potencjał V w odpowiedniej wygodnej formie, jako operator zależny tylko od wektorów falowych. Ponieważ
stan podstawowy ma najniższą energię szuka się minimum energii powyższej całki
8
W 0  min  BCS V  BCS
(XI-20)
Pierwszy stan wzbudzony to stan , w którym liczba par Coopera zmniejszyła się o 1. Znajomość energii
stanu podstawowego pozwala obliczyć energię pierwszego stanu wzbudzonego , czyli energię jaka jest
potrzebna do rozbicia pojedynczej pary. Różnica energii pomiędzy stanem podstawowym W
wzbudzonym W
1
0
a stanem
jest równa
 1 

W 1  W 0    2 D exp 
 V0 Z (k F ) 
(XI-21)
Struktura energetyczna par Coopera przedstawiona jest na rysunku XI-5. Przedstawiono tu energię
przypadająca na jeden elektron. Dyskretny stan podstawowy odpowiada stanowi podstawowemu BCS, czyli
istnienia par Coopera. Aby pojedyncza para została rozbita trzeba dostarczyć do układu energię większą niż
2 .
Energia
Swobodne elektrony
∆
Fig XI-5 Struktura
energetyczna
nadprzewodnika. Pasmo
odpowiada stanom
wzbudzonym pary czyli
swobodnym elektronom
Przedstawione są
energie przypadające
na jeden elektron .
Stan podstawowy BCS
Fakt, że do rozbicia pary Coopera potrzebna jest pewna energia jest odpowiedzialny za brak
rozproszeń par Coopera na domieszkach lub defektach sieci.
Brak rozproszeń par wynika z kwantowej natury zjawiska nadprzewodnictwa. Zauważmy przede
wszystkim, że para Coopera składa się z dwóch elektronów o przeciwnych dobrze określonych pędach . Zgodnie
z zasadą nieoznaczoności jest więc ona obiektem zdelokalizowanym w przestrzeni rzeczywistej. Jeśli rozważa
się możliwość rozproszenia takiego złożonego obiektu ( pary Coopera) na zlokalizowanych defektach sieci to
należy uwzględniać tylko oddziaływanie defektu z poszczególnymi elektronami a nie z parą w całości.
Rozproszenie jednego elektronu z pary wiąże się oczywiście ze zmianą jego pędu , a ponieważ zmienia się pęd
tylko jednego elektronu równość
k 1  k 2 przestaje być spełniona i na skutek zaniku potencjału
przyciągającego para musi się rozpaść. Rozpad pary z kolei wymaga dostarczenia energii 2  . W niskiej
temperaturze nie ma swobodnych fononów , które mogłyby dostarczyć tej energii, tak więc dopóki energia
kinetyczna pary jest mniejsza niż 2  rozproszenia nie są możliwe.
Teoria BCS daje poprawny opis szeregu właściwości nadprzewodników metalicznych . Do takich
właściwości należy istnienie temperatury krytycznej a także krytycznego prądu i pola magnetycznego.
9
Rozważmy na początek skąd bierze się prąd krytyczny , czyli dlaczego przez nadprzewodnik nie może płynąć
prąd o gęstości większej niż wartość krytyczna jc.. Prąd nadprzewodzący jest spowodowany ruchem par Coopera
. Zgodnie z zasadami dynamiki,
j  en 
gęstość prądu może być obliczona ze wzoru
en
K
2m
(XI-22)
gdzie e jest ładunkiem elektronu, a
K

prędkością pary Coopera . K jest wektorem falowym pary Coopera
2 m K
.
jest oczywiście przyrostem pędu pojedynczego elektronu wynikającego z ruchu pary. Ruch

2
pary Coopera powoduje przyrost jej energii kinetycznej . Ten przyrost energii przypadający na jeden elektron
jest równy
E 
K 2
)
2
2
2
2   (k F )   k F K
2m
2m
2m
 2 (k F 
Jeżeli energia kinetyczna pary
(XI-23)
2E przekroczy wartość 2 para samorzutnie ulegnie rozpadowi. Warunek
2kF K
 2
m
(XI-24)
pozwala na obliczenie krytycznej gęstości prądu nadprzewodnictwa. Podstawiając za K wartość obliczoną ze
wzoru (XI-22) otrzymamy
jc 
en
k F
(XI-25)
Znając krytyczną wartość gęstości prądu możemy obliczyć wartość krytycznego natężenia pola
magnetycznego, Hc. Całkowa postać równania Maxwella
 Hdl   jdS
(XI-26)
2rH   jdS
gdzie r jest promieniem drutu nadprzewodzącego, pozwala powiązać prąd płynący w nadprzewodniku z
natężeniem indukowanego przezeń pola magnetycznego. Zakładając zgodnie z relacja (XI-14) , że prąd
nadprzewodzący płynie tylko na powierzchniowej warstwie nadprzewodnika, i że grubość tej warstwy wynosi
 otrzymujemy
2rH  2rj
a stąd
H c  j c   
en
k F
(XI-26)
Powyższe rozważania dotyczą oczywiście temperatury 0K
10
Przeanalizujmy teraz co stanie co stanie się jeśli podniesiemy temperaturę. W temperaturze zera
bezwzględnego jeśli prąd nadprzewodzący był mały układ znajdował się w stanie podstawowym BCS. Jeśli
podniesiemy temperaturę część par zostanie rozerwana a elektrony wzbudzone do pasma elektronów
swobodnych. Jednocześnie zmiana ilości par spowoduje zmniejszenie się energii potrzebnej do rozpadu
następnej pojedynczej pary, do wartości 2(T )  2(T  0) (Znajdujemy się w wyższym stanie
energetycznym BCS). To z kolei zwiększy dodatkowo ilość rozpadających się par. Wraz ze wzrostem
temperatury ilość par wzrasta więc lawinowo i dla temperatury krytycznej, dla której (T )  0 mamy przejście
fazowe nadprzewodnik- metal. Temperaturę, przy której zachodzi to przejście nazywamy temperaturą
krytyczną. Teoria BCS pozwala na obliczenie temperatury krytycznej Wynosi ona :
Tc 
 (T  0)
1.763k B
(XI-27)
11