wyznacz. stos. e/m elektronu

Radosława Nowak
WPPT Fizyka II rok
14.10.98
Ćwiczenie nr 52:
WYZNACZANIE ŁADUNKU WŁAŚCIWEGO ELEKTRONU
Cel ćwiczenia:
Praktyczne zapoznanie się ze zjawiskami ruchu elektronów w polu elektrycznym i
magnetycznym oraz z metodami wyznaczania stosunku e/m elektronu.
Część teoretyczna (Opis zagadnień fizycznych).
Na elektron znajdujący się w polu elektrycznym o natężeniu E działa siła:
Fe  e  E
Praca wykonana przez siłę na dowolnej drodze między punktami 1 i 2 zamienia się na energię
kinetyczną elektronu
2
2
mV 2
1 Fe dl  e1 E  dl  e  U  2
gdzie U - napięcie między punktami 1 i 2.
Stąd prędkość elektronu nabyta w polu elektrycznym
V
2eU
.
m
Na elektron poruszający się z prędkością V w polu magnetycznym o indukcji B działa siła:
r
r
Fm  e(V  B)
Jeśli V  B, to elektron porusza się po łuku okręgu o promieniu r takim, aby
mV 2
mV
,
eVB 
eB 
2
r
Opis układów pomiarowych.
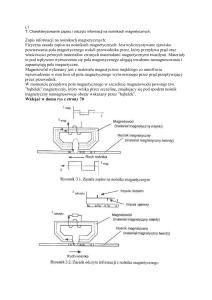
I. Układ do pomiaru e/m metodą poprzecznego pola magnetycznego.
Do wytwarzania wiązki elektronów służy lampa oscyloskopowa. Pole magnetyczne jest
wytwarzane przez cewki Helmholtza (C1,C2), ustawione symetrycznie po obu stronach
lampy. Natężenie prądu I płynącego przez cewki mierzono za pomocą amperomierza A. Pole
elektryczne wytwarza się między płytkami odchylania pionowego lampy oscyloskopowej,
przez przyłożenie napięcia U. Do pomiaru tego napięcia służy woltomierz V.
Po włączeniu zasilania lampy oscyloskopowej i wstępnym wyregulowaniu jasności, ostrości
i położenia zerowego plamki świetlnej na ekranie, włączono prąd do obwodu cewek i
regulując jego natężenie przesunięto plamkę o zadaną wartość y. Następnie przesunięcie to
skompensowano przez doprowadzenie do płytek odchylających odpowiednio dobranej
wartości napięcia U, przy którym plamka powrócił w położenie zerowe. Pomiary wartości I
oraz U wykonano dla kilku wybranych wartości y.
 Wyniki Pomiarów
Wychylenie plamki w dół:
y [cm]
I [mA]
0,5
8,33
1,0
20,00
1,5
33,00
U [V]
9,83
23,00
35,00
Wychylenie plamki w górę:
y [mm]
I [mA]
U [V]
0,5
11,33
11,67
1,0
24,67
24,00
2
1,5
36,17
35,00
II. Układ do pomiaru e/m metodą podłużnego pola magnetycznego.
Urządzenie pomiarowe składa się z lampy oscyloskopowej, umieszczonej współosiowo
wewnątrz solenoidu. Do pomiaru napięcia przyspieszającego służy wbudowany do urządzenia
woltomierz V. Solenoid zasilany prądem stałym z zewnętrznego źródła. Amperomierz A
służy do pomiaru natężenia prądu płynącego przez solenoid. Wewnątrz wytwarzane jest
jednorodne pole magnetyczne o indukcji B, skierowane wzdłuż osi solenoidu. Do płytek
odchylajacych przylożone jest napięcie zmienne.
Na ekranie oscyloskopu jest świecący odcinek (kreska). Po włączeniu prądu w obwodzie
solenoidu i w miarę zwiększania jego natężenia świecący odcinek na ekranie ulega coraz
większemu skręceniu i skróceniu. Przyczyną tego zjawiska jest zmiana torów elektronów z
prostoliniowych na tory spiralne. Regulując natężenie prądu płynącego przez solenoid można
uzyskać zredukowanie śladu wiązki elektronów na ekranie do punktu.
 Wyniki pomiarów
wychylenie poziome(x)
U [V]
I [mA]
900
323,33
1100
330,00
3
1300
1500
328,33
331,67
wychylenie pionowe(y)
U [V]
I [mA]
900
491,67
1100
503,33
1300
525,00
1500
528,33
Część obliczeniowa.
Metoda poprzecznego pola magnetycznego(Thomsona).
DANE:
n= 650 - ilość zwojów w cewce Helmholtza
R= (501) mm - promień cewki
a= (381)mm - połowa odległości pomiędzy cewkami.
d= (4.00.1) mm - odległość płytek odchylających
D= (1001 mm) - średnica obszaru działania pola magnetycznego
L= (901) mm - odległość ekranu od punktu wejścia elektronu w pole magnetyczne
y= 0.5 mm - dokładność odczytu położenia środka plamki
Indukcję magnetyczną B w obszarze środkowym między cewkami Helmholtza obliczono ze
wzoru:
nIR 2
B  0 2
( R  a 2 ) 3/ 2
gdzie:
 0  4  107 Vs/Am - przenikalność magnetyczna próżni ,
I - natężenie prądu [A],
a następnie stosunek e/m ze wzoru:
e
yU
/
 2
m
B dLD
gdzie:
U - napięcie przyłożone do płytek odchylających sprowadzające odchylenie y do
położenia zerowego.
Wyniki obliczeń (metoda Thomsona):
Przesunięcie w dół:
y
[m]
U
[V]
I
[A]
B
[T]
4
e/m
[C/kg]
e/m
[C/kg]
e/m
%
0.005
0.010
0.015
9,83
23,00
35,00
0,00833
0,02000
0,03300
4.855 * 10-4 6.8264*109
11.656*10-4
19.233*10-4
I
[A]
0.01133
0.02467
0.03617
B
e/m
[T]
[C/kg]
6.603 * 10-4 3.7175*109
14.378*10-4
21.080*10-4
Przesunięcie w górę:
y
[m]
0.005
0.010
0.015
U
[V]
11.67
24.00
35.00
e/m
[C/kg]
Dyskusja błędów:
Błąd wyznaczania indukcji B oszacowano na podstawie wzoru
nIR 2
B  0 2
( R  a 2 ) 3/ 2
za pomocą różniczki zupełnej
B
B
B
B 
 I 
 R 
 a
I
R
a
B   0 n
R2
2 R( R 2  a 2 ) 3/ 2  3R 3 ( R 2  a 2 ) 1/ 2

I


nI
 R
0
( R 2  a 2 ) 3/ 2
(R2  a2 )3
5/ 2
 3

  0 nIR 2  R 2  a 2
 2a  a
 2

Błąd względny:
B
B 
B
2a 2  R 2 R
B
I
3a 2 a
B 

 2

B
I
R  a2 R
R2  a2 a
Błąd względny e/m oszacowano za pomocą pochodnej logarytmicznej
 (e / m)
y U
d
L D
 B 




e/ m
y
U
d
L
D
a błąd bezwzględny ze wzoru
 e
 e e
      
 m
 m m


Metoda podłużnego pola magnetycznego.
DANE:
n/b=(720050) zw/m - liczba zwojów na jednostkę długości solenoidu
lx=(22,10.1) cm
5
e/m
%
ly=(18,30.1) cm - odległości płytek odchylających od ekranu
Indukcję magnetyczną B pola magnetycznego skierowanego wzdłuż osi solenoidu
wyznaczono ze wzoru:
n
B  0 I
b
Stosunek e/m ze wzoru:
e 8 2U
0.5U
 2 2 
 1014 [C / kg ]
2
m l B
 n
l2   I 2
 b
Wyniki obliczeń (metoda podłużnego pola):
Wychylenie poziome (x):
U
[V]
900
1100
1300
1500
I
[A]
0.32333
0.33000
0.32833
0.33167
e/m
[C/kg]
e/m
[C/kg]
(e/m)
%
e/m
[C/kg]
e/m
[C/kg]
(e/m)
%
wychylenie pionowe (y):
l y = 0.183 m
U
[V]
900
1100
1300
1500
I
[A]
0.49167
0.50333
0.52500
0.52833
Dyskusja błędów
6
e

m
0.5  U
2
 n
l2   I 2
 b
e / m
e/ m

e / m  
U  
 1014
n / b
U
l
I
2
2
2
;
U
l
n/b
I
e / m e

e/ m m
klasa  zakres
15
.  1500

 22.5V
100
100
Wnioski i uwagi.
Metoda podłużnego pola magnetycznego jest dokładna, ponieważ wielkości:
 napięcie przyspieszające elektrony w lampie oscyloskopowej U
 indukcję pola magnetycznego w solenoidzie B
 odległość płytek odchylających od ekranu lampy L
można dokładnie zmierzyć. Jednorodność pola magnetycznego w środku solenoidu, gdzie
znajduje się lampa oscyloskopowa, też może być duża.
Metoda Thomsona wymaga spełnienia warunków:
 poprzeczne pole magnetyczne powinno występować tylko w kołowym obszarze o średnicy
D
 średnica obszaru D powinna być mała w porównaniu z odległością tego obszaru od ekranu
lampy oscyloskopowej
 pole magnetyczne (indukcja B) powinno być w obszarze o średnicy D jednorodne.
Pole wytworzone w cewkach Helmholtza nie spełnia dokładnie tych wymagań.
Na sześć wykonanych pomiarów e/m metodą Thomsona tylko dwa odpowiadają wartości
rzeczywistej e/m (e/m = 1.7588 1011 ) w granicy oszacowanego błędu.
Przy zastosowaniu metody pola podłużnego otrzymano też zaledwie dwa wyniki na osiem
pomiarów zgodne w granicach oszacowanego błędu z wartością rzeczywistą e/m.
Zależność wyników od odchylenia plamki (metoda Thomsona) i od napięcia
przyspieszającego (metoda pola podłużnego) świadczy o niejednorodności pola
magnetycznego w przestrzeni lampy. W przypadku metody Thomsona pole magnetyczne w
pobliżu osi cewek było wyraźnie większe niż w pozostałym obszarze działania pola. W
metodzie poprzecznego pola natomiast pole magnetyczne malało przy zbliżaniu się do osi
solenoidu.
7