Nadprzewodnictwo
Marek Gieniec IS2R2
Plan prezentacji
Historia
Materiały nadprzewodzące
Własności nadprzewodników
Teoria nadprzewodnictwa
Zastosowania
Perspektywy rozwoju
Historia
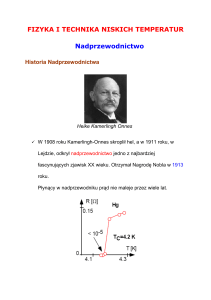
1911 rok – Heike Kamerlingh
Onnes podczas badań
rezystancji rtęci w ciekłym
helu (4,2 K) odkrył
nadprzewodnictwo. Nagroda
nobla 1913 r.
Opór R=0 poniżej TC;
(R<10-23 cm, 1018-razy
mniejsze niż dla Cu)
• 1930 zbadano temperaturę krytyczną Niobu - 9,2 K.
• 1933 Walther Meissner i Robert Ochsenfeld – odkrywają zjawisko
usuwania z wnętrza nadprzewodników pola magnetycznego
• 1935 – bracia Fritz i Heinz Londonowie stworzyli w celu
wytłumaczenia efektu Meissnera- Oschenfelda model Londonów
• 1950 – Vitalij Ginzburg i Lew Landau zaproponowali
fenomenologiczną teorię nadprzewodnictwa
• 1957 – Leon Cooper i Robert Schriefer zaproponowali pełną teorię
nadprzewodnictwa – teorię BCS
• 1962 – Brian Josephson przewidział zjawiska kwantowe zachodzące
w złączach Josephsona
• 1973 – Niskotemperaturowy nadprzewodnik o najwyższej
temperaturze krytycznej 23,2K dla Nb3Ge
• 1986 – Pierwszy wysokotemperaturowy nadprzewodnik (LaBa)2
CuO4 TC=35K
• 1987 (Styczeń): YBa2Cu3O7-x TC=93K
• 1993: Hg-Ba-Ca-Cu-O TC=133K (A. Schilling, H. Ott, ETH Zürich)
Temperatury krytyczne niektórych
pierwiastków
Al (Glin)
Tc(K) = 1,2
In (Ind)
Tc(K) = 3,4
Sn (Cyna)
Tc(K) = 3,7
Hg (Rtęć)
Tc(K) = 4,2
Ta (Tantal)
Tc(K) = 4,5
V (Wanad)
Tc(K) = 5,4
Pb (Ołów)
Tc(K) = 7,2
Nb (Niob)
Tc(K) = 9,3
Pierwiastki nadprzewodzące
Li
Be
K
Rb
Cs
Mg
Ca
Sr
Ba
(Żelazo)
Tc=1K
(@ 20GPa)
(Niob)
0.026
Na
Fe
Nb
Tc=9,5K
Hc=0.2T
Sc
Y
Ti
V
0.39
10
5.38
142
Cr
Mn
Fe
Co
Ni
B
C
N
O
F
Ne
Al
Si
P
S
Cl
Ar
Ge
As
Se
Br
Kr
Sb
Te
I
Xe
Bi
Po
At
Rn
1.14
10
Cu
Zn
Ga
0.875 1.091
5.3
5.1
Zr
Nb
Mo
Tc
Ru
Rh
0.546
4.7
9.5
198
0.92
9.5
7.77
141
0.51
7
0.03
5
La
Hf
Ta
W
Re
Os
Ir
6.0
110
0.12
1.4
20
0.655
16.5
0.14
1.9
4.483 0.012
83
0.1
Pd
Pt
Ag
Au
Cd
In
Sn
0.56
3
3.4
29.3
3.72
30
Hg
Tl
Pb
4.153
41
2.39
17
7.19
80
Temperatury krytyczne nadprzewodzących związków
niskotemperaturowych
V3Si
Nb3Al
Nb3Sn
Nb3Ge
Tc(K) = 15,7
Tc(K) = 16
Tc(K) = 18,3
Tc(K) = 23,2
Wysokotemperaturowych
(La2-xSrx)CuO4
YBa2CuO7-x
HgBa2CuO4
Tl2Ba2CaCu2O8
Bi2Sr3Ca2Cu3O10
HgBa2Ca2Cu3O8
Tc(K) = 36
Tc(K) = 91
Tc(K) = 94
Tc(K) = 80
Tc(K) = 125
Tc(K) = 135
Inne nadprzewodniki
Fizycy poszukiwali nadprzewodników, także wśród
niskowymiarowych związków organicznych.
Nadprzewodnik
(TMTSF)2ClO4
Tc(K)
1,4
(BEDT-TTF)2I3
(BEDT-TTF)2Cu(SCN)2
8,1
10,4
TMTSF – tetrametylotetraselenofulwalen
BEDT-TTF - tetratiometylotetratiofulwalen
Inne nadprzewodniki
Odkryto również nadprzewodnictwo w materiałach
opartych na bazie sześćdziesięcioatomowych cząstek
węgla C60 fulerenów domieszkowanych z metalami
alkalicznymi.
nadprzewodnik
Tc(K)
K3C60
Rb2KC60
Rb3C60
Rb2CsC60
20
25
29
31
Fazy Chevrela
chalkogenki molibdenu o
wzorze
ogólnym MxMoX6, gdzie M jest
pierwiastkiem ziem rzadkich, a
X jest
pierwiastkiem
chalkogenicznym.
Bardzo wysokie wartości krytyczne pól, ale bardzo
krucha budowa i rzadkość występowania pierwiastków.
Nb3Ge
YBa2CuO7-x
najlepiejj poznany nadprzewodnik
wysokotemperaturowy
• Gęstość: g=6,388 g/cm3.
• Stałe sieci: a=0,38929 nm, b=0,38213 nm, c=1,169 nm.
• Podobnie jak we wszystkich nadprzewodnikach
wysokotemperaturowych struktura warstwowa.
• Dla x od 0,5 do 0 struktura rombowa
tylko ta faza jest nadprzewodząca!!!
Przepis na nadprzewodnik
• Weź Y2O3 (tlenek Itru) BaCO3(węglan baru) i CuO masę w
proporcji ½ mola Y2O3, 2 mole BaCO3, 3 mole CuO.
• Trzy wymienione składniki należy rozgnieść i wymieszać w
moździerzu.
• Mieszaninę wsypać do tygielka, przykryć i ogrzewać 10-12
godzin w temperaturze 950 C.
• Powstała substancja powinna mieć czarny kolor. Po
ochłodzeniu materiał ponownie rozdrobić i prasować w pastylki
w temperaturze 900-950 C w ciągu 12-16 godzin pod
ciśnieniem 150 Mpa. A następnie wolno ochładza w atmosferze
tlenowej.
• Ochładzanie powinno się odbywać z prędkością 100C/h.
„Wypychanie pola magnetycznego”
Drugą cechą charakteryzująca nadprzewodniki jest zdolność
do wypychania pola magnetycznego ze swojego wnętrza.
Mówimy, że nadprzewodnik jest idealnym Diamagnetykiem (Efekt
Meissnera) umieszczony w polu magnetycznym wytwarza w
swoim wnętrzu pole przeciwne do pola zewnętrznego.
Stan normaly
Stan nadprzewodzący
Idealny diamagnetyzm
(efekt Meissnera)
Prąd ekranujący na
Powierzchni kuli
wytwarza
przeciwne pole
magnetyczne
A tak to działa
w praktyce
Podział nadprzewodników
I rodzaju
II rodzaju
• Stosunkowo niskie
• Wyższe temperatury
temperatury krytyczne;
krytyczne;
• Związki pierwiastków
• Problemy z innymi
nadprzewodzących;
właściwościami;
• Jedna określona wartość • Dwie wartości krytyczne
krytyczna Hc.
Hc1 i Hc2
Ruch wirów w nadprzewodnikach
II rodzaju
Substancja dalej nadprzewodząca poza nitkami wewnątrz wirów, przez które
przechodzi pole magnetyczne.
Wiry oddziałują z zewnętrznym polem, działa na nie siła Lorenza powodująca ich
ruch.
FL=J X B
Zjawisko to jest bardzo szkodliwe w praktycznych zastosowaniach, gdyż
zmniejsza gęstość prądu krytycznego.
Przewodnictwo
•Sieć dodatnich jonów wypełnia gaz elektronowy;
•Jeśli na układ będziemy oddziaływać, zewnętrznym
polem elektrycznym, to popłynie prąd;
•Temperaturowa zależność przewodnictwa:
ρ=ρi+ρk(T)
• W temperaturze T = 0 K
maksymalną energię elektronu
wewnątrz metalu nazywamy energią
Fermiego
ħ – stała Plancka h, dzielona przez 2π
m – masa elektronów
Teoria nadprzewodnictwa
• Nośniki prądu – Pary elektronów
(pary Coopera);
Pary Coopera, to Bozony. W
przeciwieństwie do Fermionów, nie
obowiązuje zakaz Pauliego.
KONDENSACJA BOSEGO-EINSTEINA
Prawdopodobieństwo, że do grupy
cząstek w pewnym stanie dojdą
kolejne, jest tym większe im więcej
cząstek już w tym stanie przebywa.
Jak powstają pary Coopera?
Elektron przybliża jon dodatni tworząc fonon.
Naładowany dodatnio region przyciąga elektron.
Częstotliwość fononu jest bardzo duża. Siła
odpychania między elektronami jest nie
odczuwalna!
dlaczego pary Coopera nadprzewodzą?
Sumaryczny spin i pęd p-c jest równy 0, co odpowiada fali o nieskończonej
długości, a ta może się załamywać jedynie na obiektach podobnej wielkości do
długości fali. Ponadto Istnienie w parze 2 elektronów z energetycznego punktu
widzenia jest korzystniejsze od niezależnego trwania!
DLATEGO
Pomimo zderzeń np. z defektami sieci pary Coopera,
w przeciwieństwie do pojedynczych elektronów nie
są rozpraszane !!!
Wyjaśnienie efektu Meissnera-Ochsenfelda
E = ρ⋅J | ρ = 0 => E=0.
Z równania Maxwella:
Stąd: B = const
Równania Londonów
• Bracia Londonowie pierwsi opisali zanik oporu.
I równanie Londonów
me
E
J J s
2 s
t ns q
t
me
2 J s B B1
ns q
E B / t
me
2 J s B 0
t ns q
W nadprzewodnikach B=m0H
0ns q 2
Js
H
me
II równanie Londonów
1
me
J s 2 H gdzie L
L
0ns q 2
Skąd
- Londonowska głębokość
wnikania pola H
Pole krytyczne i prąd krytyczny
Hc(T)=Hc(0)(1-(T/Tc)^2)
Podział Zastosowań
•Silnoprądowe
• Elektronika bardzo
słabych sygnałów
ZASTOSOWANIA
Kable nadprzewodzące
Nadprzewodzące elektromagnesy
Lewitacja
Własności nadprzewodników
• Nadprzewodnictwo jest zarówno własnością
elektryczną i magnetyczną ciała stałego.
=n0
0=h/2e=2*10-15Wb
S=1mm2B=2*10-9T
• Podstawowe własności:
– Zanik oporu elektrycznego;
– Spadek podatności magnetycznej;
– Wystąpienie absorpcji mikrofalowej;
Złącza Josephsona
Połączenie dwóch
nadprzewodników
izolatorem
I=I1 sin φ – Natężenie prądu tunelującego przez
złącze Josephsona.
Złącza Josephsona mają zastosowania przy wykrywaniu
bardzo małych
pól magnetycznych (SQUID – magnetografia) a także w
przełączaniu
układu. Są około 1000 razy szybsze niż układy krzemowe.
SQUID
SQUID (Superconducting Quantum
Interference Device) jest
urządzeniem pozwalającym wykrywać
najmniejsze zmiany pola
magnetycznego.
SQUID zbudowany jest z
nadprzewodzącej pętli w
której znajdują się dwa złącza
Josephsona. Złącze to potrafi
wykryć minimalne zmiany
pola magnetycznego i
wytwarza ono dodatkowe
natężenie. Jego analiza może
pomóc w zanalizowaniu pola
magnetycznego
V
-2
-1
/
1
2
Czułość
10V/0
SQUID - Zastosowanie
SQUID-y są bardzo często stosowane w medycynie, zwłaszcza w
magnetografii i magnetokardiografi. Pozwala on na poznanie zasady
działania serce, oraz co ciekawsze naszego mózgu (SQUID pozwala
zaobserwować zjawiska dziejące się w mózgu a nie jego budowę).
Badania te są nieocenione we współczesnej medycynie.
Inne zastosowania:
• Meteorologia (SQUID);
• DC-SQUID;
• Transformatory strumienia
magnetycznego;
• Supertrony;
• Łożyska nadprzewodzące;
• Technika obliczeniowa;
• Mikrofalowe rezonatory;
• Nadprzewodzące komputery
kwantowe;
Nowinki
• Pierwszy tranzystor cieplny (Heat transistor);
• 175 K – Nowy rekord temperatury krytycznej,
dla Sn1.4In0.6Ba4Tm5Cu7O20+ ;
• NASA otrzymała 400 mln USD na nowe
nadprzewodzące komponenty komputerowe,
nadprzewodzący procesor ma działać 1000
razy szybciej;
Bibliografia
• Michel Cyrot, Davor Pavuna - Wstęp do
Nadprzewodnictwa, PWN 1996 Warszawa
• Jan Stankowski, Borysław Czyżak –
Nadprzewodnictwo, WNT 1999 Warszawa
• Stefan Janiczek – Podstawy
Krioelektrotechniki, Politechnika
Częstochowska 1993 Częstochowa.