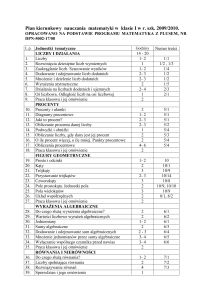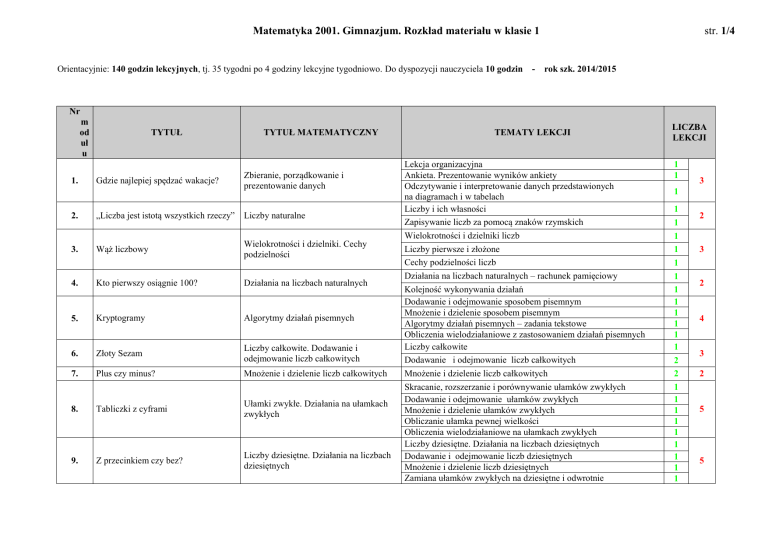
Matematyka 2001. Gimnazjum. Rozkład materiału w klasie 1
Orientacyjnie: 140 godzin lekcyjnych, tj. 35 tygodni po 4 godziny lekcyjne tygodniowo. Do dyspozycji nauczyciela 10 godzin
-
str. 1/4
rok szk. 2014/2015
Nr
m
od
uł
u
1.
TYTUŁ
Gdzie najlepiej spędzać wakacje?
TYTUŁ MATEMATYCZNY
Zbieranie, porządkowanie i
prezentowanie danych
2.
„Liczba jest istotą wszystkich rzeczy”
Liczby naturalne
3.
Wąż liczbowy
Wielokrotności i dzielniki. Cechy
podzielności
4.
Kto pierwszy osiągnie 100?
Działania na liczbach naturalnych
5.
Kryptogramy
Algorytmy działań pisemnych
6.
Złoty Sezam
Liczby całkowite. Dodawanie i
odejmowanie liczb całkowitych
7.
Plus czy minus?
Mnożenie i dzielenie liczb całkowitych
8.
Tabliczki z cyframi
Ułamki zwykłe. Działania na ułamkach
zwykłych
9.
Z przecinkiem czy bez?
Liczby dziesiętne. Działania na liczbach
dziesiętnych
TEMATY LEKCJI
Lekcja organizacyjna
Ankieta. Prezentowanie wyników ankiety
Odczytywanie i interpretowanie danych przedstawionych
na diagramach i w tabelach
Liczby i ich własności
Zapisywanie liczb za pomocą znaków rzymskich
Wielokrotności i dzielniki liczb
Liczby pierwsze i złożone
Cechy podzielności liczb
Działania na liczbach naturalnych – rachunek pamięciowy
Kolejność wykonywania działań
Dodawanie i odejmowanie sposobem pisemnym
Mnożenie i dzielenie sposobem pisemnym
Algorytmy działań pisemnych – zadania tekstowe
Obliczenia wielodziałaniowe z zastosowaniem działań pisemnych
Liczby całkowite
Dodawanie i odejmowanie liczb całkowitych
Mnożenie i dzielenie liczb całkowitych
Skracanie, rozszerzanie i porównywanie ułamków zwykłych
Dodawanie i odejmowanie ułamków zwykłych
Mnożenie i dzielenie ułamków zwykłych
Obliczanie ułamka pewnej wielkości
Obliczenia wielodziałaniowe na ułamkach zwykłych
Liczby dziesiętne. Działania na liczbach dziesiętnych
Dodawanie i odejmowanie liczb dziesiętnych
Mnożenie i dzielenie liczb dziesiętnych
Zamiana ułamków zwykłych na dziesiętne i odwrotnie
LICZBA
LEKCJI
1
1
3
1
1
1
1
1
1
1
1
1
1
1
1
1
2
2
1
1
1
1
1
1
1
1
1
2
3
2
4
3
2
5
5
Matematyka 2001. Gimnazjum. Rozkład materiału w klasie 1
str. 2/4
Nr
m
od
uł
u
10.
TYTUŁ
Pomyśl, oblicz, sprawdź!
Ile ich jest?
11.
TYTUŁ MATEMATYCZNY
Rozwiązywanie zadań tekstowych
Potęgi
Trening przed klasówką nr 1
Praca klasowa nr 1
Poprawa pracy klasowej
12.
„Niech nie wchodzi tu nikt, kto nie
zna geometrii”
Wprowadzenie do geometrii
13.
Zapałczane trójkąty
Własności trójkątów
14.
Panowie i Panie, czas na układanie!
Własności czworokątów
15.
Tyle kątów, ile boków
Własności wielokątów
16.
Dookoła koła
Własności kół i okręgów
17.
Bryły, bryłki
Własności graniastosłupów
18.
Panowie i Panie, czas na budowanie!
Pola powierzchni i objętości
graniastosłupów
Przekroję i zobaczę
19.
Trening przed klasówką nr 2
Praca klasowa nr 2
Poprawa pracy klasowej
Przekroje brył
20.
Gra w statki
Układ współrzędnych
TEMATY LEKCJI
Działania na liczbach dziesiętnych i ułamkach zwykłych
Rozwiązywanie zadań tekstowych
Potęga o wykładniku naturalnym
Własności potęg
Trening przed klasówką nr 1
Praca klasowa nr 1
Poprawa pracy klasowej
Położenie prostych i odcinków na płaszczyźnie
Rodzaje kątów
Kąty przyległe, wierzchołkowe, naprzemianległe i odpowiadające
Własności trójkątów
Pole trójkąta . Obliczanie pola i obwodu trójkąta
Podział czworokątów
Własności czworokątów
Obliczanie pól czworokątów
Własności wielokątów – zastosowanie w zadaniach
Koło i okrąg – wzajemne położenie dwóch okręgów
Położenie dwóch okręgów –zastosowanie w zadaniach
Rodzaje graniastosłupów i ich opisy
Rysowanie siatek i modeli graniastosłupów.
Pole powierzchni i objętość graniastosłupa
Rozwiązywanie zadań – pola powierzchni i objętości graniastosłupów
Przekroje brył
Graniastosłupy i ich przekroje
Trening przed klasówką nr 2
Praca klasowa nr 2
Poprawa pracy klasowej
Prostokątny układ współrzędnych
Położenie punktów w układzie współrzędnych
Zaznaczanie punktów w układzie współrzędnych o danych
własnościach
LICZBA
LEKCJI
1
4
1
1
2
1
1
1
1
1
1
2
1
1
2
2
1
1
1
1
2
1
1
1
2
1
1
1
1
1
4
6
3
3
4
2
2
2
3
6
3
Matematyka 2001. Gimnazjum. Rozkład materiału w klasie 1
str. 3/4
Nr
m
od
uł
u
TYTUŁ
TYTUŁ MATEMATYCZNY
21.
Dawne jednostki – czyli, ile wypijał
imć Zagłoba
Wyrażenia algebraiczne
22.
Suma iloczynów czy iloczyn sum?
Przekształcanie wyrażeń algebraicznych
23.
W poszukiwaniu niewiadomej
Równania stopnia pierwszego z jedną
niewiadomą
24.
Trzy zadania
Nierówności stopnia pierwszego z jedną
niewiadomą
Starszy czy młodszy?
25.
Trening przed klasówką nr 3
Praca klasowa nr 3
Poprawa pracy klasowej
26.
Po drugiej stronie osi
Symetria osiowa. Figury
osiowosymetryczne
27.
Z szyfrem w symetrię środkową
Symetria środkowa. Figury
środkowosymetryczne
Zadania tekstowe
Wielo-rybki
28.
Trening przed klasówką nr 4
Praca klasowa nr 4
Poprawa pracy klasowej
Figury przystające
29.
Na tle innych
Procent liczby
TEMATY LEKCJI
LICZBA
LEKCJI
Wyrażenia algebraiczne. Czytanie i zapisywanie wyrażeń
1
Redukcja wyrazów podobnych
Obliczanie wartości liczbowej wyrażeń algebraicznych
Mnożenie sumy algebraicznej przez jednomian
Wyłączanie wspólnego czynnika przed nawias
Przekształcanie wyrażeń algebraicznych
Opisywanie sytuacji za pomocą równania
Równania równoważne
Rozwiązywanie równań stopnia I z jedną niewiadomą
Opisywanie sytuacji za pomocą nierówności
Ilustracja graficzna nierówności
Jak rozwiązuje się zadania tekstowe za pomocą równań?
Rozwiązywanie zadań tekstowych za pomocą równań
Trening przed klasówką nr 3
Praca klasowa nr 3
Poprawa pracy klasowej
Symetria osiowa
Rozpoznawanie figur symetrycznych
Przekształcanie figur w symetrii osiowej
Figury osiowosymetryczne
Symetria środkowa
Figury środkowosymetryczne
Figury przystające
Cechy przystawania trójkątów
Trening przed klasówką nr 4
Praca klasowa nr 4
Poprawa pracy klasowej
Procent, obliczanie procentu danej liczby
Obliczanie procentu danej liczby, rozwiązywanie zadań tekstowych.
Promil
1
1
1
1
2
1
1
3
1
1
1
3
2
1
1
1
1
1
1
1
1
1
1
2
1
1
1
2
5
2
5
2
8
4
2
6
3
Matematyka 2001. Gimnazjum. Rozkład materiału w klasie 1
str. 4/4
Nr
m
od
uł
u
30.
31.
TYTUŁ
Ile to jest 100%?
Ile złota jest w złocie?
TYTUŁ MATEMATYCZNY
Obliczanie liczby na podstawie jej
procentu
Obliczanie, ile procent jednej liczby
stanowi druga liczba
Czytanka 4. Jak działa bank?
32.
Idealne proporcje
Wielkości proporcjonalne
Diagram Diany
Diagramy kołowe
33.
Trening przed klasówką nr 5
Praca klasowa nr 5
Poprawa pracy klasowej
34.
35.
Prognoza ludności
Czy Czarek jest cwany?
Czytanie wykresów
Badanie sytuacji losowych
Rozkład ten realizują nauczycie uczący matematyki w klasach pierwszych
LICZBA
LEKCJI
TEMATY LEKCJI
Obliczanie liczby, gdy dany jest jej procent
1
Obliczanie liczby, gdy dany jest jej procent – rozwiązywanie zadań
tekstowych
Część z całości – ile to procent?
Obliczanie, ile procent jednej liczby stanowi druga liczba –
rozwiązywanie zadań tekstowych
Wykorzystywanie obliczeń procentowych
Wielkości proporcjonalne – przykłady
Wyznaczanie wielkości proporcjonalnych do danych
Opisywanie proporcji za pomocą ilorazu lub ułamka
Diagramy kołowe
Przedstawianie danych na diagramach kołowych
Odczytywanie i interpretowanie danych przedstawionych
na diagramach kołowych
Trening przed klasówką nr 5
Praca klasowa nr 5
Poprawa pracy klasowej
Odczytywanie wykresów
Odczytywanie i interpretowanie danych przedstawionych
na wykresach
Przykłady doświadczeń losowych
Doświadczenia losowe. Zdarzenia losowe
Zdarzenia: pewne, prawdopodobne, niemożliwe
3
2
1
1
2
1
1
1
1
1
1
2
2
3
7
2
1
1
1
1
1
1
1
Razem 126
2
3
126