Śladami Pitagorejczyków

Śladami
Pitagorejczyków
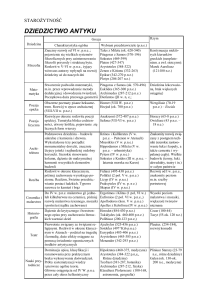
Spis treści
• Demokracja i jej wpływ na kształtowanie się filozofii
• Pitagoras z Samos
• Szkoła Pitagorejska
• Odkrycia matematyczne Pitagorasa i jego szkoły
• Dalsze zdobycze matematyczne pitagorejczyków oraz ich zastosowanie w
życiu codziennym
• Ciekawostki
• Filozofowie matematycy i ich osiągnięcia
• Bibliografia
Demokracja i jej wpływ na
kształtowanie się filozofii
Mimo tego, iż za kolebkę demokracji uważane są Ateny, ustrój ten szybko
znalazł zwolenników w całej Helladzie.
Forma rządów, w której pełnoprawni obywatele czynnie uczestniczyli w
życiu publicznym i mieli na niego duży wpływ, oraz to, iż nie byli obciążani
nadmierną pracą, przyczyniła się do rozwoju szeroko pojętej kultury antycznej.
W tych sprzyjających warunkach zaczęli pojawiać się pierwsi myśliciele, którzy
zastanawiali się nad zagadkami wszechświata. Tak tez narodziła się filozofia,
czyli z greckiego poszukiwanie i umiłowanie mądrości.
Pitagoras z Samos
Pitagoras urodził się w VI w. p.n.e. na wyspie Samos
jako syn grawera Mnesarchosa, pochodzącego z okolic
fenickiego wówczas Tyru. Dokładne ustalenie jego daty
urodzenia przysparza historykom wielu problemów.
Według niektórych źródeł żył on 81 lat, a według innych
104 lata. Przekazy o jego życiu zawierają bardzo dużo treści
legendarnych i jest ich niewiele, dlatego można nawet
wątpić, czy Pitagoras był postacią historyczną. Wszystko co
wiadomo o jego życiu pochodzi od Diogenesa Laertiosa
żyjącego w III w. naszej ery oraz z Żywotów Pitagorasa
napisanych przez Jamblichosa i Porfiriusza na przełomie III
i IV wieku. Przypisuje mu się podróże do Egiptu i
Babilonii, gdzie miał zapoznać się z tamtejszą matematyką,
jednak powoływanie się na wiedzę Egiptu i Babilonii było
w starożytności częstym zabiegiem mającym zwiększyć
wiarygodność danego mistrza. Sam Pitagoras podobno
mówił, że w Egipcie żyją mędrcy, a on jest tylko filozofem
(czyli miłośnikiem wiedzy). W ten sposób Pitagoras
wprowadził określenie filozof.
Szkoła Pitagorejska
Pitagoras założył ją ok. 532 r. p.n.e. po przybyciu do Krotony.
Członkowie szkoły traktowali filozofa jak bóstwo, sami zaś tworzyli
wspólnotę na kształt bractwa, w którym poszczególni członkowie byli
anonimowi, a swoje odkrycia uważali za wspólne dobro, strzegli go i
udostępniali tylko „wtajemniczonym”. Tak zwane „uliczne
filozofowanie” było przez nich uważane za nieprzyzwoite.
Pitagorejczycy prowadzili życie w ascezie, twierdzili bowiem, że
oczyszcza ona ciało a to pozwala panować duszy nad cielesnością. Inna
drogą do oczyszczenia była według nich nauka, często koncentrowali się
na muzyce na jej podstawie nauczano teorii liczb.
Według ich nauczania pierwszymi dwoma zasadami był : bezkres czyli
cos nieograniczonego oraz granica. To założenie dawało początek
rozumowaniu że cały świat działa na zasadzie przeciwieństw i jest
uporządkowany.
Nauczali, że jeśli świat jest harmonijny to można go przedstawić za
pomocą liczb. To założenie powodowało, że postrzegali liczbę jako czynnik
decydujący o własnościach rzeczy. Na pytanie co jest czynnikiem
decydującym o powstawaniu świata odpowiadali : liczba, która zapewnia
mu ład. Uznawali też, że wszystko można przedstawić za pomocą liczb.
Pitagorejczycy jako pierwsi zajmowali się matematyką, mieli niewątpliwie
ogromny wpływ na rozwój i opracowywanie naukowe tej dziedziny , która
dotychczas pozostawała w sferze praktycznej. Najpierw rozważali zasady,
a potem przystępowali do udowadniania ich .
Przypuszcza się, że Pitagoras miał wpływ raczej na filozoficznoreligijną sferę działalności pitagorejczyków, a w rzeczywistości to jego
uczniowie dokonali i udowodnili większości odkryć, które dziś
przypisujemy jemu. Szkoła pitagorasa przetrwała ok. 100 lat. Do
pitagorejczyków mogli dołączyć zarówno mężczyźni jak i kobiety musieli
oni jednak przetrwać pięcioletni okres próby. Po śmierci swojego mędrca
pitagorejczycy podzielili się na tych którzy zajęli się nauką ( matematycy) i
tych którzy poświęcili się działalności religijnej (akuzmatycy). Przyczyną
podziału było prawdopodobnie odkrycie liczb niewymiernych.
WIERZENIA SZKOŁY PITAGOREJSKIEJ:
1. Istnienie duszy i ciała jako odrębnych części człowieka.
2. Możliwość wejścia duszy w ciało.
3. Wyższość duszy nad ciałem.
4. Ciało jako więzienie duszy
5. Istnienie duszy w ciele jest karą za popełnione winy.
6. Celem życia jest wyzwolenie duszy i możliwość
wyzwolenia duszy przez praktyki religijne.
Odkrycia matematyczne
Pitagorasa i jego szkoły
1. Teoria równoległych wspólnie z twierdzeniem
o sumie kątów w trójkącie
Nie znany jest sposób dowodzenia tego twierdzenia przez Pitagorasa.
Prawdopodobnie dowodził on to twierdzenie przez uzupełnienie do
prostokątów trójkątów prostokątnych. Można przypuszczać, że zauważył, iż
każdy trójkąt można podzielić prostopadłą opuszczoną z wierzchołka na
dwa trójkąty prostokątne i oba uzupełnić do dwu prostokątów
2. Twierdzenie Pitagorasa
W dowolnym trójkącie prostokątnym suma kwadratów długości
przyprostokątnych jest równa kwadratowi długości
przeciwprostokątnej tego trójkąta.
Geometrycznie oznacza to, że jeżeli na bokach trójkąta prostokątnego
zbudujemy kwadraty, to suma pól kwadratów zbudowanych na
przyprostokątnych tego trójkąta będzie równa polu kwadratu
zbudowanego na przeciwprostokątnej
a 2 + b2 = c 2
Dowód- układanka na twierdzenie Pitagorasa
Szczepan Jeleński w książce Śladami Pitagorasa przypuszcza, że w ten
sposób mógł udowodnić swoje twierdzenie sam Pitagoras.
Przykłady zadań związanych z twierdzeniem Pitagorasa
1.Czy lustro o wymiarach 2,20m x 2,20m można przenieść przez drzwi o
wymiarach 1m x 1m ?
2. Tam za murem dziewczyna,
a pod ręką drabina,
co pięć metrów długości ma.
W fosie krążą rekiny.
Żal przecudnej dziewczyny,
co za murem z rozpaczy łka.
Czy zwykłemu chłopczynie,
na wspomnianej drabinie,
te przeszkody pokonać się da?
Dane wierszyk pominie.
Znajdziesz je przy rycinie.
Policz sprytnie.
Odpowiedz raz dwa!
3. Odkryli również pięciokąt foremny, wiedzieli o tym, że
płaszczyznę pokrywać można tylko takimi wielokątami
foremnymi: kwadratami, trójkątami równobocznymi oraz
sześciokątami.
4. Klasyfikowali liczby , rozróżniali liczby parzyste
i nieparzyste, doskonałe i niedoskonałe, będące kwadratami
i te nie będące oraz liczby wymierne i niewymierne.
Liczby doskonałe , czyli takie, dla których suma dzielników mniejszych
od liczby równa jest danej liczbie jeżeli tylko liczba jeden jest dzielnikiem
danej liczby. Liczbami doskonałymi są: 6, 28, 496, 8128.
5. Odkryli niewymierności pierwiastek z dwóch.
6. Odkryli prawidłowości dotyczącej znajdywania liczb
całkowitych dla trójkątów pitagorejskich.
Wyraża się ona wzorem:
(2n + 1)² + (2n² + 2n)² = (2n² + 2n + 1)²
7.Pitagorejczycy dokonali też licznych odkryć w innych
dziedzinach m.in. akustyce( że ruch jest przyczyna dźwięku
a także zdefiniowali zjawisko harmonii i wyjaśnili je za
pomocą stosunku liczbowego).
Dalsze zdobycze matematyczne
pitagorejczyków oraz ich zastosowanie
w życiu codziennym
wiadomości o średniej arytmetycznej, geometrycznej i harmonicznej,
zastosowane przez Pitagorasa w muzyce, przejął on również od
matematyków babilońskich.

pitagorejczycy stworzyli szczególne metody badania naukowego.
Matematykę łączyli ściśle z filozofią, ich wiedza była usystematyzowana,
a nowe pojęcia wprowadzali na podstawie logicznego rozumowania,
tworząc elementy podstaw matematyki. Szczególne znaczenie
przypisywali liczbom. Ich mottem było: „wszystko jest liczbą”. Od
pitagorejczyków pochodzi podział na liczby parzyste i nieparzyste. Liczby
przedstawiali w formie figur geometrycznych, układając je z kamyków na
piasku, co pozwoliło im znaleźć sumy prostych ciągów arytmetycznych
(liczby trójkątne i kwadratowe jako sumy szeregów 1 + 2 + ... + n;
1 + 3 + ... + (2n + 1)).


pitagorejczycy odkryli wiele własności liczb i można ich uznać
za twórców początków teorii liczb. Wiedzieli o istnieniu liczb
niewymiernych, ale zobowiązani byli do zachowania tego w tajemnicy.
Istnienie liczb niewymiernych było niezgodne z ich filozofią, niezgodne
z harmonią świata, w którym liczby naturalne odgrywały wg nich
szczególną rolę.

sposób postrzegania świata na podstawie którego budował
swoją filozofię
-mądrość polega na dogłębnej znajomości liczby, poznanie zaś na
rozumieniu harmonii.
-liczba tkwi w rzeczy i dlatego każda rzecz posiada własny model.
Liczba orzeka o istotnej treści rzeczy, stanowi jej formalny wyraz i jest jej
najbardziej formalnym określeniem.
Ciekawostki
•
Odkrycie że długość przekątnej kwadratu o boku długości 1 jest liczba
niewymierną przeraziło pitagorejczyków do tego stopnia, że złożyli przysięgę iż
nikomu nie zdradzą tego faktu. Legenda mówi, że jeden z członków związku
zdradził tajemnicę, a że utonął w morzu, uznano to za karę bogów
•
Legenda głosi, że Pitagoras dostrzegł swoje słynne twierdzenie,
przyglądając się ozdobnym posadzkom.
•
Inne źródła podają, że Pitagoras odkrył to twierdzenie analizując znany już
Egipcjanom trójkąt o bokach 3, 4, 5 (32+42=52). Tak naprawdę niewiadomo jednak,
czy to twierdzenie jest dziełem Pitagorasa, czy też jego uczniów. Jedno jest pewne,
twierdzenie wywarło ogromny wpływ na rozwój nauki w starożytności, a i
współcześnie uznawane jest za jedno z najważniejszych odkryć matematycznych.
•
Pitagorejczycy dzielili liczby na klasy m.in. parzyste, nieparzyste
pierwsze i złożone, doskonałe i zaprzyjaźnione, zajmowali się badaniem
tzw. liczb trójkątnych, kwadratowych, liczby  , którym przypisywali
charakter mistyczny i umieszczając je w centrum filozofii kosmicznej,
według której założeń “wszystko jest liczbą”
• Twierdzenie Pitagorasa znane było Babilończykom i Egipcjanom na długo
przed jego udowodnieniem przez pitagorejczyków.
• Nazwa matematyka bierze początek od grupy uczniów, która wyodrębniła ze
szkoły się po śmierci założyciela.
• Pitagorejczycy ułożyli swoją własną symbolikę liczb :
1 - oznaczała punkt,
2 - linia,
3 - figura geometryczna,
4 - ciało geometryczne (figura w przestrzeni),
5 - własności ciał fizycznych,
6 - życie,
7 - duch,
8 - miłość,
9 - roztropność, sprawiedliwość,
10 - doskonałość wszechświata
•
Pitagoras brał udział w zawodach bokserskich podczas 48. olimpiady w
roku 554 p.n.e. zdobywając tytuł mistrzowski.
• Legenda głosi, że Pitagoras ofiarował bogom 100 wołów jako wyraz
wdzięczności za odkrycie własności trójkątów prostokątnych.
• Pitagorejczycy byli wegetarianami.
• Symbolem szkoły Pitagorasa był pentagram (gwiazda pitagorejska).
Pentagram (gwiazda Pitagorejska)
Pentagram (gwiazda
pięcioramienna) –figura
geometryczna, w wielu kulturach
uważana za symbol magiczny,
gwiazda Salomona. Idealny
pentagram powstaje poprzez
wyrysowanie przekątnych
pięciokąta foremnego i następnie
zamazanie oryginału. Można
również wydłużać boki pięciokąta
do momentu spotkania, otrzymując
większy pentagram.
– Kąt wewnętrzny pentagramu
ma miarę 36°.
– W pentagramie ukryty jest
złoty podział, φ = (1+√5)/2 =
1.61803398….
Pentagram był symbolem bogini Korę, najbardziej wewnętrznej duszy
Matki Ziemi, którą czczono w czasach neolitu. Pentagram był znany
jako Gwiazda Isztar, a później jako Gwiazda Izydy. Mistycy
pitagorejscy widzieli w nim symbol doskonałości, kojarzyli go z życiem
i zdrowiem. W starożytności przekonanie o właściwościach ochronnych
pentagramu było tak silne, że Babilończycy często rysowali go na
pojemnikach z żywnością, co miało zapobiegać jej gniciu. Dla
pierwszych chrześcijan pentagram odzwierciedlał pięć ran Jezusa ze
względu na 5 wierzchołków. Od XIV wieku uważany za symbol
szatana, ze względu na podobieństwo do głowy kozła (odwrócony
dwoma wierzchołkami do góry). W XIX wieku Eliphas Levi podzielił
pentagramy na "dobrą stronę" i "złą stronę". Za "dobrą" uznał ten
odwrócony jednym wierzchołkiem do góry, za "złą" odwrócony —
zwrócony dwoma wierzchołkami do góry. Pentagram zwrócony
jednym wierzchołkiem do góry zwany jest Pentagramem Białym, jest
on odzwierciedleniem sacrum — siły boskiej. Może również
odzwierciedlać pięć zmysłów człowieka, oraz pięć żywiołów:
powietrze, wodę, ziemię, ogień i ducha, ukazując wyższość umysłu
człowieka nad wszelkimi innymi żywiołami i zmysłami.
Trójkąt egipski
Pitagoras przekazał nam
związek między bokami
trójkąta egipskiego:
5
3
3 4 5
2
2
2
4
Pole trójkąta egipskiego wynosi 6, a więc liczbie kolejnej
po trzech liczbach oznaczających długości boków.
Ponadto
6 3 4 5
2
3
2
2
.
Trójkąt o bokach 3, 4 i 5 uważany był w Starożytności
za figurę magiczną. W Egipcie używano go do
wyznaczania kątów prostych przy odnawianiu granic
gruntowych zmywanych dorocznymi wylewami Nilu.
3
5
4
W słynnej piramidzie Cheopsa
tak zwana komnata królewska
ma wymiary w sposób szczególny
związane z liczbami 3, 4, 5.
.
Suma kolejnych liczb nieparzystych daje pełny kwadrat.
1 3  2
2
1 3  5  3
2
1 3  5  7  4
.................
A oto ilustracja geometryczna tego spostrzeżenia.
.
2
Liczba nieparzysta jest różnicą dwu kwadratów.
2 1  3
2
2
3 2  5
2
2
4 3  7
2
2
............
A oto ilustracja geometryczna tego spostrzeżenia.
.
Liczby doskonałe
Liczbami doskonałymi nazywali pitagorejczycy takie
liczby, w których suma podzielników (bez danej liczby)
równa się tej liczbie.
6 = 1 + 2 +3
28 = 1 + 2 + 4 + 7 + 14
496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248
Dzisiaj w dobie komputerów jest znanych ponad 40 liczb
doskonałych (ostatnia ma ponad 19 milionów cyfr)
2
2
32582656
32582657

1
.
Liczby zaprzyjaźnione
Gdy zapytano Pitagorasa: „Co to jest przyjaciel?”
odpowiedział: „Przyjaciel to drugi ja; przyjaźń to
stosunek liczb 220 i 284”.
Dwie liczby są zaprzyjaźnione, jeżeli suma dzielników
każdej z nich (bez niej samej) równa się drugiej liczbie
czyli zaprzyjaźnionej.
220 = 1 +2 + 4 + 71 + 142 , to są dzielniki liczby 284
284 = 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110
Składniki tej sumy są dzielnikami liczby 220
.

Drugim wielkiej doniosłości twierdzeniem
geometrycznym przypisywanym Pitagorasowi
jest twierdzenie o sumie kątów trójkąta
 


      180

.
0
Pitagoras uznawany jest powszechnie za twórcę
pierwszych zasad budowy wielościanów foremnych,
które nazwał figurami kosmicznymi
ikosaedr
oktaedr
dodekaedr
tetraedr
hekasedr
Filozofowie matematycy i ich
osiągnięcia
• Ptolemeusz wybitny astronom grecki podzielił okrąg na 360 równych
części, otrzymując stopień, który podzielił na 60 minut, z kolei minutę na 60
sekund.
• Platon wprowadza pierwszą definicję liczby parzystej- jest to liczba, która
da się podzielić na dwie równe części.
• Apoloniusz z Pergi wprowadził m.in. terminy „parabola”, „hiperbola”,
„elipsa” i „asymptota”. Sądzono, że stożkowe nie są figurami idealnymi,
jakimi powinna się zajmować matematyka. Z punktu widzenia klasyków
Konika nie było dziełem z zakresu matematyki. Niektórzy uważają, że
Apoloniusz z Pergi był jednym z tych, którzy chcieli wyzwolić matematykę
spod wpływów szkoły platońskiej, gdyż starał się znaleźć powiązanie pojęć
matematycznych z otaczającą rzeczywistością. Apoloniusz z Pergi
zajmował się również astronomią; wiele jego odkryć nie zachowało się.
Prace Apoloniusza z Pergi miały ogromny wpływ na rozwój nowożytnej
nauki, w szczególności astronomii, mechaniki i optyki.
Archimedes
Archimedes zajmował się różnymi dziedzinami nauki,
m.in.: arytmetyką, geometrią, hydrostatyką, astronomią,
mechaniką, optyką. Jego prace z matematyki stanowiły
fundament myśli matematycznej kilku stuleci.
Archimedesa uznaje się za jednego z największych
matematyków wszystkich czasów.
-urodził się w Syrakuzach na Sycylii, kształcił się
w Aleksandrii. Podczas drugiej wojny punickiej
kierował obroną Syrakuz, służąc swą wiedzą przy
budowie machin obronnych. Po zdobyciu miasta przez
Rzymian został przypadkowo zabity przez rzymskiego
żołnierza, wbrew rozkazowi zdobywcy Syrakuz –
Marcellusa.
•
-jego dzieła wyróżniały się spośród innych dzieł
starożytności oryginalnością pomysłów, siłą dowodu,
logiczną budową i mistrzostwem rachunku. Do
cenniejszych dzieł matematycznych Archimedesa należą
prace dotyczące rachunku nieskończonościowego.
podjął myśl Eudoksosa, opracowując pomysłowe
metody obliczania pola powierzchni i objętości brył.
•
-ważne dla rozwoju wiedzy matematycznej były
prace, w których Archimedes wprowadził pojęcie
środka ciężkości, określając ten punkt dla najprostszych
figur geometrycznych
• zajmował się też problemami fizyki matematycznej, m.in. problemem dźwigni
i zagadnieniem równowagi ciał zanurzonych
•
zajmował się też problemami fizyki matematycznej, m.in. problemem dźwigni
i zagadnieniem równowagi ciał zanurzonych
•
wprowadzając pojęcie siły, Archimedes stworzył podstawy statyki, określił
zasadę dźwigni
Archimedes, szukając sposobu ustalenia zawartości czystego złota w koronie
króla Hierona II (który panował w czasach Archimedesa), odkrył prawo znane jako
prawo Archimedesa.
jak głosi anegdota, odkrycia tego dokonał podczas kąpieli, po czym,
rozentuzjazmowany wybiegł nago na ulicę Syrakuz z okrzykiem „eureka!”
(znalazłem)
z dziedziny geometrii znane są m.in. takie prace Archimedesa, jak: Pomiar
koła, O liniach spiralnych, O kuli i walcu. Pierwsza z nich zawiera formułę na
obliczenie pola koła oraz dość dokładne oszacowanie liczby p
w traktacie O kuli i walcu Archimedes udowodnił m.in., że objętości brył
geometrycznych o wspólnej osi obrotu – stożka z opisaną na nim kulą, na której
z kolei opisany jest walec – mają się do siebie jak 1 : 2 : 3. Kulę z opisanym na niej
walcem i zaznaczonym stosunkiem objętości tych brył wyryto na życzenie
Archimedesa na jego nagrobku. Cenne są również prace Archimedesa z dziedziny
astronomii i arytmetyki.
opisał mechanizm ruchu Słońca, Księżyca i pięciu planet wokół nieruchomej
Ziemi. Zbudował podobno planetarium z hydraulicznym napędem, które wódz
Rzymian Marcellus zabrał po zdobyciu Syrakuz jako jedyny łup.
•
•
•
•
•
•
w traktacie arytmetycznym O liczbie piasku, obliczając liczbę ziaren
piasku w skończonym, jak to sobie wyobrażali starożytni, wszechświecie
(szacując ją na 1063), Archimedes przedstawił oryginalną metodę
zapisywania bardzo wielkich liczb. Za czasów Archimedesa istniały dwa
systemy liczbowe, w których największą liczbą była liczba 104, zw.
miriadą. Archimedes wprowadził miriady miriad, a największą
wprowadzoną przez niego liczbą była liczba 108 · 1016.
•
uczony zyskał u współczesnych sławę gł. dzięki wynalazkom.
W czasie pobytu w Aleksandrii skonstruował urządzenie znane pod
nazwą śruby Archimedesa, które służyło do nawadniania pól; do dzisiaj
można je spotkać w Egipcie. Skonstruował też przenośnik ślimakowy,
organy wodne i zegar wodny, machiny obronne. Udoskonalił wielokrążek,
który zastosował do wodowania statku. Z tym faktem związane jest
słynne powiedzenie Archimedesa: „Dajcie mi punkt podparcia, a sam
jeden poruszę z posad Ziemię”
•
bryła archimedesowa, wielościan wypukły, którego kąty
wielościenne są przystające, krawędzie są jednakowej długości, a ściany są
wielokątami foremnymi. Różnica między wielościanem półforemnym
a wielościanem foremnym polega na tym, że w wielościanie półforemnym
ściany mogą być różnymi wielokątami foremnymi. Z każdego wielościanu
foremnego (bryły platońskiej) można otrzymać przez odpowiednie
ścinanie naroży pewne wielościany półforemne (bryły archimedesowe).
Wielościany półforemne, które powstają przez ścinanie naroży
wielościanów foremnych.
Bibliografia
• 1.Dirk J. Stiuk “Krótki zarys historii matematyki do końca XIX
wieku”, PWN, Warszawa 1963r.
• 2.Edward Kohler “Z dziejów matematyki”, Wiedza powszechna,
Warszawa 1962r.
• 3. “Encyklopedia szkolna MATEMATYKA”, WSiP SA Warszawa
1998r.
• 4.Jan Legowicz “Zarys historii filozofii”, Wiedza powszechna,
Warszawa 1983r.
Przygotowały:
Katarzyna Andrys, Amanda Kozłowska, Anna Żelichowska
kl. II „a” I L.O. im. T Kościuszki w Busku-Zdroju