TEORIA PRODUKCJI

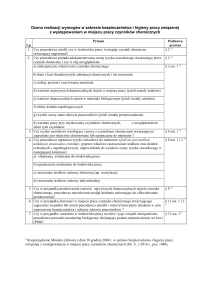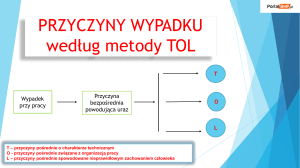
TEORIA PRODUKCJI
Wyznaczanie krzywej możliwości produkcyjnych za pomocą funkcji produkcji
Funkcja produkcji określa maksymalne rozmiary produkcji (Q), jakie można osiągnąć
przy różnym poziomie nakładów czynników wytwórczych, czyli przyjmuje ogólną formułę:
QX = f(L,K,S,Z,γ ,τ ),
gdzie:
QX – wielkość produkcji, L – nakłady pracy, K – nakłady kapitału, S – surowce, półfabrykaty
i materiały, Z – nakład ziemi, γ - korzyści skali, τ - parametr efektywności.
Przy założeniu, że przedsiębiorstwo (gospodarka) używa dwóch czynników wytwórczych –
kapitału (K) i pracy (L) – można ją zapisać w postaci ogólnej jako: Q = f(L,K) w długim
okresie i Q = f(L,
) w krótkim, gdy kapitał jest czynnikiem stałym.
Y
A
TPLY
H
G
II
I
F
E
K
B
C
0
D
J
LY
X
H’
C’
III
IV
B’
LX
TPLX
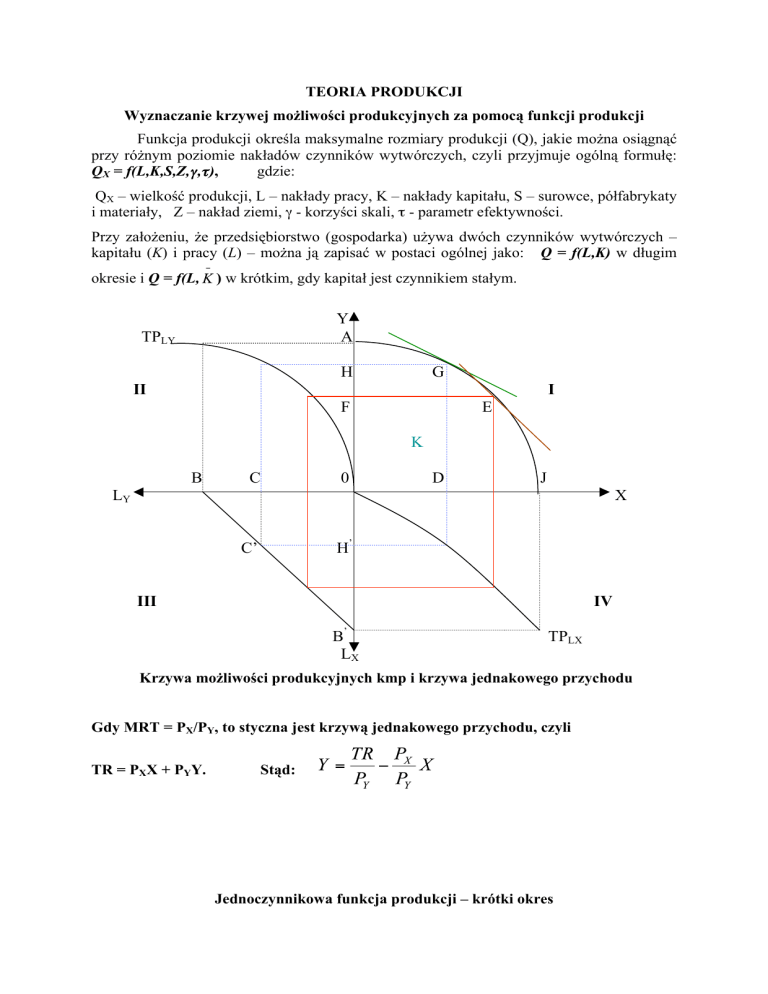
Krzywa możliwości produkcyjnych kmp i krzywa jednakowego przychodu
Gdy MRT = PX/PY, to styczna jest krzywą jednakowego przychodu, czyli
TR = PXX + PYY.
Stąd:
Jednoczynnikowa funkcja produkcji – krótki okres
TPL = X
TPmax
S
R
TPL
0
Lmin
Lmax
Praca
MPL
APL
MPL
0
Lmin
Lmax
APL
Praca
Prawo malejącej produktywności krańcowej – wraz ze wzrostem wykorzystania jednego
czynnika wytwórczego przy pozostałych czynnikach utrzymanych na niezmienionym
poziomie, w strefie produkcji produkt krańcowy czynnika zamiennego maleje.
funkcja odzwierciedla prawo malejącej produktywności krańcowej
dla i = 1, …, k
dla i = 1, … , k
czynnik
Y
130
120
TC1
110
100
90
80
TC2
70
60
50
40
30
Q3
Q2
Q1
20
10
0
0
1
2
3
4
5
6
7
8
9
10
czynnik
11X
W długim okresie wszystkie czynniki wytwórcze są zmienne, a narzędziem analizy są
izokwanty (krzywe jednakowego produktu), czyli zbiór kombinacji różnych nakładów
czynników wytwórczych (metod produkcji), dających jednakowy poziom produkcji.
Nachylenie izokwanty jest krańcową stopą technicznej substytucji (MRTS) jednego
czynnika wytwórczego jednostką czynnika drugiego, gdy zmieniają się metody
wytwarzania, a wielkość produkcji pozostaje bez zmiany. O tym, która kombinacja
zostanie wybrana, decyduje izokoszta (krzywa jednakowego kosztu), nałożona na mapę
izokwant.
Prawa strona równani to nachylenie izokwanty, a lewa to nachylenie
izokoszta. Równość tychże oznacza kombinację najmniejszego kosztu.
Krańcowa efektywność i-tego czynnika (produktywność krańcowa: o ile wzrośnie
produkcja, gdy nakład czynnika wzrośnie o jednostkę, przy pozostałych =
constans)
gdzie:
Δf (x) = f (x1, …, xi + Δxi, …,xk) – f (x1, …, xi,…,xk)
Elastyczność produkcji względem i– tego czynnika określa się:
Eif względem i-tego czynnika pokazuje, o ile procent wzrośnie produkcja, gdy
nakład i-tego czynnika wzrośnie o 1%, a nakłady pozostałe = constans.
Elastyczność produkcji względem skali nakładów (korzyści skali)
Eλ f pokazuje, o ile procent wzrośnie produkcja, jeżeli wszystkie czynniki
produkcji wzrosną o 1%.
Jeżeli funkcja produkcji f : R+k → R+1 jest dodatnio jednorodna stopnia θ >0, to
elastyczność produkcji względem skali nakładów jest równa stopniowi jednorodności tej
funkcji produkcji.
stałe
rosnące
K
malejące
3K
2K
5Q
3K
K
2K
K
0
4Q
3Q
Q
2Q
3Q
Q
L 2L 3L
2K
2Q
K
2Q
Q
0 L2L3L
(a)
0
L 2L
(b)
L
(c)
Korzyści skali dla jednorodnej funkcji produkcji
kapitał
5Q
4Q
3Q
Q
2Q
0
praca
Zmieniające się korzyści skali
K
K
K
Q3
Q2
Q1
0
Q3
Q1 Q2 Q3
L
(a)
Q1
Q2
L
(b)
L
(c)
Szczególne przypadki funkcji produkcji
Zadanie
Przedsiębiorstwo „Asia” do produkcji opon samochodowych wykorzystuje dwa czynniki
zmienne, tj. kapitał i pracę. Funkcja produkcji ma następującą formułę:
TP = 22 L – L2 + 30 K – 3K2
Koszt jednostki pracy w = 5 jp., koszt jednostki kapitału r = 10 jp. Oblicz:
1. ile pracy i kapitału powinno zatrudniać przedsiębiorstwa, aby produkt całkowity
pracy i kapitału był maksymalny?
2. ile wyniesie produkcja przedsiębiorstwa „Asia”, jeżeli zatrudnienie będzie
wynikiem rozwiązania z p. 1?
3. jaki będzie całkowity koszt zatrudnienia kombinacji czynników z p. 1?