Moc w obwodach z pobudzeniem sinusoidalnych w stanie ustalonym

Moc w obwodach z pobudzeniem sinusoidalnych w stanie ustalonym
Sinusoidalnie zmienne źródła prądu elektrycznego są powszechnie stosowane w
energetyce. Wynika to z łatwości generacji w układach elektromaszynowych tego typu
przebiegów, jak również z możliwości przetwarzania parametrów tych przebiegów dla
różnorodnych potrzeb użytkowników, np. zamiany na źródła prądu stałego.
W odróżnieniu od obwodów pobierających prąd stały, moc pobierana ze źródła prądu
sinusoidalnie zmiennego zmienia się w czasie. Dla zbadania charakteru tej zmienności
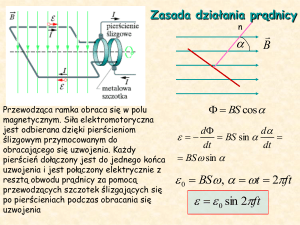
rozpatrzmy dowolny dwójnik (rys. 1) stanowiący pewną gałąź obwodu elektrycznego.
Zapisując zmiany napięcia i prądu w stanie ustalonym w postaci:
u (t ) = U m sin(ωt + ϕ u ), i (t ) = I m sin(ωt + ϕ i )
możemy zapisać wyrażenie na moc chwilową, dostarczoną do tej gałęzi, w postaci:
p (t ) = u (t ) i (t ) = U m sin(ωt + ϕ u ) I m sin(ωt + ϕ i ) .
Im
p(t)
(1)
U
Uo
i(t)
u(t)
ϕu
Ui
I
ϕi
Re
Rys. 1. Strzałkowanie napięcia i prądu oraz mocy dostarczonej do gałęzi. Wykres wskazowy
wartości skutecznych zespolonych napięcia i prądu
Aby zanalizować zależność (1) i zinterpretować wynikające z niej związki zapiszmy
przesunięcie fazowe pomiędzy prądem i napięciem w postaci: ϕ = ϕ u − ϕ i , i na tej podstawie
ϕ u = ϕ i + ϕ . Pozwoli to nam na wydzielenie składowej ui(t) napięcia będącej w fazie z
prądem i składowej do niej ortogonalnej - uo(t):
u (t ) = U m sin(ω t + ϕ + ϕ i ) = U m sin(ω t + ϕ i ) cos(ϕ ) + U m cos(ω t + ϕi ) sin(ϕ ) = ui (t ) + uo (t ),
gdzie ui (t ) = U m sin(ω t + ϕi ) cos(ϕ ) , uo (t ) = U m cos(ω t + ϕ i ) sin(ϕ ) .
Zapiszmy teraz moc chwilową dla składowych zgodnych w fazie (synfazowych):
1
pi (t ) = ui (t ) i (t ) = U m I m sin 2 (ω t + ϕ i ) cos(ϕ ) = U m I m cos(ϕ ) ( 2sin 2 (ω t + ϕi ) )
2
= UI cos(ϕ )(1 − cos(2ω t + 2ϕi )),
( 2sin 2 ( x) = 1 − cos(2 x) )
gdzie U oraz I są wartościami skutecznymi napięcia i prądu gałęziowego. W postaci
uproszczonej:
pi (t ) = P(1 − cos(2ω t + 2ϕ i )) ,
gdzie P = U I cos(ϕ i ) oznacza zarówno wartość średnią tej składowej mocy (tzw. moc
czynna), jak i amplitudę składowej zmiennej tej mocy. Moc tą można nazwać mocą
użyteczną, gdyż jest zamieniana na inne rodzaje energii, bądź na ciepło. Druga ze składowych
mocy, reprezentowana jest przez iloczyn
1
po (t ) = uo (t ) i (t ) = U m I m sin(ϕ ) cos(ω t + ϕ i ) sin(ω t + ϕ i ) = U m I m sin(ϕ ) sin(2ω t + 2ϕi )
2
= U I sin(ϕ ) sin(2ω t + 2ϕi ) = Q sin(2ω t + 2ϕi ),
gdzie Q = U I sin(ϕ ) - amplituda tej składowej, zwana także mocą bierną. Wartość średnia
mocy po(t) jest równa zero. Dlatego p o (t ) reprezentuje tzw. składową bierną (nieużyteczną)
składowej zmiennej mocy.
Ostatecznie, moc chwilowa, dostarczona do gałęzi będzie równa sumie obu
wymienionych składowych:
p(t ) = p i (t ) + p o (t ) = P − P cos(2ω t + 2ϕ i ) + Q sin(2ω t + 2ϕ i ) = P + S sin(2ω t + ϕ i + ϕ u ),
gdzie S = P 2 + Q 2 jest amplitudą składowej zmiennej mocy chwilowej, zwaną także
mocą pozorną.
Z powyższego wynika, że moc w dostarczona do gałęzi obwodu z pobudzeniem
sinusoidalnym zawiera składową stałą zwaną mocą czynną P = U I cos(ϕ ) (za tą moc
płacimy elektrowni), i sinusoidalnie zmienną moc chwilowa oscylującą z amplitudą równą
mocy pozornej S = U I i częstotliwością dwa razy większą niż prąd i napięcie. Amplituda
mocy wnoszonej przez składową ortogonalną jest równa mocy biernej Q = U I sin(ϕ ) .
Składowa ta oscyluje wokół zera i taka też jest jej składowa stała.
Jeżeli przesunięcie fazowe pomiędzy napięciem i prądem mieści się w przedziale
ϕ ≤ π / 2, to mamy wtedy do czynienia z dodatnią mocą czynną ( ( P ≥ 0) pobieraną przez
gałąź, w przeciwnym przypadku moc ta jest ujemna, co oznacza, że gałąź oddaje tą moc na
zewnątrz. Gałęzie złożone z elementów bezstratnych nie pobierają mocy czynnej (wówczas
p(t ) = po (t ) = Q sin(2ω t + 2ϕ i ) ; odpowiada to ϕ = ± π / 2. Gałęzie ze źródłami
autonomicznymi mogą zarówno oddawać moc na zewnątrz ( P < 0) , jak i pobierać moc z
innych gałęzi ( P > 0) , tak jak to ma miejsce w przypadku zamiany prądnicy na silnik.
Moc zespolona
Podane wyżej związki pomiędzy mocą czynną ( Q = U I sin(ϕ ) ), bierną
( P = U I cos(ϕ ) pozorną ( S = U I ) pozwalają na wprowadzenie wielkości integrującej
wszystkie te moce w postaci tzw. mocy zespolonej, „dostarczonej” do dwójnika:
(1)
S = P + jQ = U I cos(ϕ ) + jU I sin(ϕ ) .
Moc ta może być zapisana także z wykorzystaniem zespolonych wartości skutecznych
*
(ZWS) napięcia U i prądu gałęziowego I w postaci: S = U I , gdzie symbol * oznacza
wielkość sprzężoną. Jeśli U oznacza zespoloną wartość skuteczną spadku napięcia, to S
oznacza moc zespoloną dostarczoną do gałęzi. Przy zgodnym strzałkowaniu ZWS napięcia i
prądu gałęziowego jest to zespolona moc oddawana na zewnątrz, do innych gałęzi obwodu.
Moc zespolona może być wykorzystana do zapisu bilansu mocy gałęziowych
obwodów spełniających postulaty zapisane w postaci zespolonych praw Kirchhoffa dla
pobudzeń sinusoidalnych o tej samej pulsacji. Jeżeli U i I reprezentują wektory kolumnowe
utworzone z ZWS napięć i prądów gałęziowych obwodu elektrycznego, wówczas suma
wszystkich zespolonych mocy jest równa S = UT I *, gdzie T oznacza transpozycję wektora
(zamianę wektora kolumnowego na wierszowy). Ponieważ taka sieć nie pobiera, ani nie
oddaje energii do otoczenia, a zatem S = UT I *= 0. Równość ta oznacza także, że suma mocy
czynnych i suma mocy biernych wszystkich gałęzi obwodu elektrycznego jest równa zero.
Można to równość, zwaną bilansem mocy, wykorzystać do sprawdzenia poprawności
rozwiązania obwodów. Wyznaczone napięcia i prądy gałęziowe muszą spełniać warunki
bilansu mocy zespolonych, mocy czynnych i biernych, zapisane w sposób niejawny w
prawach Kirchhoffa.
Dla odróżnienia poszczególnych składowych mocy przyjęto, jako jednostkę mocy
czynnej P 1W (wat), mocy biernej 1Var (var), mocy pozornej 1VA (voltamper).