Zestaw zadań maturalnych z matematyki `2010 Opracowały: Monika

Zestaw zadań
maturalnych
z matematyki
‘2010
Opracowały: Monika Chłopik i Magdalena
Chudzyńska
Liczby, ich zbiory
1. Po wykonaniu działań na potęgach
A. a 11
B. a 6
(a 2 ) 3
otrzymamy:
a 5
C. a
D. a 1
2. Wiadomo, że 8% pewnej liczby jest równe 10. Zatem 10% tej liczby wynosi:
A.12,5
B. 15
C. 18
D. 8
3. Liczba 0,5log0,01 jest równa:
A. 0,005
B. 0,5
C. -0,5
D. -1
4. Liczba 8 log 3 jest równa:
2
A. 2
B.24
C. 9
D.27
1 3
  27
3
 9 jest równa:
5. Wartość wyrażenia
32
1
1
A. 1
B. -1
C.
D. 
3
3
6. Liczba x jest o 30% większa od liczby y. Z tego wynika, że:
A. y=0,7x
B. x=1,3y
C. y=1,3x
D. x=0,3y
7. Liczba 5 5 jest równa:
A. 5
B. 2  5 0,5
C. 5 0, 75
D.
5
8. Przybliżenie z nadmiarem liczby dodatniej x wynosi 13. Błąd względny tego przybliżenia wynosi
0,04. Wobec tego:
A. x = 13,52
B. x = 13,5
C. x = 12,5
D. x = 12,48
9. Liczba (7  2 3 ) 3 jest równa:
A. 37
C. 61-14 3
B. 61

2
3
10. Wśród liczb należących do zbioru M= 0, (73); 36 ; ; 24 ;
A. 1
B. 2

C. 3
D. 61-28 3
5 25 
;
 liczb wymiernych jest:
4
2 
D. 4
Zadania otwarte krótkiej odpowiedzi:
1. Na wycieczkę pojechało 7 dziewczyn, które stanowiły 43,75% liczby wszystkich uczestników
wycieczki. Ile osób pojechało na wycieczkę?
2. Liczbę (1  3 ) 3 zapisz w postaci a b  c , gdzie a, b, c są liczbami całkowitymi.
2
3. Dane są przedziały A= (-4, 3), B=  1,8 . Wyznacz przedziały A  B oraz B \ A.
1
4. Oblicz liczbę x 3 , jeżeli wiadomo, że x=
1
(64) 3  16 4
.
8
5. Dane jest wyrażenie W= 4x  10  x  5 . Zapisz wartość tego wyrażenia bez symbolu wartości
bezwzględnej dla dowolnej liczby x  (2,5) .
3
6. Rozwiąż równanie ( x  3) 2  6.
7. Zapisz liczbę 365400000 w postaci a  10 k , gdzie k  1,10) i k  C .
Zadania otwarte rozszerzonej odpowiedzi:
1. Sznurek o długości 2,8 m przecięto na trzy części, których długości są w stosunku 3:5:6. Oblicz
długość każdej części. Sprawdź, czy najdłuższa część wystarczy do obwiązania pudełka w kształcie
prostopadłościanu o wymiarach 25cm, 18cm, 30 cm, jeśli mamy je przewiązać jednokrotnie wzdłuż
ścian o najdłuższych wymiarach.
2. Wymień wszystkie liczby pierwsze, które spełniają jednocześnie nierówność
1
x7  4 i
2
nierówność x 2  12 x  0 .
3. Liczbę odwrotną do liczby 3 
4
5
zapisano w postaci a 3  b 5 . Znajdź liczby a i b.
Funkcje i ich własności
2
3
1. Wykresem funkcji y  x  5 jest prosta prostopadła do wykresu funkcji:
A. y 
2
1
x
3
5
2
B. y   x  5
3
C. y
3
x5
2
3
1
D. y   x 
2
5
2. Osią symetrii funkcji kwadratowej f ( x)  4 x 2  8x  8 jest prosta o równaniu:
A. y  8  0
B. x  1  0
C. x  2
D. y  1
3 3 8
) jest:
2
D. niewymierna
3. Funkcja liniowa f opisana jest wzorem: f ( x)  2 x  3 3 . Zatem liczba f (
A. złożona
B. pierwsza
C. ujemna
4. Miejscem zerowym funkcji liniowej f ( x)  (a  1) x  3 jest liczba -3. Liczba a jest równa:
A. -1
B. 0
C. 2
D. 1
5. Wykres funkcji g ( x)  (2 x  1)( x  2) przecina oś OY w punkcie:
A. (0,0)
B. (2,0)
C. (0,2)
D. (0,-2)
6. Dziedziną funkcji f ( x)  6  2 x jest przedział:
3
A. 0,)
B. (, 0
7. Funkcja g ( x) 
x
dla argumentu x  2 przyjmuje wartość:
x2
B. 2  1
C. 2  1
D. 2  2
A.
2
C. (, 3
D. (, 6
8. Funkcja f ( x)  6 x  2 wartość 2 przyjmuje dla argumentu:
A. -14
B. 
2
3
C. 0
D.
1
6
9. Liczba miejsc zerowych funkcji h( x)  x 3  25x jest równa:
A. 0
B. 1
C. 2
D. 3
10. Do wykresu funkcji f ( x)  x  3 należy punkt:
A. (2,-1)
B. (5,2)
C. (3,0)
D. (9,3)
Zadania otwarte krótkiej odpowiedzi:
1. Wyznacz dziedzinę funkcji f ( x)  x 2  6 x  9 .
2. Liczba -3 jest jednym z miejsc zerowych funkcji g ( x)  x 2  4 x  c. Oblicz wartość funkcji g dla
argumentu -1.
3x  2, gdy x  0
 x  3, gdy x  0.
3. Naszkicuj wykres funkcji f określonej wzorem f ( x)  
4. Napisz wzór funkcji liniowej, której wykres jest prostopadły do wykresu funkcji o wzorze
f ( x)  2 x  1 i przechodzi przez punkt (-2,3).
5. Funkcja określona wzorem g ( x)   x 2  bx  25 osiąga największą wartość dla argumentu 5.
Wyznacz współczynnik b.
6. Funkcja f przyporządkowuje każdej liczbie naturalnej resztę z dzielenia tej liczby przez 5.
a) Podaj zbiór wartości funkcji f .
b) Naszkicuj wykres funkcji f dla x  2,3,4,5,6,7.
x  1
7. Wyznacz miejsce zerowe funkcji h( x)  
dla x  2
2
 x  4 dla x  2
.
Zadania otwarte rozszerzonej odpowiedzi:
1. Funkcja f określona jest wzorem f ( x)  5  x  x  5  x .
a) Wyznacz dziedzinę funkcji f .
b) Sprawdź, czy liczby f (1), f 4 są wymierne.
c) Uzasadnij, że f (3)  3 ( 6  1).
2. Miejscem zerowym funkcji f ( x)  2 x  b jest liczba 1,5.
a) Oblicz współczynnik b.
4
b) Dla jakich argumentów wartości funkcji f są większe od wartości funkcji g ( x)  3x  7.
c) Znajdź te argumenty, dla których funkcja f i funkcja h( x)  x 3  x 2  5x przyjmują tę samą wartość.
3. Suma kwadratów dwóch kolejnych liczb naturalnych jest o 133 większa od iloczynu tych liczb.
Znajdź te liczby.
Wielomiany i funkcje wymierne
1. Liczba rozwiązań równania
A. 0
B. 1
3x 2  12
 0 jest równa:
x 2  4x  4
C. 2
D. 3
2. Liczba pierwiastków wielomianu W(x)= x( x  1)( x 2  9) jest równa:
A. 1
B. 2
C. 3
D. 4
3. Jeżeli wielomiany P( x)  x 4  5x 2  3 i Q( x)  ( x 2  5)( x 2  10)  c są równe, to:
A. c=3
B. c=8
C. c=47
D. c=53
1
5
4.:Pierwiastkiem wielomianu W ( x)   x  x 2  36 jest liczba:
3
A. -6
B.
5
6
6
C. 2,5
D. 10
5.Wartość wielomianu W ( x)  2 x 3  2 x 2 dla x  2 jest równa:
A. -24
B. -8
6. Rozwiązaniem równania
A.-2
B.0
C. 8
D. 24
x4
 0 jest liczba:
x2
C.2
D. 4
7. Jeżeli punkt A=(2, q) należy do wykresu funkcji f ( x) 
A.-6
B.-1
C.1
D. 5
8. Jeżeli dla pewnej ujemnej liczby u zachodzi równość
A. -24
B. -12
6
, to suma jego współrzędnych jest równa:
x
C. -8
x2 1
9. Rozwiązaniem równania
 1 jest liczba:
x 1
A. -1
B. 0
C. 2
u 9
72
 , to wyrażenie
ma wartość:
4 u
u
D. -2
D. 1
m2  k 2
10. Jeżeli dla pewnych liczb k i m zachodzi równość
 16 , to suma liczb k i m jest równa:
mk
A. 4
B. 8
C. 16
D. 32
5
Zadania otwarte krótkiej odpowiedzi:
1. Wyznacz miejsca zerowe funkcji w( x)  x 5  9 x 3  8x 2  72.
2. Rozwiąż równanie
2
 1  x. .
x 1
3. Prosta o równaniu y=-6 przecina hiperbolę o równaniu y 
15
w punkcie P. Podaj współrzędne
x
punktu P.
4. Zapisz wielomian P( x)  x 3 ( x 3  2 x  1)  x 2 ( x 4  2 x  1) w prostszej postaci i określ jego stopień.
5. Rozwiąż równanie 16 x 4  9  0.
6. Jednym z pierwiastków wielomianu W ( x)  3x 3  bx jest 3. Znajdź pozostałe pierwiastki tego
wielomianu.
7. Wyznacz dziedzinę wyrażenia
x
x  x  11x  11.
3
2
Zadania otwarte rozszerzonej odpowiedzi:
1. Wiedząc, że
5 y  2x
5x  2 y
 4 , oblicz wartość wyrażenia
5 y  2 x.
5x  2 y
2. Wartość wielomianu Q( x)  x 3  bx 2  9 x  d dla x=1 wynosi 8, a jednym z jego pierwiastków jest
3. Rozłóż wielomian Q (x) na czynniki liniowe.
2
2 x
.
x
x2
a) Naszkicuj wykresy obu funkcji w jednym układzie współrzędnych.
b) Określ przedziały monotoniczności obu funkcji.
c) Podaj zbiór rozwiązań nierówności f ( x)  g ( x).
3. Dane są funkcje f ( x)   1 i g x  
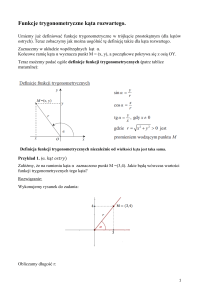
Funkcje trygonometryczne
2
5
1. Kąt  jest ostry i sin   . Wówczas cos  jest równy:
A.
3
5
B.
5
2
C.
21
5
D.
3
5
2. Przekątna rombu tworzy z jego bokiem kąt 30 0 . Wiadomo, że bok rombu ma długość 6 cm. Dłuższa
przekątna rombu ma długość:
A. 3 3
B. 3
C. 6
D. 6 3
6
3. Dany jest trójkąt równoramienny o wysokości 24, podstawie 20 i ramieniu 26. Kąt  jest kątem przy
podstawie trójkąta. Wynika stąd, że:
5
5
A. sin  
B. cos  
13
12
C. tg 
12
13
D. sin  
12
13
4. Wyrażenie sin   cos 2   sin 3  , gdzie  jest kątem ostrym, jest równe:
A. cos 
C. sin 
B. 1
D. tg
5. Liczba 2 cos 30 0 równa jest liczbie:
A. cos 60 0
B. sin 60 0
C. tg 60 0
D. tg30 0
6. Liczba (sin 450  cos 450 ) 2 równa jest:
A.1
B.
C.2
2
D. 2 2
7. Liczba log 3 tg 60 0 jest równa:
A.-1,5
B.-1
C.-0,5
D. 0,5
3
5
8. Jeżeli tangens kąta  jest równy , to iloraz
A.
3
5
B.
3
4
C.
5
4
cos 
jest równy:
sin 
5
D.
3
9. Liczba 5sin 15  5cos 15 jest równa:
2
0
2
A. 15
0
B. 1
C. 5
D. 25
10. Suma sinusów kątów ostrych trójkąta prostokątnego, którego przyprostokątne mają długość 1i 3,
jest równa:
2
A.
5
B.
2 5
5
C.
10
5
D.
2 10
5
Zadania otwarte krótkiej odpowiedzi:
1. Tangens kąta ostrego  jest równy
5
. Oblicz sinus kąta  .
3
2. Sprawdź, czy liczba log 2 sin 60 0  log 2 tg30 0 jest całkowita..
3. Boki trójkąta mają długości 3 cm, 4 cm, 5 cm. Znajdź miarę kąta między bokami o długościach 4 cm i
5 cm.
4. Wyznacz kąt ostry  , wiedząc, że log 2 sin   1.
5. W trójkącie prostokątnym przeciwprostokątna ma długość 12, a jeden z kątów ostrych 30 0 . Wyznacz
długości pozostałych boków trójkąta.
6. Sprawdź, czy liczba
1
1
 (sin 60 0  cos 60 0 )   (tg30 0  tg 60 0 ) jest wymierna.
3
8
7..Jaki kąt ostry tworzy prosta o równaniu y  3tg30 0 x z prostą o równaniu y  0 ?
7
Zadania otwarte rozszerzonej odpowiedzi:
1. Wyznacz miarę kąta ostrego  wiedząc, że liczba sin  jest rozwiązaniem równania
2 x 2  7 x  3  0.
2. Wiedząc, że sinus kąta ostrego  jest równy
8  15
, oblicz wartość liczbową wyrażenia
4
(sin   cos  ) 2 .
3. Wiedząc, że 4 sin 2   3 cos 2   3 i  jest kątem ostrym, oblicz tg.
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Literatura:
1.”Obowiązkowa matura z matematyki- testy”, Marzena Orlińska, wyd. Operon.
2.”Zestawy maturalne- poziom podstawowy”, W. Babiański, L. Chańko, wyd. Nowa Era
3.”Matura z matematyki od roku 2010”, A.Cewe, H.Naharska, wyd. Podkowa
4.”Matura z matematyki”, A.Kiełbasa, wyd. 2000
28