zbiór liczb naturalnych Z

Wykład 1
Oznaczenia zbiorów
N - zbiór liczb naturalnych
Z - zbiór liczb całkowitych
Q - zbiór liczb wymiernych
R - zbiór liczb rzeczywistych
Definicja 1 Iloczynem kartezjańskim zbiorów X i Y (ozn. X × Y ) nazywamy zbiór:
(
∅,
gdy X = ∅ lub Y = ∅
X × Y :=
.
{(x, y) : x ∈ X, y ∈ Y }, gdy X =
6 ∅ i Y 6= ∅
Definicja 2 Działaniem dwuargumentowym w zbiorze X (krótko: działaniem) nazywamy każdą
funkcję ◦ : X × X → X.
Oznaczenie: x ◦ y := ◦(x, y)
Definicja 3 Działanie ◦ w zbiorze X jest
łączne, jeśli ∀x, y, z ∈ X (x ◦ y) ◦ z = x ◦ (y ◦ z)
przemienne, jeśli ∀x, y ∈ X x ◦ y = y ◦ x.
Definicja 4 Element e ∈ X jest elementem neutralnym działania ◦, jeśli
∀x ∈ X x ◦ e = e ◦ x = x.
Definicja 5 Niech e będzie elementem neutralnym działania ◦ w zbiorze X. Element y ∈ X jest
elementem odwrotnym do elementu x ∈ X (w sensie działania ◦), jeśli
x ◦ y = y ◦ x = e.
Definicja 6 Parę (G, ◦) nazywamy grupą, jeśli ◦ jest działaniem w zbiorze G oraz
1. działanie ◦ jest łączne,
2. istnieje element neutralny działania ◦,
3. dla każdego x ∈ G istnieje element odwrotny.
Uwaga. Jeśli działanie ◦ jest przemienne, to grupę (G, ◦) nazywamy grupą przemienną.
Liczby zespolone
Niech C := {(x, y) : x, y ∈ R}. Definiujemy w tym zbiorze następujące działania:
mnożenie przez liczby rzeczywiste:
α · (x, y) := (αx, αy) := (x, y) · α, α ∈ R
dodawanie:
(x1 , y1 ) ⊕ (x2 , y2 ) := (x1 + x2 , y1 + y2 )
mnożenie:
(x1 , y1 ) (x2 , y2 ) := (x1 x2 − y1 y2 , x1 y2 + x2 y1 )
Działania ⊕ i są przemienne i łączne.
Liczba (0, 0) jest elementem neutralnym działania ⊕.
Liczba (1, 0) jest elementem neutralnym działania .
(x, y) = x(1, 0) + (0, 1)y
(0, 1)2 = −(1, 0)
Oznaczenia. (1, 0) = 1, (0, 1) = j, gdzie j 2 = −1,
j nazywamy jednostką urojoną
1
Postać kanoniczna liczby zespolonej
z =x+j·y
x - część rzeczywista liczby zespolonej z, ozn. x =Re z
y - część urojona liczby zespolonej z, ozn. y =Im z
Uwaga. Liczby zespolone z1 i z2 są równe wtedy i tylko wtedy, gdy (Re z1 =Re z2 i Im z1 =Im z2 ).
Uwaga. Niech z1 = x1 + jy1 , z2 = x2 + jy2 . Wtedy
z1 + z2 = (x1 + x2 ) + j(y1 + y2 )
z1 · z2 = (x1 x2 − y1 y2 ) + j(x1 y2 + x2 y1 )
Definicja 7 Liczbą sprzężoną z liczbą zespoloną z = x + jy nazywamy liczbę z = x − jy.
Uwaga.
z1 + z2 = z1 + z2
z1 · z2 = z1 · z2
Dzielenie liczb zespolonych:
z1
z1 · z2
=
, dla z2 6= 0
z2
z2 · z2
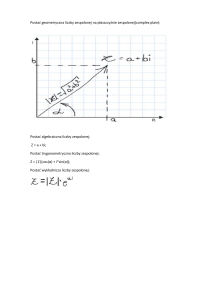
Interpretacja geometryczna liczby zespolonej
Imz
6
r (x, y) ↔ x + jy
y
x
Definicja 8 Liczbę rzeczywistą
przez |z|.
Rez
p
x2 + y 2 nazywamy modułem liczby zespolonej z = x+jy i oznaczamy
Uwaga. Na płaszczyźnie zespolonej:
|z| - odległość punktu z od początku układu O
|z1 − z2 | - odległość punktów z1 i z2
Własności modułu
1. |z| = 0 ⇔ z = 0
2. |z1 + z2 | ¬ |z1 | + |z2 | (nierówność trójkąta)
3. |z1 · z2 | = |z1 | · |z2 |
4. |
z1
|z1 |
|=
, dla z2 6= 0
z2
|z2 |
5. |z|2 = z · z
6. |z| = |z|
Postać trygonometryczna liczby zespolonej
Imz
y
6
©rz = x + jy
|z|©©
©
φ
©©
x Rez
2
Twierdzenie 1 Dla każdej liczby zespolonej z = x + jy, z 6= 0, istnieje dokładnie jedna liczba φ ∈
y
x
(−π; πi, taka że cos φ = |z|
i sin φ = |z|
.
Liczbę φ nazywamy argumentem głównym liczby zespolonej z, ozn. φ = arg z.
Każdą liczbę zespoloną z 6= 0 można przedstawić w postaci trygonometrycznej:
z = |z|(cos β + j sin β), gdzie β ∈ R.
Jeśli φ = arg z, to β = φ + 2kπ, gdzie k ∈ Z.
Liczbę β nazywamy argumentem liczby z, ozn. β = Argz.
Uwaga. Liczba z = 0 nie posiada argumentu.
Uwaga. arg z = − arg z.
Uwaga. Jeśli z1 = |z1 | · (cos φ1 + j sin φ1 ), z2 = |z2 | · (cos φ2 + j sin φ2 ), to:
z1 · z2 = |z1 | · |z2 | · (cos(φ1 + φ2 ) + j sin(φ1 + φ2 ))
z1
|z1 |
=
· (cos(φ1 − φ2 ) + j sin(φ1 − φ2 )).
z2
|z2 |
Wzór Moivre’a: z n = |z|n · (cos nφ + j sin nφ)
W szczególności: (cosφ + j sin φ)n = cos nφ + j sin nφ.
Wzory Eulera:
ex+jy := ex · ejy
ejy := cos y + j sin y
Postać wykładnicza liczby zespolonej
z = |z| · ejφ .
3