Liczby zespolone

Liczby zespolone
1
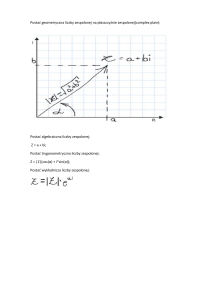
Definicja: C = R × R = {(a, b); a, b ∈ R}.
Działania w C:
(a, b) + (c, d) = (a + c, b + d),
(a, b) · (c, d) = (ac − bd, ad + bc).
Para (a, 0) odpowiada liczbie rzeczywistej a:
(a, 0) + (c, 0) = (a + c, 0), (a, 0) · (c, 0) = (ac, 0).
Przyjmując i = (0, 1) mamy:
a + bi = (a, 0) + (b, 0) · (0, 1) = (a, 0) + (0, b) = (a, b),
i2 = (0, 1) · (0, 1) = (−1, 0) = −1.
2
Liczbę zespoloną z można jednoznacznie przedstawić w postaci
z = a + bi,
gdzie a, b ∈ R.
Na płaszczyźnie Gaussa liczbie z odpowiada punkt o współrzędnych (a, b).
Działania wykonujemy jak na wyrażeniach algebraicznych, pamiętając o tym, że
i2 = −1.
Dodawanie: (a + bi) + (c + di) = (a + c) + (b + d)i.
Mnożenie:
(a + bi) · (c + di) = ac + adi + bci + bdi2 = (ac − bd) + (ad + bc)i.
3
Własności działań na liczbach zespolonych
1. ∀z1,z2,z3∈C (z1 + z2) + z3 = z1 + (z2 + z3)
2. ∀z1,z2∈C z1 + z2 = z2 + z1
3. ∃0∈C∀z∈C z + 0 = z, zero: 0 = 0 + 0 · i
4. ∀z∈C∃w∈C z + w = 0, oznaczenie: w = −z,
z = a + bi ⇒ −z = (−a) + (−b)i
4
5. ∀z1,z2,z3∈C (z1 · z2) · z3 = z1 · (z2 · z3)
6. ∀z1,z2∈C z1 · z2 = z2 · z1
7. ∃1∈C∀z∈C z · 1 = z, jedynka: 1 = 1 + 0 · i
8. ∀z∈C\{0}∃w∈C z · w = 1, oznaczenie: w = z −1,
−b
a
+
·i
z = a + bi ⇒ z −1 = 2
2
2
2
a +b
a +b
9. ∀z1,z2,z3∈C (z1 + z2) · z3 = z1 · z3 + z2 · z3
5
Odejmowanie i dzielenie liczb zespolonych
Odejmowanie: z1 − z2 = z1 + (−z2),
(a + bi) − (c + di) = (a − c) + (b − d)i.
z1
Dzielenie:
= z1 · z2−1,
z2
a + bi
(a + bi)(c − di)
(a + bi)(c − di)
=
=
.
2
2
c + di
(c + di)(c − di)
c +d
Mamy:
1
= z −1.
z
1 + 2i
(1 + 2i)(2 + 3i)
2 + 3i + 4i + 6i2
=
=
=
Przykład:
2
2
2 − 3i
(2 − 3i)(2 + 3i)
2 +3
−4 + 7i
4
7
=
=−
+
· i.
13
13
13
6
Potęgowanie liczb zespolonych
Dla liczby zespolonej z i liczby naturalnej n > 0 przyjmujemy:
z n = |z · z ·{z. . . · z} .
n
Ponadto, jeśli z 6= 0, to przyjmujemy z 0 = 1 oraz
z −n = (z −1)n = |z −1 · z −1{z· . . . · z −1} .
n
Zauważmy, że (z −1)n = (z n)−1.
Dla liczb całkowitych m, n zachodzą wzory:
m
z
z m+n = z mz n, z m−n = n , z mn = (z m)n.
z
7
Postać algebraiczna liczby zespolonej: z = a + bi, a, b ∈ R,
część rzeczywista: Re z = a,
część urojona: Im z = b,
liczba sprzężona: z = a − bi.
√
Przykład. Dla z = 2 − 3i mamy:
√
√
Re z = 2, Im z = − 3, z = 2 + 3i.
8
Własności sprzężenia liczby zespolonej
1. z1 + z2 = z1 + z2
2. z1 − z2 = z1 − z2
3. z1 · z2 = z1 · z2
4.
z1
z2
!
=
z1
z2
5. (z) = z
6. z = z ⇔ z ∈ R
9
Moduł i argument liczby zespolonej
Definicja. Modułem liczby zespolonej z = a + bi (gdzie a, b ∈ R)
nazywamy liczbę rzeczywistą
|z| =
Przykład: |3 + 4i| =
q
q
a2 + b2.
32 + 4 2 =
√
25 = 5.
Na płaszczyźnie Gaussa moduł liczby z jest równy jej odległości
od liczby 0. Odległość liczb z1 i z2 jest równa |z1 − z2|.
10
Własności modułu:
1. | − z| = |z|, |z| = |z|
2. z · z = (a + bi)(a − bi) = a2 + b2 = |z|2
3. |z1 · z2| = |z1| · |z2|
z |z |
4. 1 = 1
z2
|z2|
5. |z1 + z2| 6 |z1| + |z2|
11
Definicja. Argumentem liczby zespolonej z = a + bi 6= 0 (gdzie
a, b ∈ R) nazywamy liczbę rzeczywistą ϕ spełniającą warunki

a


,
cos
ϕ
=

r
b


 sin ϕ = ,
r
gdzie r = |z| =
q
a2 + b2.
Argument liczby zespolonej jest określony z dokładnością do wielokrotności 2π, tzn. jeśli ϕ jest argumentem liczby z, to ϕ + 2kπ
(dla k ∈ Z) też jest argumentem liczby z.
Jako argument liczby 0 możemy przyjąć dowolną liczbę rzeczywistą ϕ.
12
Na płaszczyźnie Gaussa argument liczby z to miara kąta zorientowanego, jaki tworzy dodatnia półoś rzeczywista z półprostą o
początku 0, przechodzącą przez z.
Liczba z ma jednoznacznie określony argument z przedziału [0, 2π).
Argument ten nazywamy argumentem głównym.
Oznaczenie argumentu (głównego): ϕ = arg z.
Uwaga. Czasami wygodniej jest wybrać argument z przedziału
(−π, π].
13
Postać trygonometryczna liczby zespolonej
Dla r = |z| mamy a = r cos ϕ, b = r sin ϕ, więc
z = r(cos ϕ + i sin ϕ),
gdzie r, ϕ ∈ R, r > 0.
Mnożenie i dzielenie liczb zespolonych w postaci trygonometrycznej:
r(cos ϕ + i sin ϕ) · s(cos ψ + i sin ψ) = rs(cos(ϕ + ψ) + i sin(ϕ + ψ))
r
r(cos ϕ + i sin ϕ)
= (cos(ϕ − ψ) + i sin(ϕ − ψ))
s(cos ψ + i sin ψ)
s
14
Wzór de Moivre’a
(cos ϕ + i sin ϕ)n = (cos nϕ + i sin nϕ)
Przykład:
(1 + i)100 =
√
π
π 100
=
2(cos + i sin )
4
4
= 250(cos 25π + i sin 25π) = −250.
15
Pierwiastek liczby zespolonej
Pierwiastkiem stopnia n liczby z ∈ C nazywamy liczbę w ∈ C taką,
że wn = z.
Przykłady.
1) Liczba i jest pierwiastkiem kwadratowym (tzn. stopnia 2)
liczby −1, liczba −i też!
2) Liczby 2, −2, 2i i −2i są pierwiastkami stopnia 4 liczby 16.
3) Liczba 1 + i jest pierwiastkiem stopnia 100 liczby −250.
16
Liczba zespolona z 6= 0 ma dokładnie n pierwiastków stopnia n.
Jeśli
z = r(cos ϕ + i sin ϕ),
gdzie r, ϕ ∈ R, r > 0, to wszystkie pierwiastki stopnia n liczby z
są postaci
√
ϕ + 2kπ
ϕ + 2kπ n
wk = r cos
+ i sin
,
n
n
gdzie k = 0, 1, . . . , n − 1.
Na płaszczyźnie Gaussa pierwiastki stopnia n danej liczby zespolonej są wierzchołkami n-kąta foremnego o środku 0.
17
Przykład. Pierwiastkami stopnia 4 liczby
√
√
2π
2π
− 3 + 3i = 2 3(cos
+ i sin
)
3
3
są liczby
2π + 2kπ 2π + 2kπ
+ i sin 3
3 cos 3
=
q √ 4
2
4
4
√
√
π
kπ
π
kπ 8
4
) + i sin( +
)
= 2 3 cos( +
6
2
6
2
dla k = 0, 1, 2, 3.
18
Zasadnicze twierdzenie algebry. Wielomian stopnia n > 0 o
współczynnikach zespolonych posiada (z uwzględnieniem krotności) dokładnie n pierwiastków.
Zatem dla dowolnego wielomianu o współczynnikach zespolonych
W (T ) = anz n + an−1z n−1 + . . . + a1z + a0
istnieją liczby zespolone z1, z2, . . . , zn (niekoniecznie różne) takie,
że
W (T ) = an(z − z1)(z − z2) . . . (z − zn).
Wniosek. Wielomian stopnia n > 0 o współczynnikach rzeczywistych można rozłożyć na czynniki stopnia 1 i 2.
19