Lczby_zespolone (1) - Matematyka - martinoo88k

Lczby_zespolone (1).doc
(1850 KB) Pobierz
Tomasz Grębski
Liczby zespolone
Kraśnik 2001
Spis Treści:
Wstęp ……………………………………………………………………….
3
Podstawowe wiadomości o liczbie zespolonej ……………………………..
4
Interpretacja geometryczna liczby zespolonej ……………………………...
4
Moduł liczby zespolonej. Liczby sprzężone. ……………………………….
5
Postać trygonometryczna liczby zespolonej ………………………………..
7
Wzór de Moivre’a …………………………………………………………..
9
Pierwiastek stopnia n z liczby zespolonej ………………………………….
10
Rozwiązywanie równań kwadratowych w zbiorze liczb zespolonych ……..
12
Pierwiastek pierwotny n-tego stopnia z jedności …………………………...
13
Zadania ……………………………………………………………………... 14
Odpowiedzi do zadań ………………………………………………………. 18
Bibliografia ………………………………………………………...……….
23
Wstęp
Jestem nauczycielem matematyki i informatyki w Zespole Szkół Nr 2 im. Mikołaja Reja w
Kraśniku. Pragnę przedstawić Państwu referat dotyczący liczb zespolonych. Zamierzeniem moim było
zebranie najważniejszych wiadomości o tych liczbach, omówienie ich własności oraz przedstawienie
przykładowych zadań z ich zastosowaniem. Jako uzupełnienie podałem kilkadziesiąt zadań wraz z
odpowiedziami.
Omówione w referacie zagadnienia osobiście stosuję podczas kółka matematycznego oraz jako
dodatkowe lekcje w klasach o profilu matematyczno – fizycznym i informatycznym. Cieszą się one
dużym zainteresowaniem, rozwijają wyobraźnię uczniów i są pomocne w przygotowaniu się do
egzaminu na wyższe uczelnie.
Mam nadzieję, że i Państwo wykorzystają ten referat w swojej pracy jak również Państwa uczniowie.
Referat dostępny jest również w formie elektronicznej na mojej stronie internetowej pod adresem:
www.matma.krasnik.com.pl.
Tomasz Grębski
Podstawowe wiadomości o liczbie zespolonej
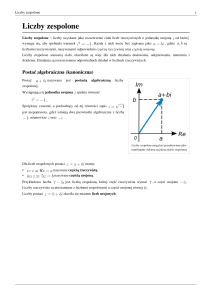
Liczbą zespoloną nazywamy wyrażenie a + bi, gdzie a i b są liczbami rzeczywistymi , i2 = -1
Dla dowolnych liczb zespolonych (a + bi), i (c + di) mamy:
1. (a + bi) = (c + di)  a = c i b = d .
2. (a + bi) + (c + di) = (a + c) + (b + d)i,
3. (a + bi) – (c + di) = (a – c) + (b – d)i,
4. (a + bi)·(c + di) = ac + adi + bci + bdi2 = (ac - bd) + (ad + bc)i,
gdyż i2 = -1
5. (a + bi) : (c + di) =
Wzór 5 otrzymamy mnożąc dzielną i dzielnik przez c – di
=
=
+
+
i
przyjmując i2= -1
W zbiorze liczb zespolonych nie można określić nierówności.
Pojęcie potęgi o wykładniku naturalnym, zerowym i ujemnym liczby zespolonej określamy tak samo
jak potęgę liczby rzeczywistej. Jeśli „z” jest liczbą zespoloną n, p i q liczbą naturalną, to:
z1 = z,
zn + 1 = zn · z,
z0 = 1,
z -n =
,
z p · z q = z p + q,
z p : z q = z p – q,
(z p)q = z pq
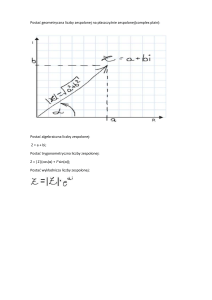
Interpretacja geometryczna liczby zespolonej z = a + bi
rys. 1.
Między punktami płaszczyzny a liczbami zespolonymi zachodzi odpowiedniość, na mocy której
punktowi M o współrzędnych (a,b) piszemy M (a,b) odpowiada liczba zespolona a + bi i liczbie a +
bi,
gdzie
a
i
b
są
liczbami
rzeczywistymi
odpowiada
punkt
o współrzędnych (a, b) rys. 1. Dla dowolnej liczby zespolonej z = a + bi liczby a i b nazywamy
odpowiednio jej częścią rzeczywistą i częścią urojoną. Oznaczamy je rez oraz imz, zatem
re z = a,
im z = b
Liczbę zespoloną i nazywamy jednostką urojoną.
Liczby postaci bi, gdzie b jest liczbą rzeczywistą nazywamy liczbami urojonymi.
Oś OX nazywa się osią rzeczywistą, oś OY osią urojoną.
Moduł liczby zespolonej. Liczby sprzężone.
Właściwości modułu i liczb sprężonych.
rys. 2.
Definicja
Modułem liczby zespolonej z = a + bi nazywamy liczbę rzeczywistą nieujemną i oznaczamy ją
Moduł liczby z równa się odległości punktu z od początku układu współrzędnych.
Wniosek: Dla każdego z jest
rez
,
imz
Przykład
Oblicz moduł liczby zespolonej z = 3 – 4i
Niech z = a + bi
Przyjmijmy oznaczenie
= a – bi
(1)
Definicja
Liczbę
określoną wzorem (1) nazywamy liczbę sprzężoną do danej liczby z.
rys. 3.
Liczby z i
są symetryczne względem osi rzeczywistej.
Własności:
Dla każdej liczby zespolonej z :
=
·z =
2
Twierdzenie
Dla dowolnych liczb zespolonych z1 i z2 jest
;
·
=
;
=
0
Twierdzenie
Dla dowolnych liczb zespolonych z1 i z2
a)
=
b)
=
·
,
,
...
Plik z chomika:
martinoo88k
Inne pliki z tego folderu:


Mathcad v14.0.rar (85639 KB)
Mathcad 14.iso (368314 KB)
 liczby_zespolone_teoria.doc (94 KB)
 Lczby_zespolone.doc (1850 KB)
 liczby.ppt (4133 KB)
Inne foldery tego chomika:
Zgłoś jeśli naruszono regulamin







Strona główna
Aktualności
Kontakt
Dla Mediów
Dział Pomocy
Opinie
Program partnerski




Regulamin serwisu
Polityka prywatności
Ochrona praw autorskich
Platforma wydawców
Copyright © 2012 Chomikuj.pl