19_zespolone

Ciało liczb zespolonych. Interpretacja geometryczna liczby zespolonej, postać
trygonometryczna liczby zespolonej, działania na liczbach zespolonych, pierwiastki z
jedności. Podstawowe twierdzenie algebry.
Paweł Krakowiak
Łukasz Blaźniak
1. Ciało liczb zespolonych.
Definicja 1.
Element 𝑖 = (0,1) ∈ ℂ nazywamy jednostką urojoną.
𝑖 2 = (0,1)(0,1) = (0 ∙ 0 − 1 ∙ 1,0 ∙ 1 + 1 ∙ 0) = (−1,0) = −1
Każdą liczbę zespoloną 𝑧 = (𝑥, 𝑦) można zapisać w postać kanonicznej 𝑧 = 𝑥 + 𝑦𝑖.
Liczby rzeczywiste x oraz y nazywamy odpowiednio częścią rzeczywistą oraz częścią urojoną.
Oznaczamy 𝑥 = 𝑅𝑒 𝑧, 𝑦 = 𝐼𝑚 𝑧.
Definicja 2.
Dla liczby zespolonej 𝑧 = 𝑥 + 𝑦𝑖 liczbę rzeczywistą |𝑧| = √𝑥 2 + 𝑦 2 nazywamy modułem, a liczbę zespoloną
𝑧̅ = 𝑥 − 𝑦𝑖 = 𝑥 + (−𝑦)𝑖 nazywamy sprzężeniem liczby z.
Definicja 3.
Zbiór ℂ = ℝ 𝑥 ℝ wraz z działaniami określonymi wzorami:
 (𝑥, 𝑦) + (𝑥 ′ , 𝑦 ′ ) = (𝑥 + 𝑥 ′ , 𝑦 + 𝑦 ′ )
 (𝑥, 𝑦)(𝑥 ′ , 𝑦 ′ ) = (𝑥 + 𝑦𝑖)(𝑥 ′ + 𝑦 ′ 𝑖) = 𝑥𝑥 ′ + 𝑥𝑦 ′ 𝑖 + 𝑦𝑥 ′ 𝑖 + 𝑦𝑦 ′ 𝑖 2 = 𝑥𝑥 ′ − 𝑦𝑦 ′ + (𝑥𝑦 ′ + 𝑦𝑥 ′ )𝑖 =
(𝑥𝑥 ′ − 𝑦𝑦 ′ , 𝑥𝑦 ′ + 𝑦𝑥 ′ ) 𝑑𝑙𝑎 (𝑥, 𝑦), (𝑥 ′ , 𝑦 ′ ) ∈ ℂ
Stanowi ciało nazywane ciałem liczb zespolonych, a jego elementy liczbami zespolonymi.
Zauważmy, że dla (𝑥, 0), (𝑦, 0) ∈ ℂ,
(𝑥, 0) + (𝑦, 0) = (𝑥 + 𝑦, 0); (𝑥, 0)(𝑦, 0) = (𝑥𝑦, 0)
Można więc liczbę zespoloną (𝑥, 0) utożsamić z liczbą rzeczywistą x i w tym sensie można pisać ℝ = ℂ.
Liczbę zespoloną (𝑥, 𝑦) utożsamiamy z (𝑥, 𝑦) ~ 𝑥 + 𝑦𝑖.
Twierdzenie 1.
Zbiór ( ℂ ,+, ∙) stanowi ciało, którego zerem jest element (0,0), a jedynką jest element (1,0)
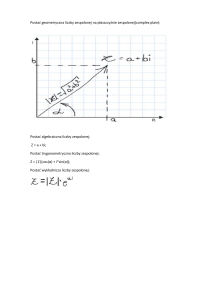
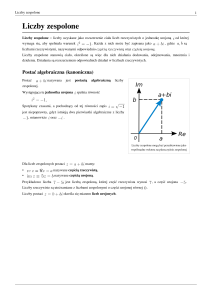
2. Interpretacja geometryczna liczby zespolonej


punkt w układzie współrzędnych to liczba zespolona postaci 𝑧 = 𝑥 + 𝑦𝑖 = (𝑥, 𝑦), gdzie na osi 𝑂𝑋
znajduje się jej część rzeczywista, a na osi 𝑂𝑌 jej część urojona .
dodawanie i odejmowanie liczb zespolonych 𝑧1 , 𝑧2 odpowiada dodawaniu i odejmowaniu wektorów
⃗⃗⃗⃗⃗⃗⃗
𝑂𝑧1 i ⃗⃗⃗⃗⃗⃗⃗
𝑂𝑧2 .


Sprzężenie liczby zespolonej 𝑧 polega na symetrycznym odbiciu liczby zespolonej z względem osi 𝑂𝑋.
Moduł liczby zespolonej 𝑧 jest długością punktu 𝑧 = (𝑥, 𝑦) od początku układu współrzędnych.
Przykład 1. Poniżej kilka liczb zespolonych zaznaczonych na płaszczyźnie zespolonej.
Przykłady:
{𝑧 ∈ ℂ: |𝑧| = 1}
{𝑧 ∈ ℂ: |𝑧| ≤ 1}
3. Własności liczb zespolonych
Twierdzenie 2. Dla 𝑧, 𝑧1 , 𝑧2 ∈ ℂ zachodzą wzory:
𝑧𝑧̅ = |𝑧|2
dowód: niech 𝑧 = 𝑥 + 𝑦𝑖
𝑧𝑧̅ = (𝑥 + 𝑦𝑖)(𝑥 − 𝑦𝑖) = 𝑥 2 − 𝑥𝑦𝑖 − 𝑦 2 𝑖 2 = 𝑥 2 + 𝑦 2 = (√𝑥 2 + 𝑦 2 )2 = |𝑧|2
2. ̅̅̅̅̅̅̅̅̅
𝑧1 ± 𝑧2 = 𝑧̅1 ± 𝑧̅2
dowód: niech 𝑧 = 𝑥 + 𝑦𝑖
̅̅̅̅̅̅̅̅̅
𝑧1 ± 𝑧2 = 𝑥1 ± 𝑥2 − (𝑦1 ± 𝑦2 )𝑖 = (𝑥1 − 𝑦1 𝑖) ± (𝑥2 − 𝑦2 𝑖) = 𝑧̅1 ± 𝑧̅2
3. ̅̅̅̅̅̅
𝑧1 𝑧2 = 𝑧̅1 𝑧̅2
dowód: niech 𝑧 = 𝑥 + 𝑦𝑖
𝑧1 𝑧2 = (𝑥1 𝑥2 − 𝑦1 𝑦2 ) − (𝑥1 𝑦2 − 𝑦1 𝑥2 )𝑖 = (𝑥1 − 𝑦1 𝑖)(𝑥2 − 𝑦2 𝑖) = 𝑧̅1 𝑧̅2
̅̅̅̅̅̅
̅̅̅̅̅
𝑧
𝑧
̅̅̅
4. ( 1) = 1
1.
𝑧2
𝑧
̅̅̅
2
5.
6.
|𝑧1 𝑧2 | = |𝑧1 ||𝑧2 |
7.
8.
|𝑧1 + 𝑧2 | ≤ |𝑧1 | + |𝑧2 |
𝑧+𝑧̅
𝑅𝑒 𝑧 =
𝑧
|𝑧 |
𝑧2
2
| 1| = |𝑧1| o ile 𝑧2 ≠ 0
2
𝑧−𝑧̅
9. 𝐼𝑚 𝑧 =
2𝑖
10. 𝐴𝑟𝑔(𝑧1 𝑧2 ) = 𝐴𝑟𝑔𝑧1 + 𝐴𝑟𝑔𝑧2
4. Postać trygonometryczna liczby zespolonej
Definicja 4. Dla 𝑧 ∈ ℂ\{0} każdą liczbę rzeczywistą 𝜑 taką, że
𝑥
𝑦
𝑐𝑜𝑠𝜑 = |𝑧|
⋀
𝑠𝑖𝑛𝜑 = |𝑧|
nazywamy argumentem liczby z i oznaczamy przez 𝐚𝐫𝐠 𝒛.
Zatem argument liczby zespolonej z to kąt φ wyrażony w mierze łukowej (arg 𝑧 = 𝜑)
Ten spośród argumentów, który leży w przedziale (−𝜋, 𝜋] nazywamy argumentem głównym liczby 𝒛 i
oznaczamy przez 𝐀𝐫𝐠 𝒛.
Definicja 5. Postacią trygonometryczną liczby zespolonej 𝑧 ∈ ℂ\{0} nazywamy jej przedstawienie
𝒛 = |𝒛|(𝒄𝒐𝒔𝝋 + 𝒊𝒔𝒊𝒏𝝋), gdzie 𝜑 = arg 𝑧.
Zbiór ℂ można w sposób naturalny utożsamić z płaszczyzną, na której określiliśmy układ współrzędnych o
początku (0,0) i wersorach (1,0) dla pierwszej osi oraz (0,1) dla drugiej osi. Dla każdej liczby 𝑧 ∈ ℂ\{0} jej
moduł określa odległość punktu z od początku układu, a argument – miarę kąta jaką tworzy wektor 𝑂𝑧 z
dodatnią półosią rzeczywistą.
Twierdzenie 3. Jeżeli 𝑧1 , 𝑧2 ∈ ℂ\{0} oraz 𝜑1 = 𝑎𝑟𝑔𝑧1 , 𝜑2 = 𝑎𝑟𝑔𝑧2 to
1. 𝑧1 𝑧2 = |𝑧1 ||𝑧2 | (cos(𝜑1 + 𝜑2 ) + 𝑖𝑠𝑖𝑛(𝜑1 + 𝜑2 ))
|𝑧 |
𝑧
2. 1 = |𝑧1| (cos(𝜑1 − 𝜑2 ) + 𝑖𝑠𝑖𝑛(𝜑1 − 𝜑2 ))
𝑧2
2
Przykład 2. Wyznaczyć postać trygonometryczną liczby zespolonej 𝑧 = −2 + 2𝑖.
Obliczamy moduł i argument danej liczby
|𝑧| = √(−2)2 + 22 = √8 = 2√2
{
𝑐𝑜𝑠𝜑 =
−√2
2
√2
3
,𝜑= 𝜋
4
𝑠𝑖𝑛𝜑 =
2
Zatem liczba 𝑧 = −2 + 2𝑖 zapisana w postaci trygonometrycznej, to
3
3
𝑧 = √8(𝑐𝑜𝑠 𝜋 + 𝑖𝑠𝑖𝑛 𝜋 )
4
4
5. Potęgowanie i pierwiastkowanie liczb zespolonych, pierwiastki z jedności.
Twierdzenie 4. (Wzór de Moivre’a).
Jeżeli 𝑧 ∈ ℂ\{0} oraz 𝑧 = |𝑧|(𝑐𝑜𝑠𝜑 + 𝑖𝑠𝑖𝑛𝜑), 𝑡𝑜 𝑧 𝑛 = |𝑧|𝑛 (𝑐𝑜𝑠𝑛𝜑 + 𝑖𝑠𝑖𝑛𝑛𝜑).
Przykład 3. |1 + 𝑖| = √2
(1 + 𝑖)1001
𝑐𝑜𝑠𝜑 =
1
√2
, 𝑠𝑖𝑛𝜑 =
1
√2
,𝜑 =
𝜋
4
1001𝜋
1001𝜋
𝜋
𝜋
√2
√2
= √2
(𝑐𝑜𝑠
+ 𝑖𝑠𝑖𝑛
) = 2500 √2 (𝑐𝑜𝑠 + 𝑖𝑠𝑖𝑛 ) = 2500 √2 ( + 𝑖 )
4
4
4
4
2
2
= 2500 (1 + 𝑖)
1001
Definicja 6. Pierwiastkiem n-tego stopnia (gdzie 𝑛 ∈ 𝑁) z liczby zespolonej z nazywamy każdą taką liczbę
𝑛
𝑤 ∈ ℂ, że 𝑤 𝑛 = 𝑧. Oznaczamy √𝑧.
Twierdzenie 5. Dla 𝑧 ∈ ℂ\{0} i 𝑛 ∈ 𝑁 istnieje dokładnie n różnych pierwiastków stopnia n-tego z liczby z.
Pierwiastki n-tego stopnia z liczby 𝑧 = |𝑧|(𝑐𝑜𝑠𝜑 + 𝑖𝑠𝑖𝑛𝜑) wyrażają się wzorami:
𝑛
𝜑+2𝑘𝜋
𝜑+2𝑘𝜋
𝑛
𝑤𝑘 = √|𝑧| (𝑐𝑜𝑠
+ 𝑖𝑠𝑖𝑛
) , 𝑘 = 0,1, … , 𝑛 − 1 , gdzie √ oznacza pierwiastek arytmetyczny dodatni
𝑛
𝑛
stopnia n.
Definicja 7. Liczbę zespoloną z nazywamy pierwiastkiem pierwotnym n-tego stopnia z jedności, jeżeli 𝑧 𝑛 =
1 𝑖 𝑧 𝑠 ≠ 1, dla każdego 𝑠 = 1,2,3, … , 𝑛 − 1.
Np. liczby 𝑖 oraz – 𝑖 są pierwiastkami pierwotnymi czwartego stopnia z jedności, bo 𝑖 4 = 1 oraz (−𝑖)4 = 1, ale
𝑖 3 ≠ 1; natomiast 1 oraz (-1) nie są pierwiastkami pierwotnymi czwartego stopnia z jedności, bo 13 też jest
równy 1 oraz (−1)2 = 1.
Wniosek 1. Pierwiastki n-tego stopnia z jedności (z liczby 1) wyrażają się wzorem:
2𝜋𝑘
2𝜋𝑘
ℇ𝑘 = 𝑐𝑜𝑠
+ 𝑖𝑠𝑖𝑛
, 𝑘 = 0,1, … , 𝑛 − 1
𝑛
𝑛
Przykład 4. Pierwiastki szóstego stopnia z 1
𝑤0 = 1
𝜋
𝜋 1 √3
+ 𝑖𝑠𝑖𝑛 = +
𝑖
3
3 2
2
2𝜋
2𝜋
1 √3
= 𝑐𝑜𝑠
+ 𝑖𝑠𝑖𝑛
=− +
𝑖
3
3
2
2
= 𝑐𝑜𝑠𝜋 + 𝑖𝑠𝑖𝑛𝜋 = −1
4𝜋
4𝜋
1 √3
= 𝑐𝑜𝑠
+ 𝑖𝑠𝑖𝑛
=− −
𝑖
3
3
2
2
5𝜋
5𝜋 1 √3
= 𝑐𝑜𝑠
+ 𝑖𝑠𝑖𝑛
= −
𝑖
3
3
2
2
𝑤1 = 𝑐𝑜𝑠
𝑤2
𝑤3
𝑤4
𝑤5
Twierdzenie 6. (zasadnicze twierdzenie algebry). Każdy wielomian stopnia naturalnego o współczynnikach
zespolonych ma w ciele ℂ liczb zespolonych co najmniej jeden pierwiastek.
(Ciało ℂ jest algebraicznie domknięte)
Przykład 5. Rozwiązać równanie: 𝑥 2 + 1 = 0
Jest to wielomian o współczynnikach rzeczywistych, który nie ma rzeczywistych pierwiastków, a ma pierwiastki
zespolone. 𝑖 2 = −1 ⇒ 𝑖 = √−1
Pierwiastkami powyższego wielomianu są liczby: 𝑥1 = 𝑖, 𝑥2 = −𝑖.
Przykład 6. Rozwiązać równanie kwadratowe: 𝑧 2 − 3𝑧 + 3 + 𝑖 = 0
∆= 9 − 4(3 + 𝑖)
∆= −3 − 4𝑖
√∆= √−3 − 4𝑖
(𝑥 + 𝑦𝑖)2 = −3 − 4𝑖
𝑥 2 + 2𝑥𝑦𝑖 − 𝑦 2 = −3 − 4𝑖
𝑥 2 − 𝑦 2 = −3
{
2𝑥𝑦 = −4
𝑥 2 − 𝑦 2 = −3
2
{
𝑥𝑦 = −2 ⇒ 𝑦 = −
𝑥
2
2
𝑥 2 − (− ) = −3
𝑥
4
2
𝑥 − 2 = −3
𝑥
𝑥 4 + 3𝑥 2 − 4 = 0
𝑡 = 𝑥2 , 𝑡 ≥ 0
𝑡 2 + 3𝑡 − 4 = 0
∆= 9 + 16 = 25
√∆= 5
𝑡1 = −4 𝑠𝑝𝑟𝑧𝑒𝑐𝑧𝑛𝑜𝑠ć!
𝑡2 = 1
𝑥2 = 1
𝑥=1
{
⋁
𝑦 = −2
𝑧1 = 1 − 2𝑖
𝑧2 = −1 + 2𝑖
𝑥 = −1
{
𝑦=2
√∆= 1 − 2𝑖
3−(1−2𝑖)
2+2𝑖
𝑧1 =
=
= 1+𝑖
2
2
𝑧2 =
3+(1−2𝑖)
2
=
4−2𝑖
2
= 2−𝑖