Obwód szeregowy RLC

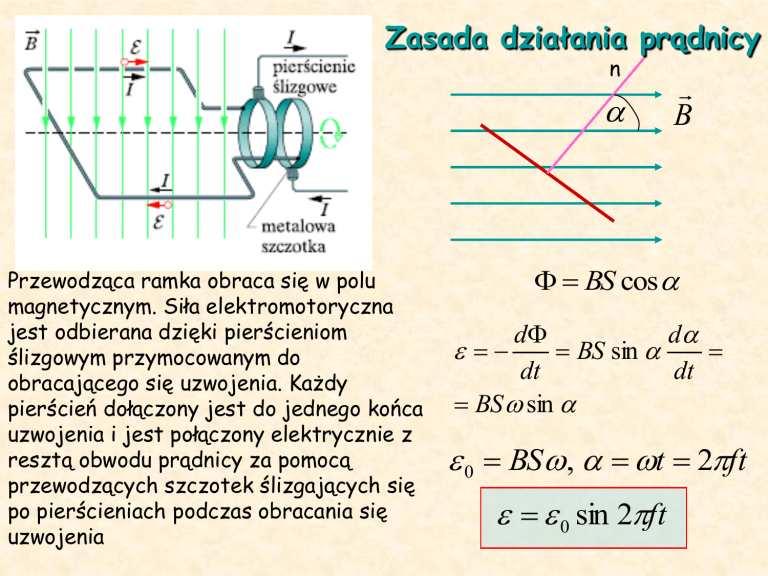
Zasada działania prądnicy
n

Przewodząca ramka obraca się w polu
magnetycznym. Siła elektromotoryczna
jest odbierana dzięki pierścieniom
ślizgowym przymocowanym do
obracającego się uzwojenia. Każdy
pierścień dołączony jest do jednego końca
uzwojenia i jest połączony elektrycznie z
resztą obwodu prądnicy za pomocą
przewodzących szczotek ślizgających się
po pierścieniach podczas obracania się
uzwojenia

B
  BS cos
d
d
 
 BS sin 

dt
dt
 BS  sin 
 0  BS,   t  2ft
   0 sin 2ft
Prądy przemienne
3
I(t)
(t)
2
(t), I(t)
1
0
-1


-2
-3
0
20
40
t
60
80
100
W obwodzie zewnętrznym, do którego przyłożone jest napięcie
U  U 0 sin t
płynie prąd o natężeniu
 
I  I 0 sin( t   )  I 0 sin   t  
 
Obwody prądu przemiennego
Obwód drgający RLC
I
U
W chwili t ładunek na kondensatorze = Q,
różnica potencjałów U
I 
dQ
dI
, Q  CU , U  L  RI
dt
dt
dU
I  C
,
dt
d 2U
dU
U   LC 2  RC
dt
dt
Otrzymujemy równanie różniczkowe
d 2U R dU
1


U 0
2
dt
L dt LC
przewidujemy rozwiązanie w postaci
U  Ae   t cos t
i wstawiamy go do równania różniczkowego
U  Ae   t cos t
d 2U R dU
1


U 0
2
dt
L dt LC
dU
  Ae   t cos  t  Ae   t sin  t
dt


d2 U
 t
2
2

Ae



cos  t  2 sin  t
2
dt



Ae   t  2   2 cos  t  2 sin  t 


R  t
Ae   cos  t   sin  t  
L
1
Ae   t cos  t  0
LC

2


  2 cos  t  2 sin  t 

R
  cos  t   sin  t   1 cos  t  0
L
LC

R
1 
R 
 2

2
     L   LC  cos  t  2   L   sin  t  0
=0
=0

2

2 
R
1

0
L
LC
2 
R
 0
L

R2
R2
1
2
  2 
0
2
4L
2 L LC
R
2L
1
R2
 
 2
LC 4 L
2
Stała ω jest liczbą rzeczywistą, musi być spełniony warunek
2
1
R
2 
 2 0
LC 4 L
Rozwiązanie równania
ma postać
R2
1

4 L2 LC
d 2U R dU
1


U 0
2
dt
L dt LC
U  Ae   t cos t
jeśli jest spełniony warunek
2
d
U R dU
1
Rozwiązaniem równania różniczkowego


U 0
2
dt
L dt LC
może być również funkcja
U  Be   t sin t
Ogólne rozwiązanie możemy zapisać w postaci
U  e   t  A cos t  B sin t 
Kondensator został naładowany,
następnie odłączony od źródła
zasilania i połączony z cewką –
występują drgania sinusoidalne
tłumione
0,3
0,2
0,1
U
0,0
-0,1
-0,2
-0,3
-0,4
0
50
100
t
150
200
 t
U

Ae
cos t. Natężenie prądu płynącego w obwodzie
Załóżmy, że


dU
I  C
 C  Ae  t cos t  Ae t sin t 
dt


 CA  cos t  sin t e  t


Wielkość / jest miarą tłumienia,
dla małych wartości składnik
zawierający cost powoduje zmianę
fazy o kąt równy arctg(/)
0,3
 /   0,5
0,2
0,1
I
0,0
-0,1
 /   0,05
-0,2
U, I
0,3
-0,3
0,2
-0,4
0,1
0
50
100
150
200
0,0
U, I
t
Oscylacje natężenia prądu są
przesunięte w fazie
względem oscylacji napięcia
-0,1
-0,2
-0,3
-0,4
0
50
100
t
150
200
Oscylacje powodują ciągłe przekazywanie energii między kondensatorem
a cewką
energia pola elektrycznego
1
0,3
0,1
U, I
0,0
4
2
-0,1
-0,2
3
-0,3
1
1
0,2
2
4
3
energia pola magnetycznego
1
2
+
4
-
3

E
I
2

B
-0,4
0
50
t
3
+

E
4
I

B
Pokazaliśmy, że dla obwodu RLC w przypadku słabego tłumienia (mały
opór), spełniony jest warunek
R2
1

4 L2 LC
L
R2
C
R 2
Obwód jest przetłumiony. Rozwiązanie równania
d 2U R dU
1


U 0
2
dt
L dt LC
ma postać
lub ogólną
L
C
U  Ae  t
U  Ae 1 t1  Be   2 t2
Nie ma wówczas drgań, a tylko monotoniczny spadek napięcia.
U  U 0e

R
t
2L
L  10 4 H , C  10 8 F , U 0  5V
1
R2
cos
 2t
LC 4 L
-2
Drgania zanikające:
krzywe zaczynają się w tym samym punkcie
przy R = 200  - tłumienie krytyczne:
1
 10 4 108  1012
LC
R2
200 2
12


10
4 L2 4 10 8
-4
przy R = 600  - przetłumienie
6
20
60 
200 
600 
4
U [V]
2
0
0,0
-6
2,0x10
-6
-6
4,0x10
6,0x10
-6
8,0x10
-5
1,0x10
t [s]
Jeśli R = 0 – oscylator nietłumiony. Częstość drgań własnych takiego
oscylatora

1
R2
 2
LC 4 L
o 
1
LC
Prąd przemienny
II prawo Kirchhoffa
L
dI
 IR   o cos t
dt
I  I o cos( t   )
 LI o sin( t   )  I o R cos(t   )   o cos t
Obwód szeregowy RL
 LI osin t cos   cos t sin    I o Rcos t cos   sin t sin     o cos t  0
I o R cos   LI osin    o  0
 I o R sin   LI ocos   0
L
tg  
R
Io R
cos  
1
 L
2 2
R
2
 LI o
1
L
R
1
tg   1
2
1
 L
2 2
R
2
, sin   tg   cos 
 o  0
1
L
R
Io R
 LI o
 o  0
2 2
2
2
2
2
R  L R
 L R
R
I o R 2  I o L2 2   o  2 L2  R 2  0

o
 2 L2  R 2
Io   o 2 2 2 
R  L    2 L2  R 2

I o R 2  L2 2   o  2 L2  R 2
I
o
R L
2
2
2
cos( t   )
I
o

 L 
cos  t  arctg  

2
2 2
R


R L

I
o

 L 
cos  t  arctg  

2
2 2
R


R L

6
4
I
2
 o  5V ,   314rad / s, R  20, L  2 10 3 H
0
-2
-4
-6
0
20
40
t
Z
o
Io
 R2  L22
Prąd jest opóźniony w fazie względem
siły elektromotorycznej.
Wielkość L – nazywamy oporem
indukcyjnym
jest oporem całkowitym
Obwód szeregowy RC
IR 
Q
  o cos  t
C
dQ
I 
dt
I  I o cos(t   )
Q    Idt  
RI o cos( t   ) 
Io

sin( t   )
Io
sin(  t   )   o cos  t
C
Postępując podobnie jak poprzednio, otrzymamy:
1
tg 
RC 
Io 
I
o
1
R  2 2
C
2
o
1
2
R  2 2
C
cos( t   )
Z
o
Io
 R2 
1
 2C 2
0,006
W obwodzie zawierającym pojemność
natężenie prądu wyprzedza napięcie.
0,004
I
0,002
0,000
Uwaga: rozważamy rozwiązania stacjonarne !
-0,002
-0,004
Obwód szeregowy RLC
-0,006
0
20
40
t
W obwodzie płynie prąd o natężeniu
I  I o cos(t   )
Spadek potencjału na cewce
dI
U L  L
  I oL sin( t   )
dt
Spadek potencjału na kondensatorze
Io
Q
1
U C      Idt 
sin( t   )
C
C
C
Suma spadków napięć:
Io
U L  U LC   I oL sin( t   ) 
sin( t   ) 
C
1 

  L 
 I o sin( t   )
C 

Jeśli w obwodzie istnieje niezerowy opór omowy, to
1 

Z  R   L 

C 

2
2
I
o
1 

R   L 

C 

2
2
cos(t   )
tg 
1
RC

L
R
5,5
6
20
60 
200 
4
20 
60 
400 
5,0
4,5
4,0
3,5
2
3,0
Io
2,0
0
1,5
1,0
-2
0,5
0,0
-4
-0,5
0
0,0
-6
2,0x10
-6
-6
4,0x10
6,0x10
-6
8,0x10
6
1x10
6
6
2x10
6
3x10
4x10
6
5x10

-5
1,0x10
t [s]
80
20 
60 
200 
60
40
20
0

U [V]
2,5
-20
-40
-60
-80
0,0
6
6
2,0x10
4,0x10

6
6,0x10
Moc prądu przemiennego
U  U 0 sin t
I  I 0 sin( t   )
Praca elementarna prądu
dW  UIdt  U 0 sin t I 0 sin( t   )dt
a moc chwilowa
U 02
dW
2
P
 U 0 I 0 sin t sin( t  
)

sin
t

dt
R
0
Przesuniecie fazowe między natężeniem prądu a napięciem
zależy od elementów wchodzących w skład obwodu elektrycznego
Praca wykonana w ciągu okresu
T
T
0
0
W   dW  U 0 I 0  sin t sin( t   )dt
 2 sin
 
2
sin
 
2
 cos   cos 
2 sin t sin( t   )  cos   cos( 2t   )
T
U0I0
W  U 0 I 0  sin t sin( t   )dt 
2
0
U0I0

2
T
T
 cos   cos(2t   )dt 
0
U0 I0
1


t cos   2 sin( 2t   )  2 T cos   U sk I skT cos 

0
Moc prądu zmiennego
W
P
 U sk I sk cos 
T
U sk I sk
- moc pozorna
cos 
- współczynnik mocy
Energia rozproszona w obwodzie wydzieli się na oporze R.
Przyrządy mierzą tzw. wartości
skuteczne.
Wartości skuteczne
4
I o2
2
I
I sk2
Natężenie skuteczne – takie
natężenie prądu stałego, który
wydziela w tym samym czasie
taką samą ilość energii co dany
prąd zmienny.
0
-2
0
1
t
2
Pole zawarte pod krzywą I o2 (t )
jest wartością ciepła
wydzielonego przez prąd
zmienny w oporniku 1  w ciągu
jednego okresu
Taką samą ilość ciepła wydzieli prąd o natężeniu Isk jeżeli powierzchnia
2
prostokąta I skT będzie równa powierzchni zakreskowanej
T
T
1
S   I sin tdt I  (1  cos 2t )dt 
2
0
0
2
0
2 T
0
I

2
2
2
0
2 T
0
2
0
I
I
0 dt  2 0 cos 2tdt  2
T
1


t

sin
2

t


 2
0
I 02 
T
2  I 02
 T 
sin 2
T   T  I sk2 T
2
2  2
T  2
cos 2  cos 2   sin 2  
 1  sin 2   sin 2   1  2 sin 2 
1
sin   (1  cos 2 )
2
2
I0
I sk 
2
Podobnie otrzymamy
U0
U sk 
2
Napięcie skuteczne w sieci wynosi 230 V. Amplituda napięcia
U 0  U sk 2  230 2  325V
Jeśli włączymy w obwód żarówkę o mocy 100 W to natężenie
skuteczne prądu wynosi
P  UI
P 100W
I sk 

 0,43 A
U sk 230V
a amplituda natężenia prądu płynącego przez żarówkę
I 0  I sk 2  0,43 2  0,62 A