Sprawdzanie jakości związku regresyjnego.
6.1 Estymacja wariancji składnika losowego.
Przypomnijmy, że przez
oznaczamy wariancję składnika (błędu) losowego w modelu
regresji. Z założenia wariancja jest jednakowa dla wszystkich obserwacji.
Wariancję składnika losowego
uważa się za miarę rozproszenia obserwacji wokół
"powierzchni" regresji. "Powierzchnią" regresji nazywamy zbiór wszystkich wartości
teoretycznych w modelu regresji. Dla jest to prosta, a dla płaszczyzna. Ogólnie mówiąc, im
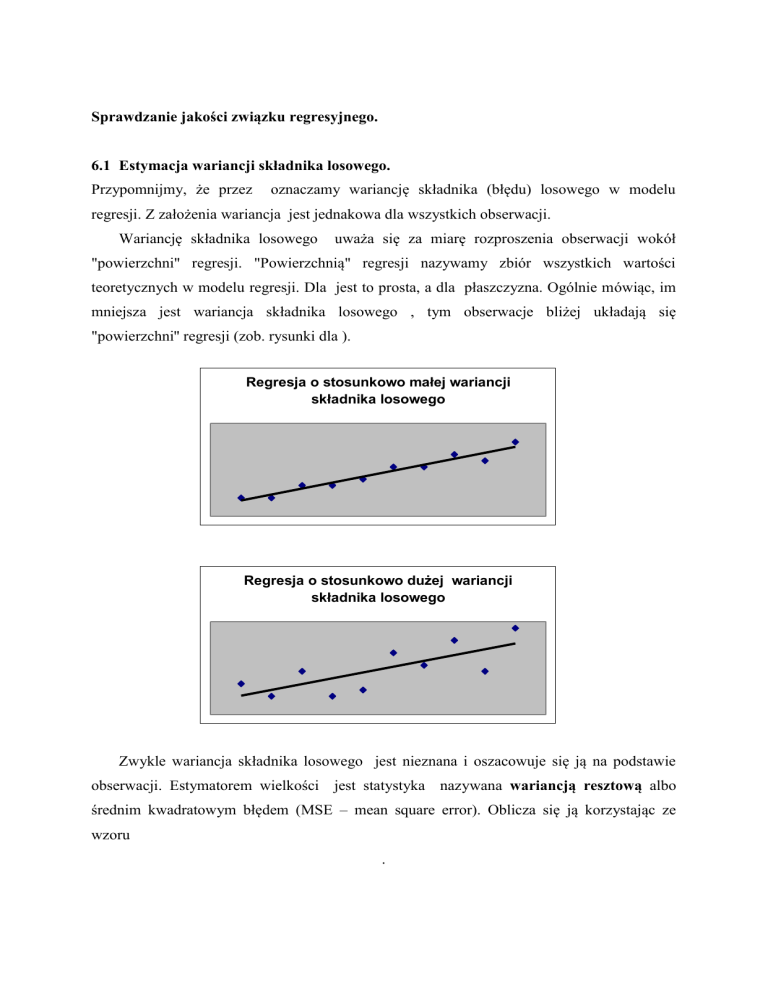
mniejsza jest wariancja składnika losowego , tym obserwacje bliżej układają się
"powierzchni'' regresji (zob. rysunki dla ).
Regresja o stosunkowo małej wariancji
składnika losowego
Regresja o stosunkowo dużej wariancji
składnika losowego
Zwykle wariancja składnika losowego jest nieznana i oszacowuje się ją na podstawie
obserwacji. Estymatorem wielkości jest statystyka nazywana wariancją resztową albo
średnim kwadratowym błędem (MSE – mean square error). Oblicza się ją korzystając ze
wzoru
.
Pierwiastek kwadratowy nazywa się standardowym błędem (szacunku).
Przykład 6.1 (Inflacja 2000) (kontynuacja przykładu 5.1). W szczególnym przypadku
korzystamy ze wzorów
,
Ponieważ , i , więc , oraz .
Przykład 6.2 (Reklama).(kontynuacja przykładu 5.2).
Z wydruku
PODSUMOWANIE - WYJŚCIE
Statystyki regresji
Wielokrotność R
R kwadrat
Dopasowany R kwadrat
Błąd standardowy
Obserwacje
0,980326
0,96104
0,949908
1,91094
10
ANALIZA WARIANCJI
df
Regresja
Resztkowy
Razem
odczytujemy
SS
MS
F
Istotność F
2 630,5381 315,2691 86,33504
1,17E-05
7 25,56185 3,651693
9
656,1
oraz .
6.2 Współczynnik determinacji.
Średni błąd kwadratowy zależy od wymiaru (jednostki) danych, w jednych sytuacjach ta
sama wartość liczbowa błędu może być uznana za małą, a w innych za dużą. Potrzebujemy
więc miary (względnej), która pozwalałaby na porównanie dopasowania do danych różnych
modeli. Taką miarą jest współczynnik determinacji .
Współczynnik determinacji
jest opisową miarą dopasowania modelu regresji do
danych, czyli miarą siły liniowego związku między danymi. Mierzy on część zmienności
zmiennej objaśnianej y, która została wyjaśniona liniowym oddziaływaniem zmiennych
objaśniających . Oblicza się go ze wzoru
.
Współczynnik determinacji przyjmuje wartości z zakresu od 0 do 1. Przy czym, gdy
- dane leżą dokładnie na "płaszczyźnie" regresji (zmienność jest wyjaśniona w 100 %);
- regresja niczego nie wyjaśnia, dane są nieskorelowane;
- "płaszczyzna" regresji jest tym lepiej dopasowana do danych, im współczynnik
determinacji jest bliższy jedności.
Można, na przykład, przyjąć następującą interpretację:
(1)
-
dopasowanie bardzo dobre,
(2)
-
dopasowanie dobre,
(3)
-
dopasowanie zadawalające w niektórych zastosowaniach.
Zwróćmy także uwagę, ze mówimy, np.: "regresja wyjaśnia 93 % zmienności, gdy ".
Zwiększenie liczby k zmiennych objaśniających zwiększa wartość współczynnika
determinacji , gdyż jest on niemalejącą funkcją liczby zmiennych objaśniających. Utrudnia to
porównywanie modeli regresji w oparciu o wartości współczynnika . Wprowadzono więc tzw.
skorygowany współczynnik determinacji, który nie ma tej wady. Definiuje siego wzorem
Skorygowany współczynnik determinacji wykorzystuje się w przypadku porównywania
modeli regresji opartych o te same dane statystyczne, ale zawierających różne liczby
zmiennych objaśniających.
Przykład 6.1 (Inflacja 2000) (kontynuacja). W szczególnym przypadku , współczynnik
determinacji oblicz się ze wzoru
.
Ponieważ , , , więc
.
Regresja wyjaśnia prawie 97 % zmienności, dopasowanie modelu jest więc bardzo dobre.
W przypadku skorygowany współczynnik determinacji jest równy współczynnikowi
determinacji .
Przykład 6.2 (Reklama).(kontynuacja przykładu 5.2).
Z wydruku
Statystyki regresji
Wielokrotność R
R kwadrat
Dopasowany R kwadrat
Błąd standardowy
Obserwacje
0,980326
0,96104
0,949908
1,91094
10
odczytujemy
oraz .
Regresja wyjaśnia 96 % zmienności, dopasowanie modelu jest więc bardzo dobre.