Wyznaczanie modułu sprężystości za pomocą

ĆWICZENIE 2
Wyznaczanie modułu sprężystości
za pomocą wahadła torsyjnego
Obowiązkowa znajomość zagadnień
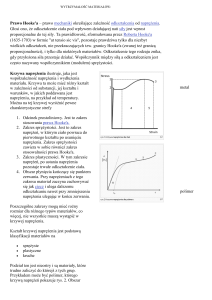
Charakterystyka odkształceń sprężystych, pojęcie naprężenia. Prawo Hooke’a,
moduł Kirchhoffa i jego wpływ na sprężystość materiałów. Budowa i zastosowania
wahadła torsyjnego. Okres drgań, moment bezwładności, twierdzenie Steinera. Istota
pomiaru modułu sprężystości postaciowej za pomocą wahadła torsyjnego. Znajomość
jednostek w układzie SI (jednostki pochodne i wtórne).
Zadania do wykonania
I. Poznanie podstaw teoretycznych zjawiska odkształceń sprężystych, ze szczególnym
uwzględnieniem ścinania prostego.
II. Poznanie budowy i zastosowań wahadła torsyjnego.
III. Wykonanie pomiarów okresów drgań wahadła torsyjnego dla prętów z różnych
materiałów (wraz z pomiarami uzupełniającymi).
IV. Zestawienie wyników i obliczenie wartości modułu sprężystości postaciowej
różnych materiałów.
Wiadomości wprowadzające
Siły zewnętrzne działając na element powodują jego odkształcenie, które może być:
 sprężyste, jeżeli po usunięciu czynnika wywołującego naprężenie ciało powraca do
kształtu pierwotnego,
 plastyczne (trwałe), jeżeli po usunięciu czynnika wywołującego, ciało nie powraca
do kształtu pierwotnego.
Poszczególne elementy konstrukcyjne w czasie pracy przenoszą pewne obciążenia.
Zbyt duże obciążenia mogą doprowadzić do utraty spójności cząstek materiału, czego
wynikiem mogą być pęknięcia danego ciała. Siła zewnętrzna przyłożona statycznie lub
dynamicznie, skupiona lub rozłożona, powoduje powstanie w ciele sił wewnętrznych
działających na umowny przekrój. Wypadkowa sił nosi nazwę siły napięcia danego
przekroju. Siła napięcia przypadająca na jednostkę powierzchni danego przekroju
nazywa się naprężeniem. Podstawową jednostką naprężenia jest Pascal (Pa = N/m2).
Rozważmy przypadek, gdy siły działające na ciało powodują jego odkształcenie
sprężyste, a więc takie, gdy deformacja znika po ustąpieniu siły odkształcającej F. W
zależności od kąta między wektorem siły działającej a powierzchnią ciała
odkształconego, rozróżniamy siły normalne FN, tj. działające prostopadłe do
1
ĆWICZENIE 2
powierzchni (ściskające), oraz siły styczne do powierzchni (ścinające), FS (rys. 1).
Takimi właśnie siłami zajmować się będziemy w naszym ćwiczeniu.
Rys. 1. Odkształcenie prostopadłościanu pod wpływem sił stycznych
Naprężenie styczne τ – jest to stosunek siły stycznej FS do powierzchni S, na którą
ta siła działa:
(1)
Efekt działania takiego naprężenia nazywamy ścinaniem prostym. Odkształcenie
mierzy się wtedy za pomocą tzw. kąta ścinania γ tj. kąta jaki tworzy płaszczyzna
pierwotna z płaszczyzną obróconą na skutek ścinania (rys. 1). Między wielkościami γ
oraz τ zachodzi związek znany jako prawo Hooke’a (które mówi, że odkształcenie ciała
pod wpływem działającej na niego siły jest wprost proporcjonalne do tej siły), które
przyjmuje postać:
(2)
Współczynnik G – zwany modułem sztywności, modułem sprężystości postaciowej
lub modułem Kirchhoffa ma wymiar N/m2 = Pa. Charakteryzuje on własności sprężyste
materiału. Im jest większy, tym trudniej jest zmienić kształt ciała. Wartości jego wahają
się od 1,5·106 Pa dla gumy miękkiej, do ok. 8,5·1010 Pa dla stali. Materiały o niskiej
wartości modułu sprężystości wykorzystywane są na elementy sprężyste, tj. sprężyny,
podkładki sprężyste itp. Materiały o wysokim module wykorzystywane są tam, gdzie
odkształcenia sprężyste są niepożądane, a wysoka sztywność materiału konstrukcyjnego
jest konieczna np. korpusy i elementy obrabiarek.
Naprężenia styczne występują także w skręcanym pręcie, a więc skręcanie jest
szczególnym przypadkiem ścinania materiału (rys. 2).
Dla uproszczenia w obliczeniach wytrzymałościowych przyjmuje się przeważnie, że
rozpatrywane tworzywo jest ośrodkiem jednorodnym i izotropowym (ciało, które we
wszystkich kierunkach ma jednakowe własności). Anizotropię uwzględnia się jednak
koniecznie w przypadku stosowania drewna oraz tworzyw sztucznych zbrojonych
(laminatów).
2
ĆWICZENIE 2
Rys. 2. Odkształcanie elementów skręcanego pręta
Wahadło torsyjne
W wahadle grawitacyjnym moment kierujący wytwarza siła ciężkości. W wahadle
torsyjnym powoduje go siła sprężystości pochodząca od skręconego pręta lub innego
ciała sprężystego. Wahadłem torsyjnym jest m.in. balans, stosowany jako podstawowy
element odmierzający czas w mechanicznych zegarkach ręcznych i kieszonkowych oraz
w większości zegarów stołowych (rys. 3). W odróżnieniu od stosowanego w innych
zegarach wahadła fizycznego, ruch balansu nie jest związany z obecnością pola
grawitacyjnego Ziemi. Może on zatem pracować niezależnie od ustawienia względem
pionu, a jego okres ruchu jest niezależny od miejsca na Ziemi.
a)
b)
Rys. 3. a) Zegar stołowy z wahadłem torsyjnym (widocznym pod tarczą zegara);
b) zegar z wahadłem fizycznym.
3
ĆWICZENIE 2
Po odkształceniu ciała sprężystego o kąt α od położenia równowagi powstają w nim
drgania pod wpływem momentu siły skręcającej: M = – Dα zwracającego ciało zawsze
do położenia równowagi. Współczynnik proporcjonalności D, nazywamy momentem
kierującym jest równy:
(3)
gdzie:
r – promień skręcanego pręta,
L – długość skręcanego pręta.
Okres drgań takiego układu (a więc najkrótszy czas po jakim wychylenie, prędkość
i przyśpieszenie przyjmą tę samą wartość) wyraża się wzorem:
√
√
(4)
gdzie:
I – momentem bezwładności masy wprawionej w drgania względem osi przechodzącej
przez oś pręta.
Moment bezwładności I jest miara bezwładności ciała w ruchu obrotowym
względem wybranej osi obrotu. Im większy moment, tym trudniej zmienić ruch
obrotowy ciała, np. rozkręcić dane ciało lub zmniejszyć jego prędkość kątową. Moment
bezwładności odgrywa taką samą rolę w dynamice ruchu obrotowego jak masa w
dynamice ruchu postępowego. Moment bezwładności zależy od osi obrotu ciała.
Moment bezwładności ciała składającego się z n punktów materialnych jest sumą
momentów bezwładności wszystkich tych punktów względem obranej osi obrotu:
∑
(5)
Moment bezwładności ciała zależy od wyboru osi obrotu, od kształtu ciała i od
rozmieszczenia masy w ciele. Zwykle mierzy się go w kg·m².
Dla ciał o ciągłym rozkładzie masy sumowanie we wzorze na moment bezwładności
przechodzi w całkowanie. Niech ciało będzie podzielone na nieskończenie małe
elementy o masach dm, oraz niech r oznacza odległość każdego takiego elementu od osi
obrotu. W takim przypadku moment bezwładności określa wzór:
∫
(6)
4
ĆWICZENIE 2
gdzie całkowanie odbywa się po całej objętości V ciała.
Twierdzenie Steinera mówi, że moment bezwładności I bryły względem dowolnej
osi (np. O’1O’2 patrz Rys. 4) równy jest momentowi bezwładności tej bryły względem
osi przechodzącej przez jej środek ciężkości (oś O1O2 patrz Rys. 4) i równoległej do
danej osi, powiększonemu o iloczyn masy tej bryły przez kwadrat odległości między
osiami a:
(7)
gdzie: IS – moment bezwładności wahadła względem osi przechodzącej przez środek
ciężkości;
a – odległości między osiami.
Rys. 4. Ciało obracające się względem osi O’1O’2, oś O1O2 jest osią przechodzącą przez
środek ciężkości.
Przekształcając to wyrażenie na T znajdujemy wartość modułu sprężystości:
(8)
Moduł sprężystości wyznaczyć możemy doświadczalnie wywołując drgania
torsyjne, posługując się prostym przyrządem pokazanym na rys. 5.
Badany pręt o długości L, zamocowany sztywno w uchwycie obciążony jest
wibratorem, na którym możemy umieszczać ciężarki. Skręcenie wibratora o niewielki
kąt powoduje powstanie w pręcie sił sprężystości, które wywołują drgania harmoniczne
całego układu. Wszystkie wielkości występujące we wzorze do obliczenia modułu
sprężystości G, poza momentem bezwładności I, możemy łatwo zmierzyć. Wyznaczenie
momentu bezwładności takiej bryły, jaką jest wibrator, byłoby rzeczą bardzo
5
ĆWICZENIE 2
skomplikowaną. Trudność tę omijamy w następujący sposób. W pierwszej fazie
doświadczenia wprawiamy w ruch wibrator nie obciążony lub umieszczamy na nim
ciężarki dające „obciążenie wstępne” (które należy traktować jako wchodzące w skład
masy nieobciążonego wibratora) i znajdujemy okres drgań takiego układu:
Rys. 5. Laboratoryjny model wahadła torsyjnego
√
(9)
Następnie umieszczamy na wibratorze dodatkowe ciężarki (np. w kształcie walca),
których moment bezwładności względem osi przechodzącej przez ich środek masy
możemy łatwo wyznaczyć (ewentualnie odczytać z tablic) i mierzymy nowy okres drgań
T2:
√
(10)
Odejmując od T2 wartość T1 (a więc rozpatrując moment bezwładności pochodzący
tylko od dodatkowych ciężarków) i podstawiając wartość D z wcześniejszej zależności
oraz przekształcając równanie otrzymujemy:
6
ĆWICZENIE 2
(
)
(11)
Jeżeli to dodatkowe obciążenie stanowią jednorodne walce (w ilości n) o momencie
bezwładności względem osi przechodzącej przez ich środek ciężkości i równoległej do
osi pręta wynoszącym I0 = mR2 (m – jest masą walca, R – jego promieniem), i gdy
walce te umieścimy w odległości d od osi pręta, to zgodnie z twierdzeniem Steinera:
(
)
(
)
(12)
Moduł sprężystości wyznaczamy ze wzoru na G po podstawieniu do niego
wyrażenia na Iz otrzymujemy:
( ̅
̅ (
̅ )̅
)
(13)
Jak widać z powyższych zależności – znając moduł sprężystości postaciowej,
możliwe jest (korzystając z wahadła torsyjnego) wyznaczenie momentów bezwładności
skomplikowanych (nieregularnych) brył.
Kreseczka nad wielkością oznacza wartość średnią np.: ̅ średnia masa wszystkich
odważników.
Wykonanie ćwiczenia i opracowanie wyników
1. Za pomocą suwmiarki mierzymy kilka razy (5÷6) w różnych miejscach średnicę
badanego pręta (2r).
2. Mierzymy liniałem czynną długość badanego pręta (L) – miejscami pomiędzy
zaciskami mocującymi pręt.
3. Wprawiamy w ruch wibrator nie obciążony (lub obciążony „obciążeniem
wstępnym”). Mierzymy czas dwudziestu okresów drgań (20T1), pomiar powtarzamy
dwukrotnie.
4. Mierzymy średnice n dodatkowych ciężarków (2R).
5. Ważymy n dodatkowych ciężarków (m) – masa podana na odważnikach.
7
ĆWICZENIE 2
6. Mierzymy odległość między sztyftami na których umieszczamy te ciężarki (2d),
(rys. 5).
7. Po umieszczeniu dwóch, a potem czterech ciężarków na sztyftach ponownie
wprawiamy wibrator w drgania. Mierzymy czas dwudziestu okresów drgań (20T2),
pomiar powtarzamy dwukrotnie.
8. Po wykonaniu odpowiednich pomiarów, wyznaczamy wartość T 1 i T2 oraz
obliczamy wartości średnie: ̅, ̅ , ̅ , ̅ .
Zmierzone wielkości zapisujemy w tabeli:
Badany
materiał
Materiał 1
Materiał 2
Liczba odważników n
2
4
0
2
0
4
2r
̅
L
20T1
T1
2R
̅
m
̅
2d
̅
20T2
T2
9. Wielkość modułu sprężystości postaciowej G obliczamy ze wzoru (13).
10. Powtarzamy pomiary i obliczenia dla pręta wykonanego z innego materiału
(wskazanego przez prowadzącego ćwiczenia).
11. Porównujemy znalezioną wartość G z wartością tablicową (załącznik nr 2). Czy
znaleziona przez nas wielkość zgadza się z wartością tablicową?
12. Proszę wyprowadzić jednostkę współczynnika sprężystości G.
Otrzymane wyniki przedstawiamy w tabeli:
Badany
materiał
Liczba
odważników n
Materiał 1
2
4
2
4
Materiał 2
Wartość G
obliczona
8
Wartość
średnia ̅
z obliczeń
Wartość G
tablicowa
ĆWICZENIE 2
ZAŁĄCZNIK NR 2
Wartości współczynników sprężystości [1011 N/m2]
Materiał
Moduł Younga E
Moduł
sprężystości G
Glin
0,63 – 0,72
0,23 – 0,27
Miedź
0,8 – 1,3
0,39 – 0,48
Mosiądz
0,80 – 1,00
0,27 – 0,37
Ołów
0,15 – 0,17
0,064
Stal
2,00 – 2,20
0,80 – 0,83
Szkło
0,50 – 0,80
0,2 – 0,3
Uniwersytet Rolniczy
Wydział leśny
Katedra Mechanizacji Prac Leśnych
Laboratorium Fizyki – instrukcja do ćwiczeń
Rok akademicki 2012/2013
9