Konecki M., Wpływ szybkości wydzielania ciepła i emisji dymu na

Model strefowy programu komputerowego CFAST
(wybór z pozycji: Konecki M., Wpływ szybkości wydzielania ciepła i emisji dymu na
rozwój pożaru w układzie pomieszczeń, wyd. SGSP, Warszawa (2007).
Program komputerowy CFAST (Consolidated Model of Fire Growth and Smoke Transport)
oparty jest na rozbudowanym deterministycznym modelu strefowym pożaru w układach pomieszczeń
budynku. Jest programem niekomercyjnym, który powstał i jest rozwijany w National Institute of
Standards and Technology (NIST) w USA, wykorzystywanym do badań w wielu ośrodkach na świecie
[1].
Pierwsza wersja 1.0 programu powstała w 1990 r z połączenia i rozszerzenia dwóch wcześniej
powstałych programów, FAST [2] i CCFM.VENTS [3]. Kolejne wersje programu zawierały różne
dodatkowe submodele (człony źródłowe) rozszerzające możliwości i poprawiające dokładność opisu
środowiska pożaru. Programy serii 3.0 – 3.1.7 (lata 1996 – 2001) zawierały m.innymi pionowe
rozprzestrzenianie płomienia, strumień podsufitowy, wiele materiałów palnych w pomieszczeniu i źródeł
pożaru. Wersja 4.0 z 2000 r została wzbogacona o horyzontalny strumień ciepła przewodzony przez
ściany oraz horyzontalny przepływ dymu korytarzu a wersje 5.0 - 5.1.1 (lata 2001-2004) o chemię
spalania i przepływy pionowe.
Wykorzystana w niniejszej pracy ostatnia wersja CFAST 6 z 2006 r. zawiera poprawione
submodele pożaru i przepływów horyzontalnych i jest obecnie programem komputerowym opartym na
najbardziej złożonym modelu strefowym, zakładającym w każdym pomieszczeniu obecność dwóch stref
(górnej gorącej i dolnej chłodnej), a ponadto, w pomieszczeniu ze źródłem ognia, kolumny konwekcyjnej
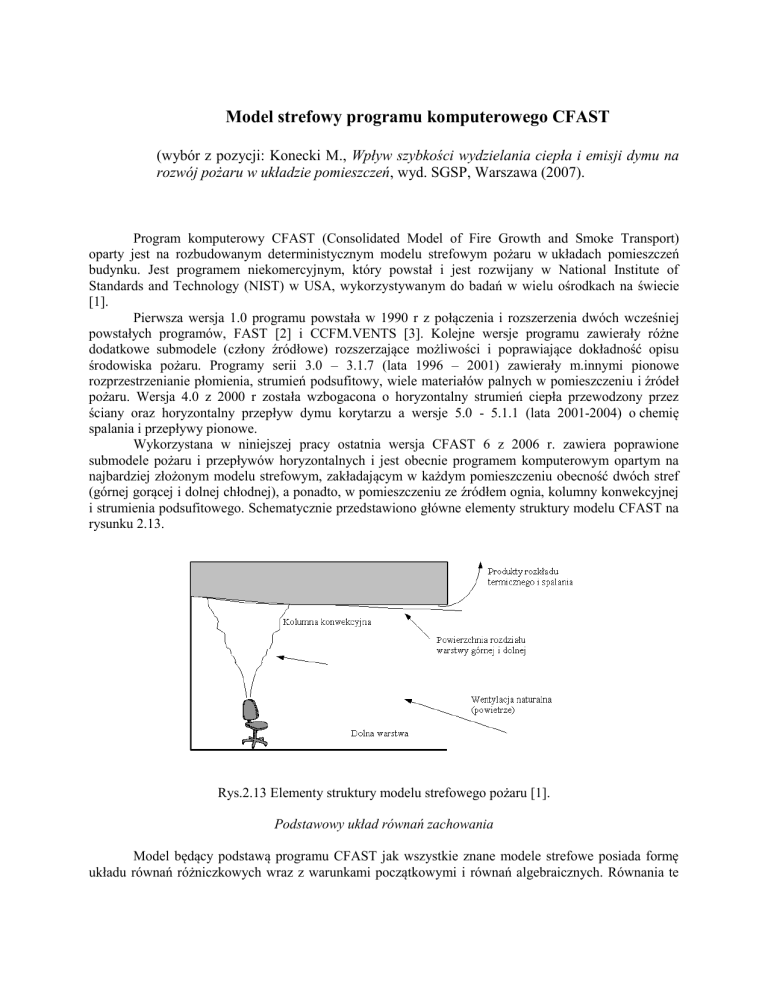
i strumienia podsufitowego. Schematycznie przedstawiono główne elementy struktury modelu CFAST na
rysunku 2.13.
Rys.2.13 Elementy struktury modelu strefowego pożaru [1].
Podstawowy układ równań zachowania
Model będący podstawą programu CFAST jak wszystkie znane modele strefowe posiada formę
układu równań różniczkowych wraz z warunkami początkowymi i równań algebraicznych. Równania te
wyprowadzane z równań zachowania masy, energii uzupełnione są prawem gazu doskonałego z
definicjami gęstości, energii wewnętrznej i formułowane dla każdej strefy lub objętości kontrolnej.
Układ równań różniczkowych zwyczajnych stanowią zależności dla średniego ciśnienia p,
objętości i temperatury górnej warstwy Vg i Tg oraz temperatury dolnej warstwy Td formułowane dla
każdego z rozważanych pomieszczeń:
dp   1 

hd  hg
dt
V
dVg
1
dp 
    1hg  Vg

dt
p 
dt 
dTg
1  
dp 

 hg  c p m g Tg  Vg

dt
c p  gVg 
dt 
dTd
1  
dp 

 hd  c p m d Td  Vd

dt
c p  d Vd 
dt 


(2.37)
(2.38)


(2.39)


(2.40)
gdzie:
γ = cp/cv - stosunek ciepeł właściwych [-], V, Vd, Vg - objętości pomieszczenia, dolnej i górnej warstwy
 d , m g –
[m3], hd , hg – strumienie entalpii i ciepła wpływające do warstwy dolnej i górnej [kJ/s], m
strumienie masy gazów wpływających do warstwy dolnej i górnej [kg/s], ρd, ρg – gęstości dolnej i górnej
warstwy [kg/m3].
Układ równań różniczkowych rozwiązywany jest razem z równaniami algebraicznymi
określającymi energię wewnętrzną i ciśnienie z prawa gazu doskonałego oraz warunkami początkowymi.
Struktura programu CFAST zawiera podstawowe moduły umożliwiające wczytywanie danych,
obliczenia i wydruk w formie graficznej i tekstowej.
Szczegółową dyskusję wszystkich submodeli (członów źródłowych) strefowego modelu pożaru
wraz ze sposobem obliczeń entalpii i strumieni masy oraz procedury numeryczne rozwiązań układów
równań zawarto w pracy [1].
Niżej podano krótki opis najważniejszych z submodeli. Pominięto człony źródłowe takie jak
przepływ w długich korytarzach (o długości powyżej 20 m) czy wentylacja mechaniczna, których nie
stosowano w dalszych rozważaniach.
Źródło pożaru
Zakłada się istnienie wielu niezależnych, nie oddziaływujących wzajemnie stref spalania
w jednym lub w wielu pomieszczeniach.
Spalanie modelowane jest jako kontrolowane przez materiał palny (pożar 1) (w obecności
nieograniczonego dostępu tlenu) lub jako kontrolowane przez wentylację (pożar 2) (ograniczony dostęp
tlenu związany głównie z wielkością otworu wentylacyjnego). W przypadku nieograniczonego dostępu
tlenu Q jest określone jako iloczyn masowej szybkości spalania i efektywnego ciepła spalania.
W przypadkach obu rodzaju pożarów szybkość wydzielania ciepła Q jest opisana zależnością:
 f  c p Tg  T m
f
Q  hs m
gdzie:
(2.41)
hs - ciepło spalania materiału [kJ/kg], m f - masowa szybkość spalania materiału [kg/s], cp - ciepło
właściwe pod stałym ciśnieniem [kJ/kgK], Tg , T - temperatura górnej warstwy i temperatura otoczenia
[K].
 f jest równa szybkości rozkładu
W przypadku pożaru kontrolowanego przez materiał, m
termicznego materiału palnego. W przypadku pożaru kontrolowanego przez wentylację, szybkość spalania
może być mniejsza od szybkości rozkładu termicznego.
Dla pożaru 2, ilości produktów spalania są obliczane z bilansu substancji, w warunkach
ograniczonej ilości tlenu. Przyjęto model spalania polegający na założeniu równowagi chemicznej dla
uproszczonej reakcji spalania wyrażonej w postaci ilorazów masowych produktów do CO2. Skład
chemiczny materiału ulegającemu spalaniu jest charakteryzowany za pomocą jego składu elementarnego i
określony przez udziały masowe tlenu, węgla, wodoru, chloru. Produkty spalania to: tlenek węgla,
ditlenek węgla, dym (węgiel), cyjanowodór, chlorowodór. Założono nieskończoną szybkość reakcji
chemicznych.
Masową szybkość spalania materiału można określić za pomocą masowej szybkości spalania
 c jako:
węgla m
 f   m
c
m
(2.42)
gdzie:
 - stosunek masy materiału palnego do masy elementarnego węgla w tym materiale
  1  H  HCl  HCN  O  

C
C
C
C
f /C
(2.43)
gdzie:
H/C, HCl/C, HCN/C i O/C - stosunki mas składników do masy węgla w materiale [-].
Produkty spalania przedstawiane są w postaci CO2/C, CO/C, H2O/C i S/C. S oznacza cząstki dymu
składające się głównie z węgla.
W przypadku pożaru 1, strumień masy tlenu potrzebny do wytworzenia w reakcjach spalania
danej ilości ciepła w jednostce czasu Q jest określony zależnością:
m o ( potrzebny ) 
h
Q
 m f  s
E
E
(2.44)
gdzie:
E - ciepło wydzielone na jednostkę masy zużytego tlenu równe średnio (dla polimerów) 13,1 [MJ/kg]
 f - masowa szybkość spalania materiału [kg/s], hs
(zasadę zużycia tlenu [4] podano w rozdziale 5.1), m
- ciepło spalania materiału [kJ/kg].
W przypadku pożaru 2, przy niedostatecznej, do całkowitego spalania, ilości tlenu, następuje
zmniejszenie szybkości spalania w stosunku do szybkości rozkładu termicznego.
 o rzeczywisty  jest określony jako:
Rzeczywisty strumień masy tlenu m
 o dostepny , m
 o  potrzebny 
 o rzeczywisty   min m
m
E
m f rzeczywisty   m o rzeczywisty  
hs
gdzie:
 o (dostepny ) obliczany jest z zależności:
dostępny strumień masy tlenu m
(2.45)
(2.46)
 o dostepny   m
 k YO2 C LOL
m
(2.47)
gdzie:
m k - strumień masy powietrza dopływający do obszaru spalania, o stężeniu tlenu 02 [kg/s],
CLOL - współczynnik doświadczalny określający ułamek masowy materiału, który może być spalony przy
udziale dostępnego tlenu [-].
CLOL (0,1) jest funkcją stężenia tlenu i dolnej granicy palności (ang. low flammability limit)
określonej doświadczalnie. W przypadku zmniejszenia stężenia tlenu dopływającego do strefy spalania,
CLOL < 1, co powoduje malenie szybkości wydzielania ciepła Q .
Równanie zachowania masy substratów i produktów w postaci szybkości masowych podano jako:
m f  m O  m f  m f 
hs m f  O 

    m
 m  m  m
 m
 m
  C  CO2 CO s H 2O HCl HCN
E
(2.48)
Niżej podano określenia szybkości masowych (emisji) poszczególnych produktów w odniesieniu
C .
do spalanego węgla, którego strumień masy oznaczono jako m
 HCl 
 HCl 
  m f
m HCl  
  m C  
 C 
 f 
 HCN 
 HCN 
  m f
m HCN  
  m C  
 C 
 f 
m H 2O 
1  H 2O   H 
H
 H  m f

     m C  9     m C  9    
2 H   C 
C
 C  
 CO2 
m CO2  
  m C
 C 
 S 
 CO2   S 
S
  m C  
  m CO2
m s     m C  
  
C 
 C   CO2 
 CO2 
 CO 
 CO2   CO 
 CO 
  m C  
  m CO
m CO  
  
  m C  
CO
 C 
 C   CO2 
2 

(2.49)
(2.50)
(2.51)
(2.52)
(2.53)
(2.54)
Wstawiając powyższe definicje do równania zachowania masy (2.48) otrzymujemy:
CO2

C

hs

E
 1 

O / C   HCl HCN H 


 
   C
C
C

S
CO 
1 


 CO2 CO2 
(2.55)
Biorąc pod uwagę równania (2.52) i (2.55) dostajemy:
m CO2
 hs O / C   HCl HCN H 
1 



  /

E
   C
C
C

 m f 

S
CO 
1 


 CO2 CO2 
Ilorazy mas HCl/C i HCN/C określane są w stosunku do materiału f jako:
(2.56)
 HCl   HCl   H HCl HCN O 
  1  

 

  
C
C
C
C
 C   f  


1 H  O 
 HCl   HCl  
C C
  

  

 C   f    HCl  
 1   f  

 
 HCN   HCN   H HCl O 
  1  
 

  
C
C
C
 C   f  
(2.57)
(2.58)
(2.59)
Podany model źródła pożaru pozwala na obliczanie wydzielania podstawowych produktów
spalania wychodząc z danych doświadczalnych stosunków masowych produktów CO/CO2 i S(cząstki
dymu-głównie C)/CO2, składu materiału palnego wyrażonego stosunkami mas H/C, O/C, HCl/f , HCN/f
oraz znając dolną granicą palności.
Mimo uproszczeń dotyczących postaci równania zachowania masy oraz niezależności od czasu
stosunków H/C i O/C a także pomijania zależności kinetycznych CO/CO2 i S(cząstki dymu)/CO2 od
warunków spalania, model uwzględnia wydzielanie podstawowych produktów w środowisku pożaru.
Reprezentuje obecny poziom chemii pożaru w modelach strefowych.
Kolumna konwekcyjna ognia i strumień podsufitowy
Założono, że siła wyporu generowana wskutek energii cieplnej procesów spalania, powoduje
uformowanie kolumny konwekcyjnej. Masa i entalpia ze źródła ognia są przekazywane w całości do
górnej warstwy. Strefa spalania i kolumna konwekcyjna przekazują energię na drodze promieniowania do
obu warstw, powodując również wzrost temperatury chłodniejszej warstwy dolnej. Efektu tego nie
uwzględnia większość klasycznych modeli strefowych. Zanieczyszczenie produktami spalania i wzrost
temperatury dolnej warstwy, uwzględniono przez dodanie algorytmu, opartego na zależnościach
empirycznych tzw. drzwiowej kolumny konwekcyjnej, występującej w otworze wentylacyjnym
pomieszczenia.
Na rys. 2.14 przedstawiono schemat struktury swobodnej osiowo-symetrycznej kolumny
konwekcyjnej ognia, składającej się ze strefy spalania (płomień) i kolumny konwekcyjnej.
Zgodnie z podstawowym założeniem modeli strefowych, czas przepływu gazów kolumny
konwekcyjnej do stropu pomieszczenia oraz czas przepływu pod stropem do ścian pomieszczenia, są
równe zeru.
Rys.2.14 Ogólna struktura swobodnej osiowosymetrycznej kolumny konwekcyjnej ognia.
Położenie źródła wirtualnego pożaru zo [5]. Zgodnie z Thomasem [6],
z0  1,5 Af gdzie Af oznacza powierzchnię strefy spalania [m2], b – promień
 p - strumień gazów w kolumnie konwekcyjnej
kolumny konwekcyjnej ognia [m], m
ognia [kg/s], Lpl – wysokość płomienia [m].
Zgodnie z teorią Mortona strefa spalania może być podzielona na dwa odrębne obszary. Dolny
obszar stanowi ciągły turbulentny płomień dyfuzyjny. Powyżej w tzw. obszarze płomienia zmiennego
liczba reakcji spalania gwałtownie maleje. W obu obszarach płomienia gazy podlegają dużym siłom
wyporu. Kolumna konwekcyjna stanowi obszar bez reakcji spalania, w którym siły wyporu ulegają
zmniejszeniu (rys. 2.15).
Rys. 2.15 Zmiany względnych wartości parametrów swobodnej kolumny konwekcyjnej ognia w
funkcji jej wysokości z [190]. T0  T0  T gdzie T0 i T oznaczają temperaturę w osi kolumny
konwekcyjnej ognia i temperaturę otoczenia [K], u 0 - prędkość gazów w osi kolumny konwekcyjnej
 p - strumień masy gazów kolumny konwekcyjnej ognia [kg/s].
ognia [m/s], m
Założono kolumnę konwekcyjną ognia McCaffrey’a. McCaffrey [7] określił doświadczalnie
strumień masy dla trzech różnych obszarów kolumny konwekcyjnej ognia (tabela 2.3).
Tabela. 2.3 Parametry kolumny konwekcyjnej ognia McCaffreya.
Obszar kolumny konwekcyjnej
ognia
Strumień masy/
szybkość wydzielania ciepła
Zakres wartości
z / Q 2 / 5
0.566
Płomień ciągły
m p
 z 
 0.011 2 / 5 


Q
Q 
 z 
0.03   2 / 5   0.08

Q 
0.909
Płomień zmienny
m p
 z 
 0.026 2 / 5 


Q
Q 
 z 
0.08   2 / 5   0.20

Q 
1.895
Kolumna konwekcyjna
m p
 z 
 0.124 2 / 5 

Q
Q 
 z 
0.20   2 / 5 

Q 
Korelacja powyższa jest rozszerzeniem modelu punktowego źródła kolumny konwekcyjnej ze
współczynnikami liczbowymi otrzymanymi na drodze analizy regresji danych doświadczalnych, dla
każdego z obszarów. Współczynniki te określają ilość wciąganego powietrza do kolumny konwekcyjnej
ognia. Dla obszaru płomienia zmiennego te same dane otrzymał Cetegen i inni.
Główne ograniczenia modelu McCaffreya związane są niepewnością określenia wartości
liczbowych współczynników wciągania powietrza do kolumny konwekcyjnej ognia i drzwiowej kolumny
konwekcyjnej. Dla układów powyżej trzech – czterech pomieszczeń, sumowanie się niepewności
prowadzi do znaczących różnic między teoretycznymi i eksperymentalnymi szybkościami opadania
górnej warstwy [1]. Inne ograniczenie dotyczy nie uwzględnienia strumieni ściennych w pomieszczeniu,
co jest powodem za małych stężeń produktów spalania i temperatury dolnej warstwy.
Wartości temperatury i prędkości gazów w kolumnie konwekcyjnej obliczone z równań
Heskestada [5] są mniejsze o 10 % od obliczonych zgodnie z zależnościami McCaffreya.
Porównanie z doświadczeniem wskazuje na to, że powierzchnia rozdziału między
warstwą górną i dolną, opada z prędkością zgodną z danymi doświadczalnymi, chociaż tworzy się za
szybko. Autorzy programu CFAST tłumaczą to tym, że strumień powietrza wciąganego do kolumny
konwekcyjnej i chłodzącego ją, nie może być większy od strumienia, przy którym temperatura górnej
warstwy byłaby większa od temperatury kolumny konwekcyjnej. Oznacza to zalożenie braku penetracji
górnej warstwy przez kolumnę konwekcyjną na początku pożaru, co przy szybkim wzroście wydzielanej
mocy może nie być spełnione, wskutek szybkiego wzrostu wysokości płomienia.
Inną przyczyną różnic między doświadczeniem i modelem, jest zwłoka czasowa związana
z przepływami produktów rozkładu termicznego i spalania w kolumnie konwekcyjnej oraz w strumieniu
podsufitowym, co zostało uwzględnione jako modyfikacja modeli strefowych (rozdział 3).
W modelu strefowym programu CFAST, założono pojawienie się strumienia podsufitowego
gazów pożarowych, po zderzeniu kolumny konwekcyjnej ze stropem pomieszczenia.
Przepływy przez otwory wentylacyjne
Strumienie masy są dominującymi członami w równaniach zachowania z powodu wymiany
największych ilości entalpii. W opisie ograniczono się do przepływów poziomych. Przepływy przez
otwory wentylacyjne pomieszczenia są określone różnicami ciśnień, między wnętrzem pomieszczenia a
ośrodkiem zewnętrznym. Równanie zachowania pędu dla powierzchni granicznych warstw (stref) nie jest
rozwiązywane bezpośrednio. W miejsce wymiany pędu na granicach warstw, rozważana jest całkowa
postać równania Eulera – rozwiązanie Bernoulliego, równania prędkości przepływu płynu. Rozwiązanie to
zostało rozszerzone dla przepływów przez otwory rzeczywiste przez wprowadzenie empirycznych
współczynników turbulencji przepływu. Dla otworów prostokątnych wyrażenie na strumień masy można
zapisać jako:
z2
m  W  vdz
(2.60)
z1
gdzie:
W – szerokość otworu wentylacyjnego [m],  - gęstość gazu [kg/m3],  - prędkość gazu o kierunku
prostopadłym do powierzchni otworu [m/s], z – współrzędna pionowa określająca położenie nad
poziomem płaszczyzny podłogi pomieszczenia [m].
Płaszczyzna neutralna (równych ciśnień) określa granice całkowania, podobnie jak płaszczyzna
rozdziału warstwy górnej i dolnej, próg (drzwi) i górna krawędź otworu. Zakłada się jedną strefę
neutralną. Dany strumień masy produktów rozkładu termicznego i spalania lub powietrza, jest obliczany z
równania (2.60) przez całkowanie w odpowiednich granicach (rys.2.16). Można go zapisać jako:
 Pg  xy  Pd 
1
m i o  Cd 8  Aoi 

3
x y


(2.61)
gdzie:
Cd - współczynnik turbulencji przepływu [-],  - gęstość gazu wewnątrz pomieszczeniu ze źródłem
pożaru [kg/m3], x  Pg
1/ 2
, y  Pd
1/ 2
gdzie: Pg i Pd - różnice ciśnień na poziomie górnej i dolnej
granicy danego obszaru (części otworu wentylacyjnego) o powierzchni Aoi .
Zjawisko mieszania występujące w otworach jest analogiczne do wciągania powietrza do
kolumny konwekcyjnej. Gdy gorące gazy z jednego pomieszczenia opuszczają je i przepływają do
przyległego pomieszczenia przez otwór, strumień gazów w otworze jest analogiczny do normalnej
kolumny konwekcyjnej. Ten typ mieszania występuje dla strumienia masy m 13  0 jak pokazano na
rysunku (2.16).
Rys. 2.16 Założony możliwy układ przepływów przez otwór wentylacyjny między pomieszczeniami [1].
Po lewej stronie pomieszczenie ze źródłem ognia.
Aby obliczyć strumień powietrza wciąganego m 43 , przyjęto kolumnę konwekcyjną
z wirtualnym źródłem punktowym opisanym przez Cetegena [173]. To punktowe źródło wirtualne
wybrano tak, aby przepływ w otworze drzwiowym odpowiadał kolumnie konwekcyjnej o ekwiwalentnym
źródle cieplnym z szybkością wydzielania ciepła daną wzorem:
 13
Q ek  c p (T1  T4 )m
(2.62)
gdzie:
Q ek - szybkość wydzielania ciepła z ekwiwalentnego źródła ciepła [kW], c p - ciepło właściwe przy stałym
średnim ciśnieniu w pomieszczeniu ze źródłem ognia[kJ/kgK], T1 - temperatura górnej warstwy w
pomieszczeniu ze źródłem ognia [K], T4 - temperatura dolnej warstwy w pomieszczeniu przyległym [K],
m 13 - strumień masy produktów rozkładu termicznego i spalania przepływający z pomieszczenia ze
źródłem ognia do pomieszczenia przyległego przez otwór wentylacyjny [kg/s].
Założenie źródła wirtualnego oznacza, że strumień entalpii z punktowego wirtualnego źródła
powinien być równy rzeczywistemu strumieniowi entalpii w strumieniu drzwiowym w punkcie wyjścia z
otworu. Strumień powietrza wciąganego jest obliczany tak samo jak dla kolumny konwekcyjnej. Z innym
 42 powoduje powstanie
rodzajem mieszania mamy do czynienia gdy strumień chłodnego powietrza m
 12 . Formuje się przepływ będący typem kolumny
strumienia pochodzącego z górnej warstwy m
konwekcyjnej inwersyjnej powodującej zanieczyszczanie dolnej warstwy powietrza. Przepływ ścinający
powoduje powstanie wirów przekazywanych do dolnej warstwy. Rzeczywista ilość masy i energii
transferowane nie są zwykle duże lecz stanowią zauważalny efekt. Nawet niewielkie ilości cząstek sadzy
będą absorbować strumień promieniowania podwyższając temperaturę dolnej warstwy, która przestaje być
diatermiczna.
Efekt mieszania zwiększa się wraz ze wzrostem różnic gęstości obu warstw. Założono, że suma
strumieni m 12  m 42 zachowuje się jak odwrócona kolumna drzwiowa m 13  m 43 .
Wymiana ciepła
Wymiana ciepła obejmuje wymianę przez promieniowanie między strefami spalania, warstwami
gazów i powierzchniami ścian, stropów, podłóg jak i konwekcyjną wymianę ciepła wewnątrz i na
zewnątrz pomieszczeń a także przewodzenie ciepła przez przegrody budowlane.
Wymiana ciepła przez promieniowanie
Program dokonuje obliczeń strumienia promieniowania netto emitowanego przez każdą
powierzchnię w pomieszczeniu, energii absorbowanej przez każdą warstwę gazową, a także jej
temperaturę i absorbcyjność.
Otrzymane strumienie promieniowania wraz ze strumieniami konwekcyjnymi są dalej użyte jako
warunek początkowy problemu wymiany ciepła przez przewodzenie w celu obliczeń temperatur ściany.
Energia zwrócona nie jest modelowana a straty promieniowania przez otwory wentylacyjne są
zaniedbywane.
Wykorzystany w programie model wymiany ciepła przez promieniowanie Siegela i Howella [8]
zakłada podział wewnętrznych powierzchni pomieszczenia na N małych elementów o temperaturze
jednorodnej Tk (k = 1 ... N), a objętości pomieszczenia na dwie strefy – górną gorącą i dolną chłodną.
Ośrodek gazowy częściowo absorbuje i emituje promieniowanie cieplne.
Rys.2.17 Wymiana ciepła przez promieniowanie w modelu strefowym pożaru [1].
Wymiana ciepła przez promieniowanie na „k”-tym elemencie powierzchni pokazano
schematycznie na rys. 2.17. Zasada zachowania energii pozwala na obliczenie strumienia netto q k
z zależności:
''
Ak  k    Tk4  (1   k )qkin  qkin  Ak qk''
(k = 1, ..., N)
(2.63)
gdzie:
Ak - powierzchnia „k”-ta [m2],  k - współczynnik emisyjności „k”-tej powierzchni [-],  - stała Stefana –
Boltzmana [5.67 x 10-8 W/m2K4], Tk - temperatura „k”-tej powierzchni [K], q kin - strumień
promieniowania padający na powierzchnię „k”-tą [W], q k - gęstość strumienia promieniowania netto,
emitowanego przez powierzchnię „k”-tą [W/m2].
Z równania (2.63), przy uwzględnieniu zasady wzajemności współczynników konfiguracji
Ak Fk  j = A j F j k otrzymujemy równanie:
q k''
k
N


j 1
1 j
j
q 'j' Fk  j   j k  Tk4 
N
T j4 Fk  j  jk  Akk
c
(2.64)
j 1
gdzie:
qk'' , qj - gęstości strumieni promieniowania netto, emitowane przez powierzchnię „k”-tą i „j”-tą
[W/m2], εk , εj - współczynniki emisyjności „k”-tej i „j”-tej powierzchni [-], Fk  j - współczynnik
konfiguracji między powierzchniami „k” i „j” [-],  j k - współczynnik transmisji miedzy ww.
powierzchniami [-], ck - człon reprezentujący strumień ciepła od warstw gazowych i źródła ognia [W].
Równanie (2.64) jest tzw. równaniem promieniowania netto. Dla najczęściej stosowanego
przypadku N = 2, z równania (2.64) otrzymuje się układ dwóch równań, z których oblicza się numeryczne
strumienie promieniowania netto dla każdej powierzchni jako funkcje temperatury powierzchni i gazu
oraz strumienie absorbowane przez warstwy gazu.
Wymiana ciepła przez konwekcję
Wymiana ciepła przez konwekcję polega na wymianie entalpii w warstwie przyściennej, której
grubość jest określona przez różnicę temperatury między gazem i ścianą lub ogrzewanym obiektem.
Konwekcyjny strumień ciepła q c można zapisać jako:
q c  hc (Tg  Tw ) Aw
(2.65)
gdzie:
hc - współczynnik przejmowania ciepła [W/m2K], Tg i Tw - temperatury gazu i ściany [K], Aw - pole
powierzchni ściany lub obiektu będącego w kontakcie z gorącym gazem [m2].
Przy założeniu konwekcji naturalnej współczynnik hc jest określony zależnością:
1
k
hc  Co (Gr Pr) 3
L
(2.66)
gdzie:
k – współczynnik przewodnictwa cieplnego powietrza określony dla średniej temperatury gazu i ściany
[W/mK], Gr - liczba Grashofa [-], Pr - liczba Prandtla, której wartość przyjęto jako stałą równą 0,72 [-], L
– długość charakterystyczna ≈ (Aw)1/2, g – przyspieszenie ziemskie [m/s2], Co - współczynnik zależny od
orientacji powierzchni [-].
Wartości współczynnika Co określone są jedynie dla turbulentnej warstwy przyściennej. Powoduje
to, że otrzymuje się za duże wartości q c w pomieszczeniach odległych od pomieszczenia ze źródłem
pożaru, gdzie mogą dominować laminarne przepływy fazy gazowej.
Ogrzewanie przez konwekcję generuje strumień ciepła z warstwy gazu do powierzchni ściany,
który stanowi warunek brzegowy do obliczeń przewodzenia przez ścianę. Podobny warunek brzegowy
musi być zastosowany do zewnętrznej strony ściany.
Wymiana ciepła przez przewodzenie
Zakłada się, że strumienie promieniowania i konwekcji od górnej gorącej warstwy powodują
powstanie gradientu temperatury i jednowymiarowe przewodzenie energii w kierunku prostopadłym do
powierzchni stropu i ścian. Rozwiązanie problemu przewodzenia ciepła pozwala na określenie
temperatury powierzchni ścian.
Równanie, nieustalonego jednowymiarowego przewodzenia cieplnego jest określone jako:
T/t = (ks/scs) 2T/x
(2.67)
gdzie:
ks - współczynnik przewodnictwa cieplnego ściany [W/mK], s – gęstość ściany [kg/m3], cs - ciepło
właściwe ściany [J/kgK].
Dla większości materiałów przyjęto niezależność ks, s oraz cs od temperatury co powoduje, że
powyższe równanie jest liniowe. W przypadku niektórych materiałów takich jak gips i betony komórkowe
ks zależy od temperatury i przybliżenie to przestaje obowiązywać. Uwzględnienie tych zmian (kilkukrotny
wzrost ks) powoduje niewielkie obniżenie temperatury górnej warstwy (2 – 3°C) w pomieszczeniach o
objętościach rzędu 50 m3 i nie ma wpływu na położenie górnej warstwy. Rozwiązanie jednowymiarowego
równania przewodzenia ciepła jest dokonywane przy użyciu metody różnic skończonych lub metody
elementów skończonych.
Walidacja programu komputerowego CFAST
Rozszerzenie modelu programu CAFST, w stosunku do innych modeli strefowych, polega na
uwzględnieniu większej niż jedna niezależnych stref spalania, zmian ciśnienia w pomieszczeniu ze
źródłem pożaru i w pozostałych pomieszczeniach, mieszania się gazów warstw górnych i dolnych
w pomieszczeniach (strumienie drzwiowe) co prowadzi do zmiany temperatury i stężenia gazów
toksycznych w dolnej warstwie, własności termofizycznych materiałów wielowarstwowych ścian, sufitów
i podłóg pomieszczeń oraz zmiany szybkości wydzielania ciepła w czasie symulacji pożaru, związane ze
zmianą strumienia tlenu dopływającego do strefy spalania. Wprowadzono również model horyzontalnego
przepływu dymu w długich korytarzach budynku.
Mimo stosunkowo dobrej zgodności wartości obliczonych z danymi eksperymentalnymi, model
strefowy CFAST posiada ograniczenia, a także braki wynikające z nie uwzględnienia różnych zjawisk w
środowisku pożaru lub potraktowanie ich w sposób nadmiernie uproszczony co w sposób oczywisty ma
wpływ na wyniki obliczeń .
Nie uwzględniono przepływu dymu wzdłuż ścian pomieszczeń co prowadzi do zaniżenia stężeń
gazów w dolnych warstwach jak i czasów przepływu gazów w kolumnie konwekcyjnej i w strumieniu
podsufitowym.
Model nie opisuje złożonych przepływów gazów w budynkach o złożonej geometrii. Do opisu
środowiska pożaru w ciągach pionowych budynku (klatki schodowe, szyby wind i inne) zamiast modelu
dwustrefowego stosuje się uproszczony model jednostrefowy.
Ograniczenia dotyczą również wymiarów pomieszczeń określonych stosunkiem
długość/szerokość i wysokość pomieszczenia ze źródłem ognia, co wynika z wielkości kolumny
konwekcyjnej. Jeżeli stosunek długość/szerokość pomieszczenia jest większy od 10, stosowany jest
osobny algorytm przepływu dymu w korytarzu budynku.
W celu walidacji programu CFAST, w szeregu pracach, porównano wyniki obliczeń z danymi
doświadczalnymi pożarów w skali rzeczywiste co przedstawiono w publikacji [1]. Niżej przytoczono
wyniki walidacji otrzymane przez wybranych autorów, reprezentatywne dla wszystkich
przeprowadzonych do tej pory prób doświadczalnych. Na rysunkach 2.18 i 2.19 podano charakterystyczne
wyniki obliczeń i pomiarów położenia i temperatury górnej warstwy otrzymane w pracy [9]. Pożary
doświadczalne powadzono w pomieszczeniu o wymiarach 3,3 m x 3,4 m x 3,05 m (wysokość) i z
otworami wentylacyjnymi. Ulegały spalaniu stosy drewna lub płyty z pianki poliuretanowej elastycznej.
Stosowano zmienną wentylację.
Na rysunku 2.18 podano wyniki położenia górnej warstwy w czasie. Dane eksperymentalne
otrzymano dla pożaru pianki poliuretanowej o maksymalnej szybkości wydzielania ciepła 1100 kW.
Obserwowano szybsze zmniejszanie się obliczeniowego położenia górnej warstwy w czasie
w stosunku do wyników eksperymentalnych na początku trwania pożaru, co jest charakterystyczne dla
pozostałych pożarów doswiadczalnych.
4
3,5
Dane doświadczalne
Położenie górnej warstwy [m]
3
Program CFAST
2,5
2
1,5
1
0,5
0
0
50
100
150
200
250
300
350
400
450
Czas [s]
Rys. 2.18 Porównanie wyników obliczeń i pomiarów położenia górnej warstwy [9]. Pożar pianki
poliuretanowej. Szybsze zmniejszanie się obliczeniowego położenia górnej warstwy w czasie w stosunku
do wyników eksperymentalnych na początku trwania pożaru.
Na rysunku 2.19 przedstawiono zależność temperatury górnej warstwy od czasu, określoną dla
eksperymentu podanego wyżej. Pokazany przebieg danych doświadczalnych w porównaniu
z obliczeniowymi jest charakterystyczny dla innych testów. Średnie nadwyżki temperatury obliczeniowej
w stosunku do eksperymentalnej nie przekraczały 50°C.
400
350
Dane doświadczalne
Program CFAST
Temperatura górnej warstwy [°C]
300
250
200
150
100
50
0
0
50
100
150
200
250
300
350
400
450
Czas [s]
Rys. 2.19 Porównanie wyników obliczeń i pomiarów temperatury górnej warstwy [9]. Pożar
pianki poliuretanowej.
Na rysunku 2.20 pokazano przykładowe wyniki obliczeń przy użyciu programu CFAST
i porównanie z danymi eksperymentalnymi otrzymanymi dla pożaru materaca z pianki poliuratanowej o
szybkości wydzielania ciepła zapisanej jako funkcja czasu Q = 0,019 t2, w pomieszczeniu ze źródłem
ognia o powierzchni 26 m2 i wysokości 2,7 m.
3
Dane doświadczalne
Program CFAST
Położenie górnej warstway [m]
2,5
2
1,5
1
0,5
0
0
50
100
150
Czas [s]
200
250
Rys. 2.20 Zwłoka czasowa spowodowana nie uwzględnieniem przez model programu komputerowego
CFAST czasu przepływu w kolumnie konwekcyjnej i w strumieniu podsufitowym [10]. Pożar pianki
poliuretanowej. Szybsze zmniejszanie się obliczeniowego położenia górnej warstwy w czasie w stosunku
do wyników eksperymentalnych na początku trwania pożaru.
W tabeli 2.4 przedstawiono wyniki walidacji programu CFAST na podstawie danych z prac [10]
podanych na rysunkach 2.18 – 2.20. Funkcje  s   s (t ) i  m   m (t ) oraz z s  z s t  i
z m  z m t  dla scenariuszy opisanych w pracach [10], przybliżano wielomianami różnych stopni, na
drodze analizy regresji nieliniowej. Względne niepewności obliczano ze wzorów 2.35 i 2.36.
Tabela 2.4 Walidacja komputerowego programu pożarowego CFAST.
Względna niepewność temperatury
górnej warstwy
[%]
Względna niepewność położenia
górnej warstwy
[%]
Rodzaj testu
Pomieszczenie o objętości 34,2 m3.
Pożar pianki poliuretanowej [192]
Pomieszczenie o objętości 70,2 m3.
Pożar pianki poliuretanowej [195]
* - podano w publikacji [195].
E
E max
E
E max
20
35
25
45
19*
37
19*
44
Próby testowe przeprowadzone w różnych układach pomieszczeń budynku dla różnych szybkości
wydzielania ciepła [1], w tym przytoczone w niniejszej pracy, wskazują na różnice wartości
doświadczalnych i obliczeniowych, osiągające średnie wartości 25 %.
W publikacji opisującej 6 wersję programu CFAST [1], autorzy programu przedstawili zbiorcze
zestawienie walidacji CFAST przy użyciu różnych testów pożarowych przeprowadzonych przez różnych
badaczy.Wyniki walidacji dotyczące temperatury i położenia górnej warstwy przedstawiono w tabelach
2.5 i 2.6. Obliczono wartości parametrów takich jak: temperatura górnej i dolnej warstwy, położenie
dolnej krawędzi górnej warstwy, stężenia gazów i inne. Próby testowe przeprowadzono w różnych
układach pomieszczeń od pojedynczego o objętości 21 m3 do 7 piętrowego budynku o obj. 140 000 m3.
Szybkości wydzielania ciepła (maksymalne wartości) zmieniano w granicach od 100 kW (palnik gazowy)
do 7 MW (pożar mebla i ściany).
Tabela 2.5 Walidacja CFAST. Porównanie eksperymentalnych i obliczeniowych wartości
temperatury górnej warstwy. Dla pojedynczego pomieszczenia średnie względne
niepewności E dotyczą maksymalnej temperatury obliczeniowej górnej warstwy.
W pozostałych przypadkach układów pomieszczeń odnoszą się do ustalonej wartości
temperatury. Dane doświadczalne (w nawiasach) - średnie wyniki pomiarów w pięciu
testach pożarowych [1].
Rodzaj testu w pełnej skali
Pojedyncze pomieszczenie,
  2,9 MW
pożar mebli. Q
max
(Test 1 i 6)
Pojedyncze pomieszczenie,
pożar materiałów
wykończeniowych ściennych
(Test 1 i 2)
Q max  7 MW
Układ trzech pomieszczeń z
korytarzem, palnik gazowy
Wartość
maksymalna
temperatury
C
Czas osiągnięcia
temperatury
maksymalnej
s
Wartość
ustalona
temperatury
C
500 (510)
450 (510)
510 (520)
510 (520)
710 (230)
Czas
osiągnięcia
temperatury
100C
s
290 (250)
290 (250)
330 (260)
330 (260)
100 (140)
790 (780)
920 (780)
590 (660)
900 (660)
750 (620)
810 (1190)
520 (470)
100 (80)
-
-
-
-
-
Q max  1MW
Budynek wielopiętrowy
-
18
5
Q max  100kW
Układ czterech pomieszczeń z
korytarzem, palniki gazowe
E
%
-
-
Q max = 3MW
1* - 100 (120)
2 - 830 (n. o.)
3 - n.o.
1 - 230 (215)
2 - 75 (90)
3 - 45 (50)
1 - 195 (195)
2 - n.o. (240)
3 - n.o.
4 - n.o.
390 (180)
210 (390)
n.o.
1 - 240 (370)
2 - 70 (90)
3 - 55 (35)
4 - 40 (35)
270 (340)
110 (110)
15 (15)
26
22
33
n.o. – nie osiągnięto w eksperymencie,* - numer pomieszczenia.
Najlepszą zgodność teorii z doświadczeniem otrzymuje się dla układów do 3 – 4 pomieszczeń o
objętości 40-60 m3 każde lub układu pomieszczenie – korytarz. Średnia względna niepewność określenia
parametrów pożaru wynosi 25 % [1].
Wartości obliczeniowe temperatury i położenia górnej warstwy przewidywane przez CFAST są
nieco wyższe od wartości eksperymentalnych. Wyższe położenie warstwy górnej powoduje, że ma ona
mniejszą objętość, co dla danej entalpii przekazywanej do mniejszej objętości daje wynik w postaci
wyższej temperatury.
W układach 3 - 4 pomieszczeń oraz w większych przestrzeniach budynku, w fazie rozwoju
pożaru, w odróżnieniu od pomieszczenia ze źródłem ognia, osiągane są stany ustalone temperatury, które
dobrze charakteryzują różnice między wartościami obliczeniowymi i doświadczalnymi.
Obliczone wartości strumieni masy są zwykle mniejsze, od doświadczalnych co jest
spowodowane niedoskonałością teorii kolumn konwekcyjnych w otworach wentylacyjnych. Stężenia CO2
(jak i CO) są mniejsze od określonych eksperymentalnie co jest związane prawdopodobnie z założeniem
uproszczonego submodelu szybkości spalania jako funkcji stężenia tlenu w pomieszczeniu.
Tabela 2.6 Walidacja CFAST. Porównanie eksperymentalnych i obliczeniowych wartości położenia
górnej warstwy. Niepewności położenia górnej warstwy E obliczone przy użyciu
CFAST dotyczą pojedynczego pomieszczenia. W pozostałych przypadkach układów
pomieszczeń odnoszą się do ustalonej wartości położenia górnej warstwy. Dane
doświadczalne (w nawiasach) – średnie wyniki pomiarów w pięciu testach pożarowych
[1].
Rodzaj testu w pełnej skali
Pojedyncze pomieszczenie
Pojedyncze pomieszczenie –
pożar materiałów
wykończeniowych ściennych
Układ trzech pomieszczeń z
korytarzem.
Układ czterech pomieszczeń z
korytarzem.
Budynek wielopiętrowy
Wartość
minimalna
położenia
m
Czas osiągnięcia
położenia
minimalnego
s
0,8 (0,3)
0,8 (0,3)
0,8 (0,5)
0,9 (0,5)
0,2 (0,7)
420 (480)
450 (480)
480 (510)
460 (510)
710 (220)
0,1 (0,6)
-
500 (410)
-
Czas
osiągnięcia
położenia
1m
s
400 (390)
380 (390)
420 (430)
430 (430)
120 (210)
Wartość
ustalona
położenia
m
80 (280)
1* - 360 (n.o)
2 - 1210 (n.o)
3 - 90 (n.o)
n.o.
1 - 1,0 (1,7)
2 - 1,2 (1,6)
3 - 0,9 (1,3)
1 - 0,7 (1,7)
2 - 1,0 (1,8)
3 - 1,0 (1,7)
4 - 0,7 (1,7)
1 - 0,8 (1,5)
2 - 0,9 (1,4)
3 - 0,8 (1,2)
4 - 0,6 (1,2)
0,3 (0,6)
0,8 (0,8)
1,8 (0,9)
E
%
18
20
-
-
-
-
-
-
n.o.
n.o.
28
40
33
n.o. – nie osiągnięto w eksperymencie, * - numer pomieszczenia.
Poziom położenia górnej warstwy zależy głównie od strumienia powietrza, wciąganego pod
wpływem parcia zewnątrzego, do kolumny konwekcyjnej ognia, który jest określony za pomocą modelu
McCaffreya dla kolumn o przekrojach kołowych, w stosunkowo małych pomieszczeniach. W przypadku
dużych szybkości wydzielania ciepła i sięgania płomienia do stropu pomieszczenia (ma to miejsce w
przypadku spalania materiałów wykończeniowych ściennych w pojedynczym pomieszczeniu) lub dla
małych Q w dużych przestrzeniach budynku, korelacje McCaffreya mogą nie być spełnione. Tłumaczy to
większe niepewności otrzymane w przypadku pożaru materiałów wykończeniowych w pomieszczeniu i
dla budynku wielopiętrowego.
W celu określenia wpływu zmian wartości różnych parametrów wprowadzanych jako dane
wejściowe na wyniki obliczeń, przeprowadziłem parametryczną analizę wrażliwości programu
komputerowego CFAST. Wyniki obliczeń podano tabeli 2.7.
Tabela 2.7 Analiza wrażliwości temperatury górnej i dolnej warstwy oraz położenia górnej warstwy na
zmianę wartości danych wejściowych dla układu dwóch pomieszczeń.
Badany parametr
Zmiana temperatury
górnej warstwy
Zmiana temperatury
dolnej warstwy
Td (%)
Tg (%)
Zmiana położenia górnej
warstwy
z (%)
Pom.1
Pom.2
Pom.1
Pom.2
Pom.1
Pom.2
Szybkość wydzielania ciepła
6,8
6,4
3,9
1,2
0,0
-0,01
Udział promieniowania ( χ )
-1,5
-1,5
2,8
0,4
0,7
0,0
Współczynnik przewodnictwa
cieplnego ścian ks
Parametr emisji dymu f
- 0,7
0,02
0,2
0,0
0,0
0,0
-0,8
-2,1
0,6
0,0
0,0
0,0
Szerokość drzwi
-2,9
-1,6
-2,6
-1,6
2,4
2,2
Wysokość drzwi
-8,9
-6,2
-4,8
-1,3
7,9
8,7
Przedstawione w tabeli 2.7 wyniki obliczeń wykonano dla układu dwóch pomieszczeń (Pom. 1 i
Pom. 2) o wymiarach 3,66 m długości, 2,44 m szerokości, 2,44 m wysokości każde, połączonych ze sobą
otwartymi drzwiami o szerokości 1 m i wysokości 2 m. Pomieszczenie 2 posiadało drzwi wyjściowe
o wymiarach 1 m x 2 m. Źródło spalania o ustalonej mocy (100 kW) znajduje się w pomieszczeniu 1.
Każda ściana zbudowana była z płyt gipsowych o grubości 0,016 m i bezwładności cieplnej
5,8·105 W2s/m4K2.
Wartość każdego z parametrów (dane wejściowe do modelu) poddawano niewielkim zmianom
(przy stałych wartościach pozostałych) i badano zmiany wartości parametrów obliczanych (dane
wyjściowe). Wartości szybkości wydzielania ciepła (100 kW), udziału promieniowania
(wypromieniowywanej części energii ze strefy spalania – χ = 0,3), współczynnika przewodnictwa
cieplnego ścian ks = 0,14 W/mK, szerokości drzwi (1 m) i wysokości drzwi (2 m) zwiększano o 10 %.
Zmiana szybkości wydzielania ciepła ma największy wpływ na temperaturę górnej warstwy oraz
warstwy dolnej. Obserwuje się brak wpływu zmiany Q na położenie warstwy gorącej. Wzrost udziału
promieniowania w bilansie cieplnym pomieszczenia 1, jak pokazano wyżej, wywiera znaczący wpływ na
wzrost temperatury dolnej „chłodnej” warstwy, zmniejszając strumień entalpii przenoszonej
konwekcyjnie co w konsekwencji powoduje zmniejszenie temperatury warstwy górnej. Wzrost
współczynnika przewodnictwa cieplnego ścian pomieszczenia 1 powoduje niewielkie obniżenie
temperatury warstwy górnej. Wyniki analizy potwierdzają wpływ wzrostu stężenia cząstek dymu wskutek
wzrostu generacji dymu z materiału, na zwiększenie się emisyjności dymu. Powoduje to wzrost energii
traconej i w konsekwencji obniżenie temperatury warstwy górnej.
Zwiększenie wysokości drzwi ma wpływ na wzrost położenia warstwy górnej. Powoduje
największe obniżenie temperatury warstwy górnej w pomieszczeniu 1.
Na rysunku 2.21 pokazano wyniki określenia wrażliwości temperatury na zmianę szybkości
wydzielania ciepła w K/kW w podanym wyżej układzie modelowym pomieszczeń.
Rys. 2.21
Wpływ zmiany szybkości wydzielania ciepła na zmiany temperatury górnej i dolnej warstwy
w funkcji Q w układzie dwóch pomieszczeń [opracowanie własne].
Przedstawione obliczenia są powtórzeniem obliczeń wykonanych przez autorów programu przy
założeniu rozwoju pożaru w układzie czterech pomieszczeń [167]. Wrażliwość opisaną jako T / Q
określono, obliczając temperaturę górnej warstwy dla każdego Q oraz Q  0,1Q w zakresie szybkości
wydzielania ciepła od 10 kW do 200 kW (co 10 kW), od 200 kW do 1000 kW (co 100 kW) oraz od 1000
kW do 3500 kW (co 500 kW). Otrzymano przebiegi funkcji ( rys.2.21) bardzo zbliżone do wyników
zawartych w pracy [167]. Z przeprowadzonych symulacji przy użyciu programu komputerowego CFAST
wynika, że w zakresie stosunkowo małych wartości Q do ok. 200 kW (początek fazy pożaru) wrażliwość
górnej warstwy w pomieszczeniu ze źródłem ognia wynosi od 1 do 0,6 K/kW. Powyżej 500 kW
wrażliwość maleje do wartości 0,2 – 0,3 K/kW. Temperatura dolnej warstwy jest mniej wrażliwa na
zmiany szybkości wydzielania ciepła i maleje od wartości 0,2 do 0,1 gdy Q osiąga 1 MW. Powyżej tej
wartości maleje nieznacznie.