przyblizenie elektronow swobodnych, prawie swobodnych i silnie

GAZ ELEKTRONÓW
Ó SWOBODNYCH
POWYŻEJ ZERA BEZWZGLĘDNEGO.
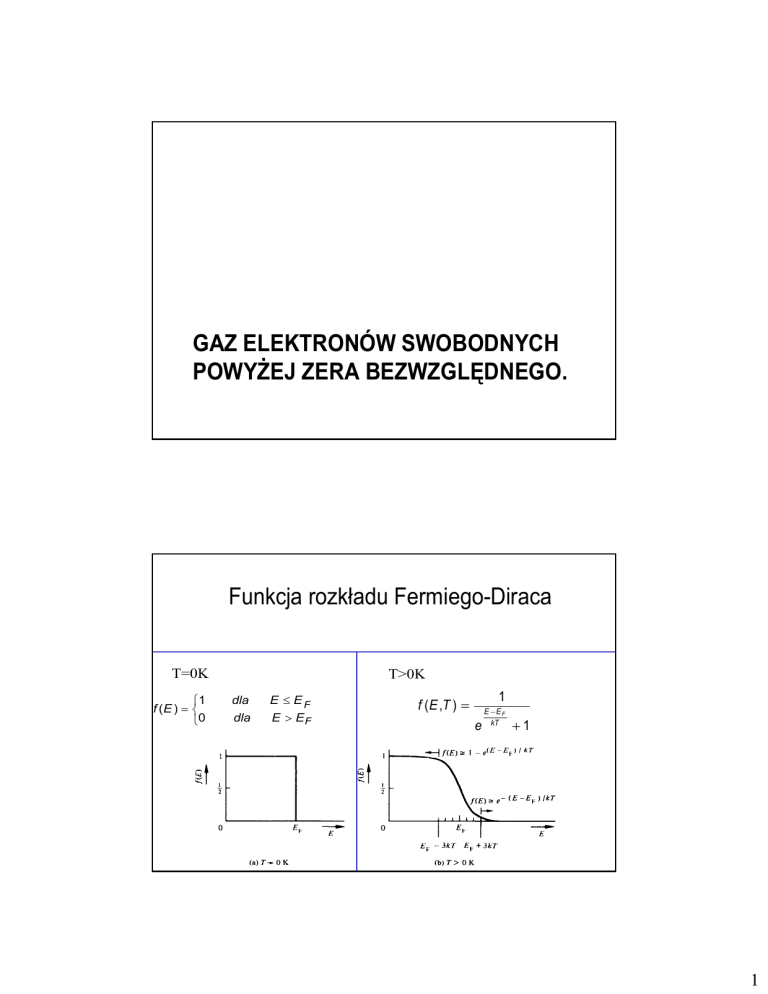
Funkcja rozkładu Fermiego-Diraca
T=0K
⎧1
f (E ) = ⎨
⎩0
T>0K
dla
dla
E ≤ EF
E > EF
1
f ( E ,T ) =
e
E −EF
kT
+1
1
Funkcja rozkładu Fermiego-Diraca
T>0K
FERMI FUNCTION f(E)
EF/kB = 10000 K
0 K
1
0 .8
f (E = EF ) =
0 .6
1
1
=
exp[0] + 1 2
0 .4
3 0 0
0 .2
K
3 0 0 0 K
0
0
4 0 0 0
8 0 0 0
1 2 0 0 0
1 6 0 0 0
E/kB (KELVIN)
f (E = EF + kT ) =
1
≈ 27 %
e +1
1
f (E = EF + 3kT ) =
≈5%
3
e +1
1
f (E = EF + 5kT ) =
≈ 1%
5
e +1
1
Temperatura powoduje zmianę
obsadzenia stanów w przedziale
kilku kT wokół energii Fermiego
Gaz elektronów swobodnych T>0K
• Elektron może przejść do wyższych stanów
energetycznych w temperaturze TT, jeżeli istnieją stany
nieobsadzone. Oznacza to, że tylko niewielka liczba
elektronów w metalu może zostać wzbudzona
(D(EF)kT)
http://www.physicsforidiots.com/condensedmatter2.html
2
Energia Fermiego bardzo słabo zależy od temperatury
⎛
µ = EF ⎜⎜1 −
⎝
2
π 2 ⎛ kT ⎞ ⎞⎟
⎜
⎟
12 ⎜⎝ EF ⎟⎠ ⎟
⎠
Średnia energia elektronu w paśmie przewodnictwa:
Eel =
Eel =
3
EF
5
⎛ 5π 2 ⎛ kT
3
⎜
EF ⎜⎜1 +
5
12 ⎜⎝ EF
⎝
⎞
⎟⎟
⎠
2⎞
⎟
⎟
⎠
Pasmo energetyczne: zespół mało różniących się od siebie poziomów
energetycznych elektronów.
PASMA ENERGETYCZNE
3
Przybliżenie elektronów swobodnych
• Przybliżenie elektronów swobodnych ignoruje sieć
krystaliczną:
– nie uwzględnia periodyczności sieci;
– nie uwzględnia istnienia różnych atomów.
• Nie wyjaśnia istnienia pasm energetycznych, ani różnic
pomiędzy ciałami stałymi.
Przybliżenie elektronów prawie
swobodnych
• W ramach tego przybliżenia zakłada się , że elektron
może sięę poruszać
p
w sieci krystalicznej.Ciało
y
j
stałe jjest
studnią potencjału o modulowanym dnie. Modulacja jest
zgodna z periodycznością sieci krystalicznej.
http://www.globalspec.com/reference/62495/203279/10-2-nearly-free-electron-model-of-solids-andthe-bloch-theorem
4
Dyfrakcja Bragga
• Gdy fala rozchodzi się w periodycznym ośrodku, może ona
ulec odbiciu (dyfrakcji) Bragga.
Bragga Odbicie zachodzi
zachodzi, jeśli
długość fali spełnia warunek: λ = 2dsinθ;
• Jakiemu pędowi elektronu odpowiada ta długość fali?
Notabene: co oznacza k=±π/a?
5
Co oznacza k=±π/a?
Sieć rzeczywista
y
Sieć odwrotna
c
a
2π r
r
a* =
i
a
b
r r
r r
r
r
a = ai , b = aj , c = ak
r
2π r v
2π r
b* =
j , c* =
k
a
a
Co oznacza k=±π/a?
Granice I strefy
Brillouina
6
Przybliżenie elektronów prawie
swobodnych
• Ponieważ dno studni potencjału jest modulowane
periodycznie (stała sieci = a),
a) to elektron o wektorze
falowym k=±π/a musi ulec dyfrakcji Bragga.
• To znaczy, że fali o k=π/a musi towarzyszyć k=-π/a (i
odwrotnie): powstaje fala stojąca. Ściśle mówiąc są
dwie możliwości:
Ψ± = A(sin(ωt − kx ) ± sin(ωt + kx ))
http://usersphys.au.dk/philip/pictures/physi
csfigures/physicsfigures.html
Przybliżenie elektronów prawie
swobodnych
• Możliwość 1: Ψ+ = A(sin(ωt − kx ) + sin(ωt + kx ))
Ψ+ = 2 A(sin(
ωt − kx + ωt + kx
) cos(
ωt − kx − ωt − kx )
2
Ψ+ = 2 A(sin(ωt ) cos(kx )
2
)
• Strzałki: kx=0, π itd.
http://usersphys.au.dk/philip/pictures/physi
csfigures/physicsfigures.html
7
Przybliżenie elektronów prawie
swobodnych
• Możliwość 2: Ψ− = A(sin(ωt − kx ) − sin(ωt + kx ))
Ψ+ = 2 A(sin(
ωt − kx − ωt − kx
2
) cos(
ωt − kx + ωt + kx )
2
)
Ψ+ = −2 A(cos(ωt ) sin(kx )
• Strzałki: kx=1/2 π, 3/2 π itd.
http://usersphys.au.dk/philip/pictures/physi
csfigures/physicsfigures.html
Przybliżenie elektronów prawie
swobodnych
• W zależności od tego gdzie są węzły i strzałki fali
stojącej mamy wyższą i niższą energię elektronu.
stojącej,
elektronu
8
Przybliżenie elektronów prawie
swobodnych
• W zależności od tego gdzie są węzły i strzałki fali
stojącej mamy wyższą i niższą energię elektronu.
stojącej,
elektronu
Przybliżenie elektronów prawie
swobodnych
• Oznacza to, że na granicy strefy Brillouina powstają
pasma energii wzbronionych.
wzbronionych
9
Nie wszystkie elektrony są prawie swobodne
• Tylko elektrony znajdujące się daleko od jądra mogą
być prawie swobodne.
swobodne Elektrony z wewnętrznych
poziomów są zlokalizowane a ich energie różnią się
niewiele od energii w izolowanym atomie.
http://web.utk.edu/~cnattras/Phys250Fall2012/modules/module%204/conduction_in_solids.htm
Przybliżenie elektronów silnie
związanych
• W ramach tego przybliżenia, elektron uważamy za
związany z atomem - nie może swobodnie poruszać się
w krysztale. Energia elektronu w krysztale jest równa
sumie energii potencjalnej, takiej jak w atomie
swobodnym i małego, zaburzenia.
10
Przybliżenie elektronów silnie
związanych
• W tym przybliżeniu "wyobrażamy sobie" jak funkcje
falowe atomów lub jonów oddziałują ze sobą gdy
zbliżamy je do siebie. Np. w cząsteczce wodoru z
dwóch identycznych poziomów atomowych powstają
dwa poziomy energetyczne przesunięte względem
siebie.
Przybliżenie elektronów silnie
związanych
• N atomów w ciele stałym (1023 cm–33) daje N poziomów
energetycznych w paśmie
2 atomy
6 atomów
N atomów
11
Przybliżenie elektronów silnie
związanych
• Zatem: wskutek rozszczepienia atomowych poziomów
energetycznych powstają pasma energetyczne.
Teoria pasmowa
• Oba przybliżenia prowadzą do tego samego wniosku:
stany energetyczne elektronów w ciele stałym tworzą
pasma energetyczne.
• Pasmo energetyczne: zespół mało różniących się od
siebie poziomów energetycznych elektronów.
12
Teoria pasmowa
• PASMOWA TEORIA CIAŁA STAŁEGO, teoria
tłumacząca właściwości elektronowe ciał stałych; opiera
się na założeniu, że podczas powstawania struktury
krystalicznej ciała stałego dozwolone dla elektronów
poziomy energetyczne swobodnych atomów
rozszczepiają się tworząc pasma poziomów blisko
leżących;
Teoria pasmowa
• Poszczególne pasma mogą być od siebie oddzielone
pasmem wzbronionym (przerwą energetyczną);
najwyższe, całkowicie lub częściowo wypełnione
elektronami pasmo jest nazywane pasmem
walencyjnym, a kolejne wyższe, całkowicie lub prawie
całkowicie puste — pasmem przewodnictwa.
13
Teoria pasmowa
• W niecałkowicie zapełnionym paśmie pole
elektryczne może spowodować przeniesienie elektronu
na sąsiedni poziom energetyczny, tj. wywołać przepływ
prądu, w całkowicie zapełnionym paśmie nie może
ono zmieniać pędu elektronu, a więc nie wywołuje
przepływu prądu.
Przykład: krzem
Konfiguracja elektronowa Si
1s22s22p63s23p2
Pasma?
14
Przykład: krzem
masa efektywna
dziury dodatnie
KONSEKWENCJE ISTNIENIA PASM
ENERGETYCZNYCH
15
Masa efektywna
• Przybliżenie masy efektywnej – jest to pewien sposób
uwzględnienia oddziaływania elektronów z siecią
krystaliczną.
– Prędkość grupowa fali, prędkość cząstki:
v=
dω 1 dE
=
dk h dk
– Druga
D
zasada
d dynamiki
d
iki Newtona:
N t
F = ma =
dp
dk
=h
dt
dt
Masa efektywna
– przyspieszenie
a=
a=
ddv 1 ∂ 2E
=
dt h ∂k∂t
a=
1 ∂ 2E dk
h ∂k∂t dk
1 ∂ 2E dk
h ∂k 2 dt
(m *) −1 =
ma = h
dk
dt
1 ∂ 2E
h 2 ∂k 2
16
Masa efektywna
Masa efektywna elektronu w paśmie o danym związku
dyspersyjnym E(k).
m* =
Dla elektronów
swobodnych:
y
h2
d 2E / dk 2
1
1 p2 h2 2
E = mv 2 =
=
k
2
2 m 2m
→ m* = m
Zależność E, v i m od k: rysunki
Masa efektywna
• Masa efektywna zależy od
krzywizny pasma;
• Elektrony na wierzchołku
pasma walencyjnego mają
ujemne masy efektywne;
• W ogólności, m* zależy od
kierunku: jest tensorem;
17
Masa efektywna: z.d.
6
Uzasadnić, w których
pasmach (6 pasm
oznaczonych kolejnymi
numerami) będzie
większa a w których
większa,
mniejsza masa
efektywna.
5
4
3
2
1
Pojęcie dziury
Rozważmy pasmo
walencyjne całkowicie
zapełnione
Całkowity prąd N elektronów w całkowicie wypełnionym paśmie:
N
J = (−q)∑ v i = 0
i
18
Pojęcie dziury
Pasmo walencyjne,
całkowicie zapełnione.
Pokazane są stany
elektronowe jty z wektorem
falowym kj i j’ z przeciwnie
skierowanym wektorem
falowym -kj . Gdy usuniemy
elektron jty wówczas ruch
elektronu j’ nie jest
skompensowany.
Pojęcie dziury
Zatem, całkowity prąd, gdy brakuje jtego elektronu
N
J = (−q)∑ v i − (−q)v j = qv j
i
WYNIK: ŁADUNEK DODATNI PORUSZA SIĘ Z PRĘDKOŚCIĄ vj
19
Pojęcie dziury
Zamiast rozważać dużą liczbę
elektronów w niecałkowicie
wypełnionym paśmie
walencyjnym (cząstek o
ujemnym ładunku i ujemnej
masie efektywnej), rozważamy
małą liczbę dziur (cząstek o
dodatnim ładunku i dodatniej
masie efektywnej).
Poziomy energetyczne w atomie sodu
20
Poziomy energetyczne w hipotetycznej
cząsteczce Nɑ4
Poziomy
energetyczne
czterech elektronów
3s są nieco
g
siebie
względem
przesunięte.
Pasma energetyczne w stałym sodzie
Też pasma,
tylko wąskie
21
STRUKTURY PASMOWE:
PRZYKŁADY
Metale, półprzewodniki, izolatory
a) Metale mają swobodne elektrony i częściowo zapełnione najwyższe
pasmo (lub nakładające się pasma).
22
Metale, półprzewodniki, izolatory
b i c) Półprzewodniki i izolatory mają zapełnione pasmo walencyjne i puste
pasmo przewodnictwa rozdzielone przerwą energetyczną
Metale, półprzewodniki, izolatory
Pół t l mają
Półmetale
j najwyższe
j ż
pasmo zapełnione.
ł i
T pasmo nakłada
To
kł d się
i na
następne, wyższe pasmo tak, że koncentracja swobodnych elektronów jest
mała, ale różna od zera również w 0K. Jednocześnie obecne są dziury.
23
Metale, półprzewodniki, izolatory
• Inny sposób wyrażenia tego samego:
Pierwiastki jednowartościowe
Sferyczne
y
powierzchnie
izoenergetyczne
24
Pierwiastki dwuwartościowe
Magnez ma 2 elektrony 3s Można by się
spodziewać, że pasmo 3s będzie
całkowicie zapełnione,
p
a 3pp całkowicie
puste. Mg powinien być izolatorem?
3p
3s
Ale magnez, Ca, Sr itp. Są metalami
Pasma 3s i 3p nakładają się i razem
tworzą częściowo zapełnione pasmo.
3p
3s
Metale dwuwartościowe: np. Mg
Pasmo przewodnictwa
p
Nie ma przerwy
Pasmo walencyjne
59
25
Metale przejściowe: np. Cu
Nakładają się na siebie pasma elektronów 4s i 3d.
Prawie sferyczne powierzchnie izoenergetyczne.
Półmetale
• Cięższe pierwiastki kolumny V układu okresowego: As,
Sb i Bi są półmetalami.
półmetalami Przez półmetal rozumiemy
metal o bardzo małej (w porównaniu z typowymi
metalami) gęstości stanów na powierzchni
Fermiego.
• Spośród pierwiastków układu okresowego półmetalem
jjest pponadto ggrafit,, najpowszechniejsza
jp
j
odmiana węgla.
ęg
Półmetaliczne przewodnictwo warunkuje szereg
zastosowań tego materiału (oporniki węglowe, elektrody
do baterii galwanicznych i pieców łukowych, szczotki do
silników i prądnic).
26